Lesson 11
Using Equations to Solve Problems
11.1: Remember Tape Diagrams (5 minutes)
Warm-up
The purpose of this warm-up is to reactivate students’ understanding of tape diagrams to make it more likely that tape diagrams are accessible as a tool for them to choose in this lesson. The diagram was deliberately constructed to encourage some students to write an equation like \(24=3(a+2)\) and others like \(24=3a+6\). Monitor for one student who writes each type of equation.
Launch
Arrange students in groups of 2. Give 5 minutes of quiet think time and time to share their work with a partner followed by a whole-class discussion.
Student Facing
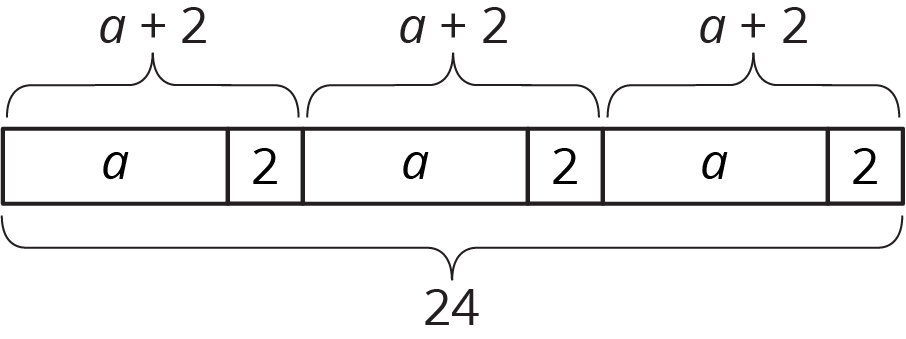
- Write a story that could be represented by this tape diagram.
- Write an equation that could be represented by this tape diagram.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
After students have had a chance to share their work with their partner, select a few students to share their stories. Then, select one student to share each type of equation and explain its structure: \(3(a+2)=24\) and \(3a+6=24\).
11.2: At the Fair (15 minutes)
Activity
In this activity, students use a tape diagram to help them reason about a situation, write an equation that represents it, and solve the equation. Students can use both the diagram and the solution strategy of doing the same to each side and undoing that they saw in the past few lessons. The first two questions provide more scaffolding and the last question provides none.
When students work on the last question, monitor for students who
- reason numerically without any diagrams or representations.
- create a tape diagram and use it to reason numerically.
- write an equation like \(6(x-1.5)=46.5\) and solve it by using the distributive property to find the total amount saved, \(6\boldcdot 1.50\).
- write an equation and solve it by first dividing by 6 to find the cost of each discounted ticket.
Launch
Keep students in the same groups. Give students 5–10 minutes of quiet work time and partner discussions followed by a whole-class discussion.
Supports accessibility for: Organization; Attention
Student Facing
- Tyler is making invitations to the fair. He has already made some of the invitations, and he wants to finish the rest of them within a week. He is trying to spread out the remaining work, to make the same number of invitations each day. Tyler draws a diagram to represent the situation.

-
Explain how each part of the situation is represented in Tyler’s diagram:
How many total invitations Tyler is trying to make.
How many invitations he has made already.
How many days he has to finish the invitations.
- How many invitations should Tyler make each day to finish his goal within a week? Explain or show your reasoning.
- Use Tyler’s diagram to write an equation that represents the situation. Explain how each part of the situation is represented in your equation.
- Show how to solve your equation.
-
-
Noah and his sister are making prize bags for a game at the fair. Noah is putting 7 pencil erasers in each bag. His sister is putting in some number of stickers. After filling 3 of the bags, they have used a total of 57 items.

- Explain how the diagram represents the situation.
- Noah writes the equation \(3(x+7) = 57\) to represent the situation. Do you agree with him? Explain your reasoning.
- How many stickers is Noah's sister putting in each prize bag? Explain or show your reasoning.
- A family of 6 is going to the fair. They have a coupon for $1.50 off each ticket. If they pay $46.50 for all their tickets, how much does a ticket cost without the coupon? Explain or show your reasoning. If you get stuck, consider drawing a diagram or writing an equation.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite selected students to share their strategies for the last problem, following the sequence of approaches in the Activity Narrative. As students present, display the different approaches side by side, and ask students to explain the meaning of the numbers they find.
Design Principle(s): Maximize meta-awareness; Support sense-making
11.3: Running Around (15 minutes)
Activity
This activity offers four word problems. Depending on time constraints, you may have all students complete all four problems or assign a different problem to each group. The problems increase in difficulty. It is suggested that students create a visual display of one of the problems and do a gallery walk or presentation, but if time is short, you may choose to just have students work in their workbooks or devices.
Launch
Keep students in the same groups. Either instruct students to complete all four problems or assign one problem to each group. If opting to have students do presentations or a gallery walk, distribute tools for making a visual display.
Give students 5–6 minutes quiet work time and a partner discussion followed by a whole-class discussion or gallery walk.
Supports accessibility for: Language; Conceptual processing
Student Facing
Priya, Han, and Elena, are members of the running club at school.
-
Priya was busy studying this week and ran 7 fewer miles than last week. She ran 9 times as far as Elena ran this week. Elena only had time to run 4 miles this week.
- How many miles did Priya run last week?
- Elena wrote the equation \(\frac19 (x-7) = 4\) to describe the situation. She solved the equation by multiplying each side by 9 and then adding 7 to each side. How does her solution compare to the way you found Priya's miles?
-
One day last week, 6 teachers joined \(\frac57\) of the members of the running club in an after-school run. Priya counted a total of 31 people running that day. How many members does the running club have?
-
Priya and Han plan a fundraiser for the running club. They begin with a balance of -80 because of expenses. In the first hour of the fundraiser they collect equal donations from 9 family members, which brings their balance to -44. How much did each parent give?
-
The running club uses the money they raised to pay for a trip to a canyon. At one point during a run in the canyon, the students are at an elevation of 128 feet. After descending at a rate of 50 feet per minute, they reach an elevation of -472 feet. How long did the descent take?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A musician performed at three local fairs. At the first he doubled his money and spent $30. At the second he tripled his money and spent $54. At the third, he quadrupled his money and spent $72. In the end he had $48 left. How much did he have before performing at the fairs?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
The phrases “9 times as far” and “9 times as many” may lead students to think about multiplying by 9 instead of dividing (or multiplying by \(\frac19\)). Encourage students to act out the situations or draw diagrams to help reason about the relationship between the quantities. Remind them to pay careful attention to what or who a comparison refers to.
Activity Synthesis
If students created a visual display and you opt to conduct a gallery walk, ask students to post their solutions. Distribute sticky notes and ask students to read others’ solutions, using the sticky notes to leave questions or comments. Give students a moment to review any questions or comments left on their display.
Invite any students who chose to draw a diagram to share; have the class agree or disagree with their diagrams and suggest any revisions. Next, invite students who did not try to draw a diagram to share strategies. Ask students about any difficulties they had creating the expressions and equations. Did the phrase “9 times as many” suggest an incorrect expression? If yes, how did they catch and correct for this error?
Lesson Synthesis
Lesson Synthesis
Ask students to reflect on the work done in this unit so far. What strategies have they learned? What kinds of problems can they solve that they weren’t able to, previously? Ask them to write down or share with a partner one new thing they have learned and one thing they still have questions or confusion about.
11.4: Cool-down - The Basketball Game (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Many problems can be solved by writing and solving an equation. Here is an example:
Clare ran 4 miles on Monday. Then for the next six days, she ran the same distance each day. She ran a total of 22 miles during the week. How many miles did she run on each of the 6 days?
One way to solve the problem is to represent the situation with an equation, \(4+6x = 22\), where \(x\) represents the distance, in miles, she ran on each of the 6 days. Solving the equation gives the solution to this problem.
\(\begin{align} 4+6x &= 22 \\ 6x &= 18 \\ x &= 3 \\ \end{align}\)