Lesson 8

Reasoning about Solving Equations (Part 2)

Let’s use hangers to understand two different ways of solving equations with parentheses.

8.1: Equivalent to $2(x+3)$

Select all the expressions equivalent to \(2(x+3)\).

  1. \(2 \boldcdot (x+3) \)
  2. \((x + 3)2 \)
  3. \(2 \boldcdot x + 2 \boldcdot 3\) 
  4. \(2 \boldcdot x + 3 \)
  5. \((2 \boldcdot x) + 3\) 
  6. \((2 + x)3\)

8.2: Either Or

  1. Explain why either of these equations could represent this hanger:

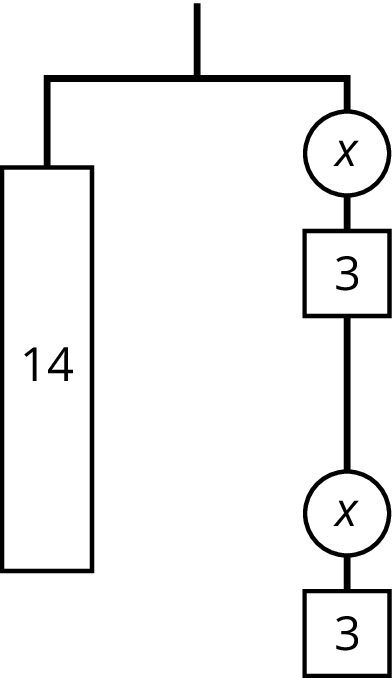
    Balanced hanger diagram, left side, rectangle 14, right side, circle x, square 3, circle x, square 3.

    \(14=2(x+3)\) or \(14=2x+6\)

  2. Find the weight of one circle. Be prepared to explain your reasoning.

8.3: Use Hangers to Understand Equation Solving, Again

Here are some balanced hangers. Each piece is labeled with its weight.

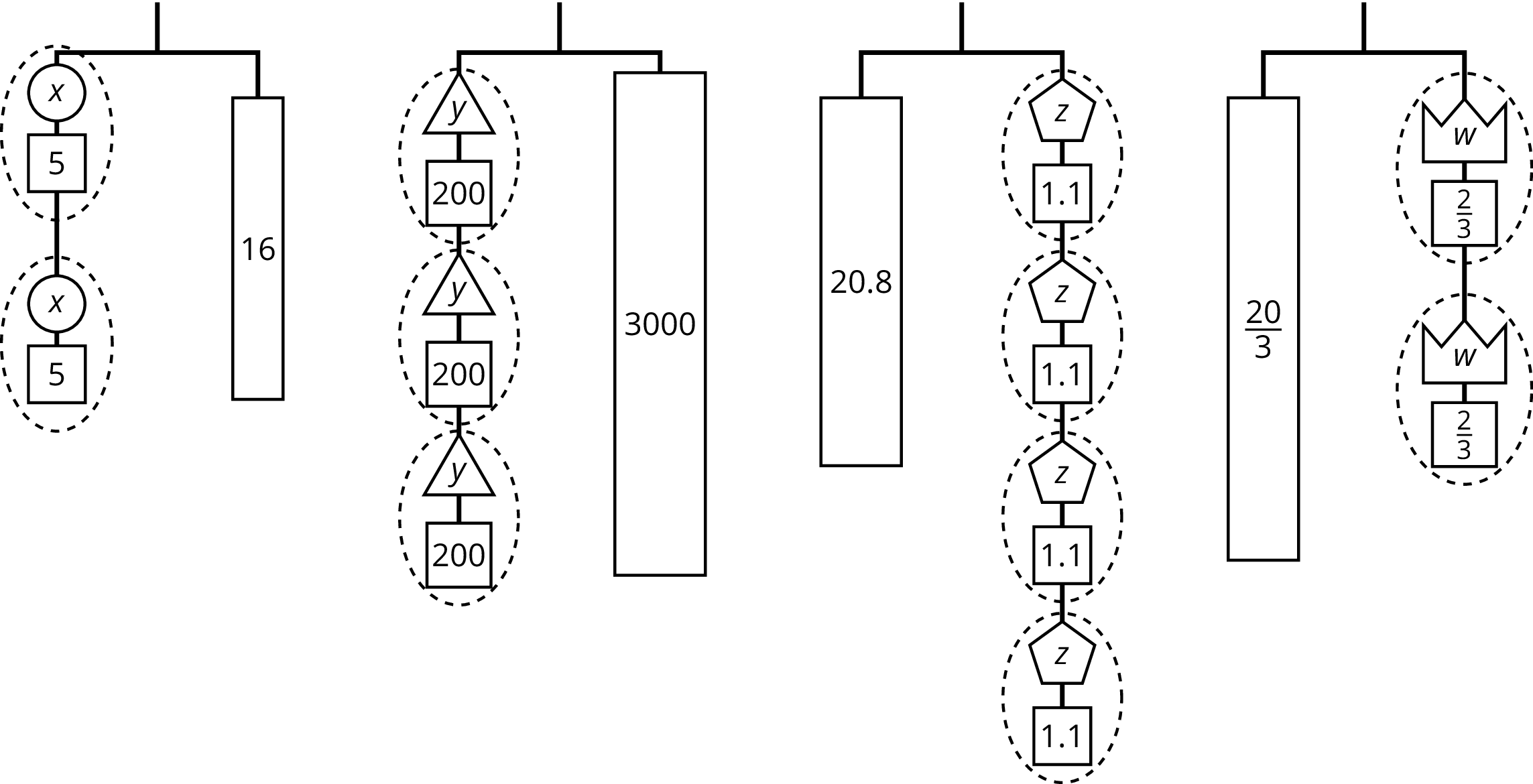
Four balanced hanger diagrams.

For each diagram:

  1. Assign one of these equations to each hanger: 

    \(2(x+5)=16\)

    \(3(y+200)=3\!,000\)

    \(20.8=4(z+1.1)\)

    \(\frac{20}{3}=2\left(w+\frac23\right)\)

  2. Explain how to figure out the weight of a piece labeled with a letter by reasoning about the diagram.
  3. Explain how to figure out the weight of a piece labeled with a letter by reasoning about the equation.

Summary

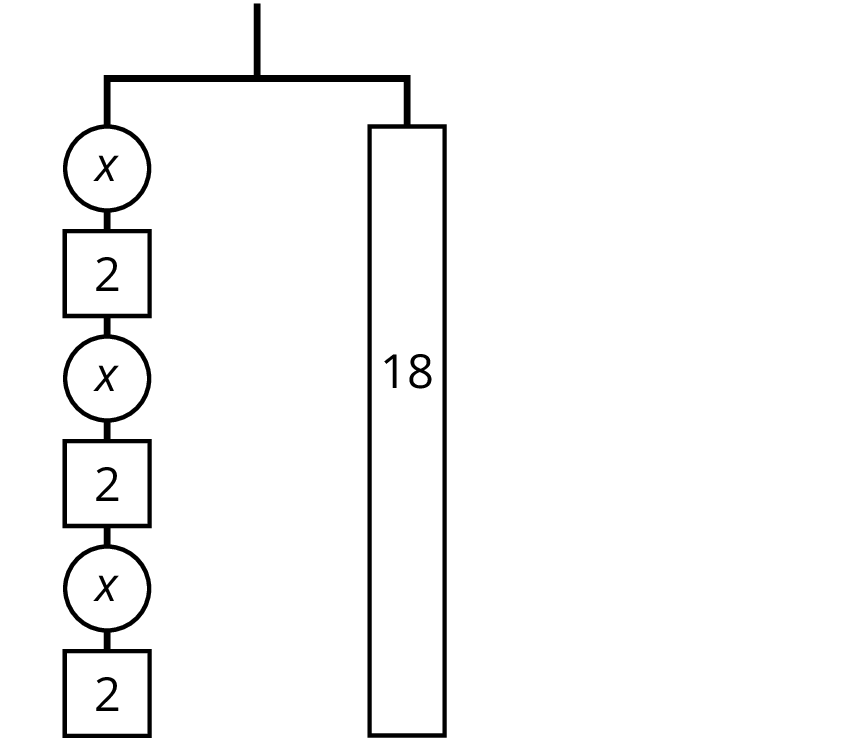
The balanced hanger shows 3 equal, unknown weights and 3 2-unit weights on the left and an 18-unit weight on the right.

There are 3 unknown weights plus 6 units of weight on the left. We could represent this balanced hanger with an equation and solve the equation the same way we did before.

\(\begin {align} 3x+6&=18 \\ 3x&=12 \\ x&=4 \\ \end{align}\)

Balanced hanger. Left side, circle labeled x, square labeled 2, circle labeled x, square labeled 2, circle labeled x, square labeled 2. Right side, rectangle labeled 18.

Since there are 3 groups of \(x+2\) on the left, we could represent this hanger with a different equation: \(3(x+2)=18\).

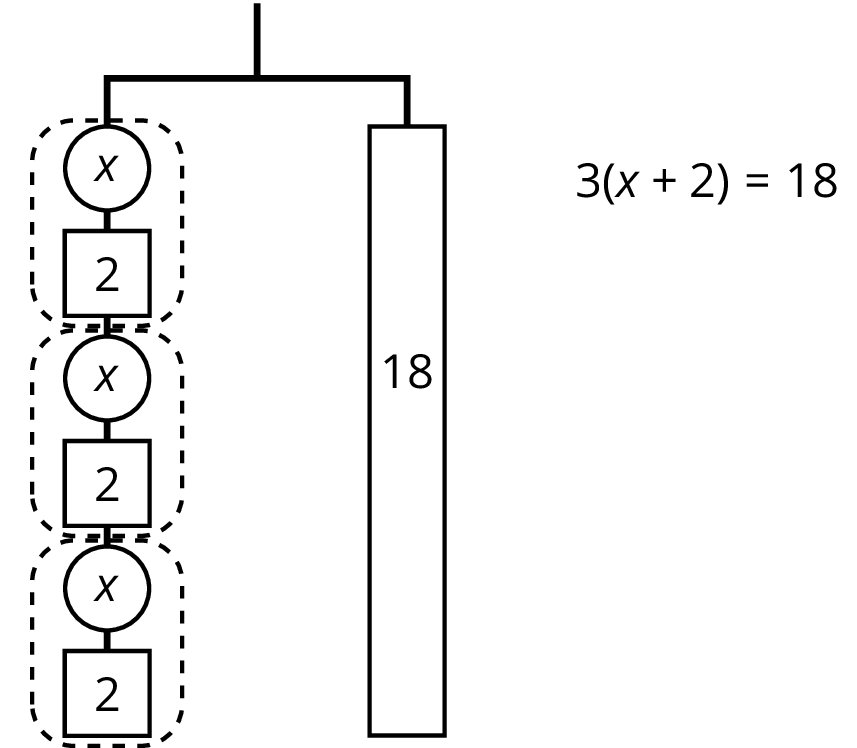
Balanced hanger, three groups are indicated, each group contains 1 circle labeled x and 1 square labeled 2. Right side, rectangle labeled 18.  To the side, an equation 3 ( x + 2 ) = 18.

The two sides of the hanger balance with these weights: 3 groups of \(x+2\) on one side, and 18, or 3 groups of 6, on the other side.

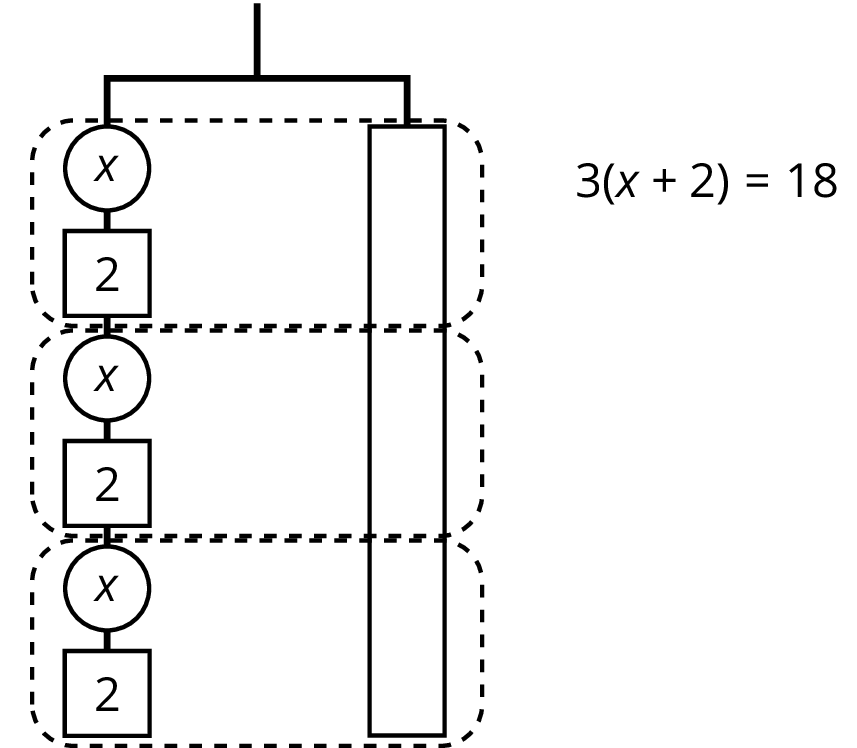
Balanced hanger. to the side, an equation.

The two sides of the hanger will balance with \(\frac13\) of the weight on each side: \(\frac13 \boldcdot 3(x+2) = \frac13 \boldcdot 18\).

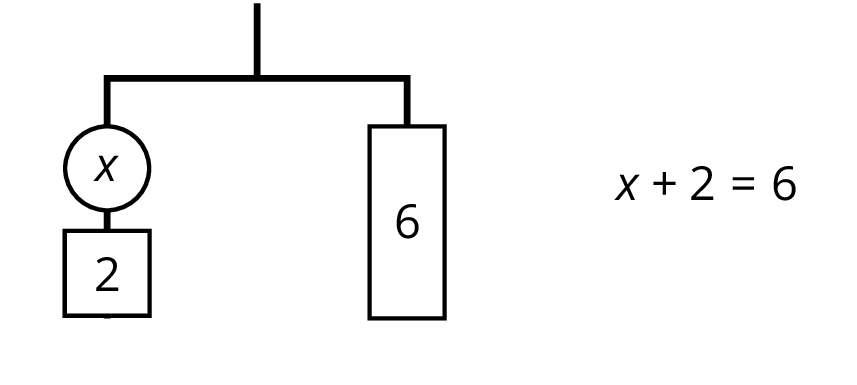
Balanced hanger, left side, 1 circle labeled x and 1 square labeled 2, right side, rectangle labeled 6.  To the side, an equation says x + 2 = 6.

We can remove 2 units of weight from each side, and the hanger will stay balanced. This is the same as subtracting 2 from each side of the equation.

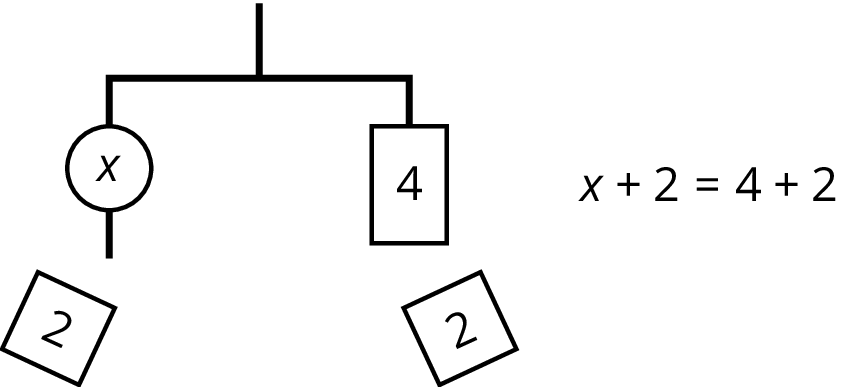
Balanced hanger.

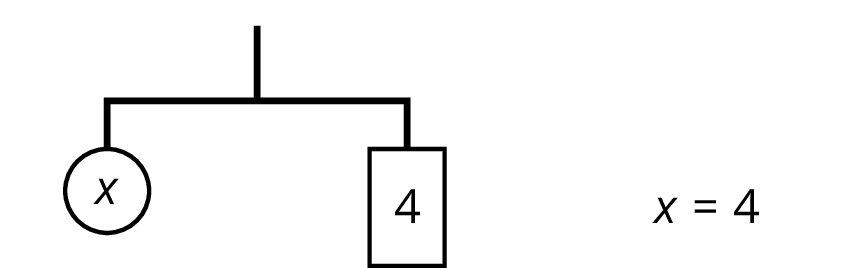
An equation for the new balanced hanger is \(x=4\). This gives the solution to the original equation.

Balanced hanger, left side, circle labeled x, right side, rectangle labeled 4. To the side, an equation x = 4.

Here is a concise way to write the steps above:

\(\begin{align} 3(x+2) &= 18 \\ x + 2 &= 6 & \text{after multiplying each side by } \tfrac13 \\ x &= 4 & \text{after subtracting 2 from each side} \\ \end{align} \)