Lesson 3
Reasoning about Equations with Tape Diagrams
3.1: Find Equivalent Expressions (10 minutes)
Warm-up
Students learned all about the distributive property in grade 6, including how to use the distributive property to rewrite expressions like \(6(2x-3)\) and \(12a+8a\). This is an opportunity for students to remember what the distributive property is all about before they will be expected to use it in the process of solving equations of the form \(p(x+q)=r\) later in this unit. If this activity indicates that students remember little of the distributive property from grade 6, heavier interventions may be needed.
Look for students who:
- Rule out expressions by testing values
- Use the term distributive property
Launch
Ask students to think of anything they know about equivalent expressions. Ask if they can:
- Explain why \(2x\) and \(2+x\) are not equivalent. (These expressions are equal when \(x\) is 2, but not equal for other values of \(x\). Multiplying 2 by a number usually gives a different result than adding that number to 2.)
- Explain why \(3+x\) and \(x+3\) are equivalent. (These expressions are equal no matter the value of \(x\). Also, addition is commutative.)
- Think of another example of two equivalent expressions. (Examples: \(2x\) and \(x \boldcdot 2\), \(a+a+a\), and \(3a\).)
- Explain what this term means. (Equivalent expressions are equal no matter the value assigned to the variable.)
- Describe ways to decide whether expressions are equivalent.
(Test some values, draw diagrams for different values, analyze them for properties of the operations involved.)
Arrange students in groups of 2. Give 3 minutes of quiet work time and then invite students to share their responses with their partner, followed by a whole-class discussion.
Student Facing
Select all the expressions that are equivalent to \(7(2-3n)\). Explain how you know each expression you select is equivalent.
- \(9-10n\)
- \(14-3n\)
- \(14-21n\)
- \((2-3n) \boldcdot 7\)
- \(7 \boldcdot 2 \boldcdot (\text- 3n)\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select a student who tested values to explain how they know two expressions are not equivalent. For example, \(9-10n\) is not equivalent to \(7(2-3n)\), because if we use 0 in place of \(n\), \(9-10\boldcdot0\) is 9 but \(7(2-3 \boldcdot n)\) is 14. If no one brings this up, demonstrate an example.
Select a student who used the term distributive property to explain why \(7(2-3n)\) is equivalent to \(14-21n\) to explain what they mean by that term. In general, an expression of the form \(a(b+c)\) is equivalent to \(ab+ac.\)
3.2: Matching Equations to Tape Diagrams (15 minutes)
Activity
In this activity, the tape diagrams and equations use the same numbers, so students must attend to the meaning of the operations in the equations and to the structure of the tape diagrams.
Look for students who have sensible ways to distinguish diagram A from diagram C, and also diagram D from diagram E. These correspond to using categories to sort the equations like “multiply by 2” vs. “multiply by 5.” Also look for students who categorize equations by “parentheses” vs. “no parentheses.” These categories correspond to distinguishing A, B, and C from D and E.
Launch
Keep students in the same groups. Tell them that, in this activity, they will match some diagrams, like the ones they saw in previous lessons, to corresponding equations. Then, they sort the list of equations into categories of their choosing. When they sort the equations, they should work with their partner to come up with categories, and then take turns sorting each equation into one of their categories, explaining why they are doing so. If necessary, demonstrate this protocol before students start working.
Give students 5 minutes to work with their partner followed by a whole-class discussion.
Supports accessibility for: Visual-spatial processing
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
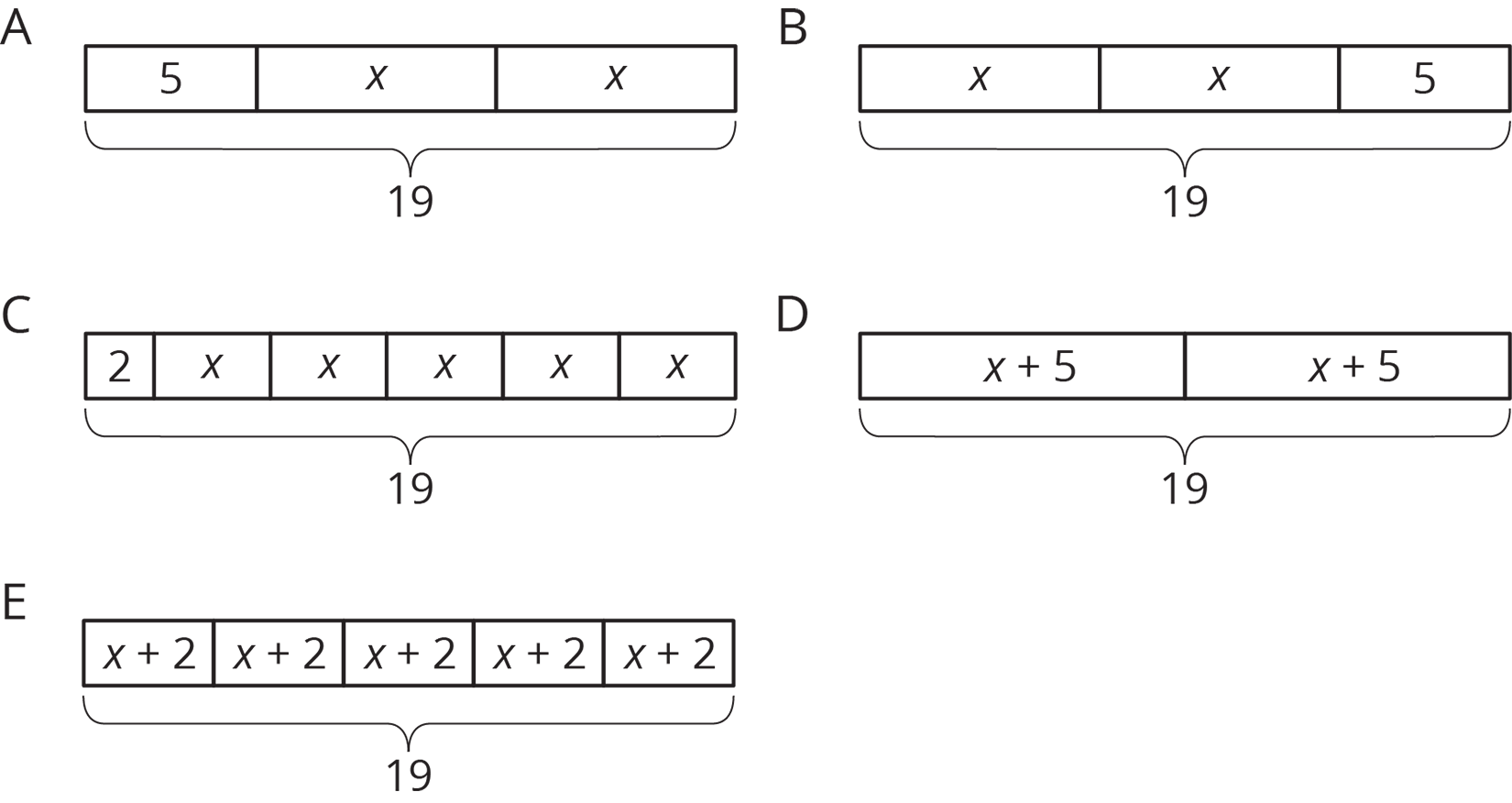
- Match each equation to one of the tape diagrams. Be prepared to explain how the equation matches the diagram.
- Sort the equations into categories of your choosing. Explain the criteria for each category.
- \(2x+5=19\)
- \(2+5x=19\)
- \(2(x+5)=19\)
- \(5(x+2)=19\)
- \(19=5+2x\)
- \((x+5) \boldcdot 2=19\)
- \(19=(x+2) \boldcdot 5\)
- \(19 \div 2 = x+5\)
- \(19-2=5x\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students don’t know where to begin, encourage them to describe the diagrams and equations in words. For example, diagram E could be described “two groups of \(x+5\) equal 19,” and so could the equation \(2(x+5)=19.\)
Activity Synthesis
Select a student who used the categories “multiply by 2” vs. “multiply by 5” to share their reasoning. Ask them to explain how we can see these categories in the corresponding diagrams. How did they categorize \(19 \div 2 = x+5\) which contains no multiplication?
Select a student to share their reasoning who used the categories “parentheses” vs. “no parentheses.” Did they have any misgivings about \(19 \div 2 = x+5\)? It contains no parentheses, but the corresponding diagram D also matches \(2(x+5)=19,\) which has parentheses.
If students express uncertainty about \(2x+5=19\), spend some time here. Some students are likely to match it to exactly one diagram and some students match it to both A and B. The point isn’t that one of these is right; it is to have the conversation about the idea of expressions or equations being identical vs. equivalent. Equivalent expressions or equivalent equations can have different literal interpretations, but when matching equations to tape diagrams, all that matters for the purposes of solving is that the equations are equivalent.
3.3: Drawing Tape Diagrams to Represent Equations (10 minutes)
Activity
This activity is parallel to one in the previous lesson, except that students are creating a tape diagram after interpreting an equation rather than interpreting a story. The intention is for students to reason in any way that makes sense to them about the equations and diagrams to figure out the solution to each equation. Do not demonstrate any equation solving procedures yet.
For each equation, monitor for a student who used their diagram to reason about a solution and a student who used the structure of the equation to reason about a solution.
Launch
Give students 5 minutes of quiet work time followed by a whole-class discussion.
Supports accessibility for: Conceptual processing; Memory
Design Principle(s): Support sense-making
Student Facing
-
Draw a tape diagram to match each equation.
- \(114 = 3x + 18\)
- \(114 = 3(y + 18)\)
-
Use any method to find values for \(x\) and \(y\) that make the equations true.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Give students 5 minutes of quiet work time followed by a whole-class discussion.
Supports accessibility for: Conceptual processing; Memory
Design Principle(s): Support sense-making
Student Facing
- \(114 = 3x + 18\)
- \(114 = 3(y + 18)\)
-
Draw a tape diagram to match each equation.
- Use any method to find values for \(x\) and \(y\) that make the equations true.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
To make a Koch snowflake:
- Start with an equilateral triangle that has side lengths of 1. This is step 1.
- Replace the middle third of each line segment with a small equilateral triangle with the middle third of the segment forming the base. This is step 2.
- Do the same to each of the line segments. This is step 3.
- Keep repeating this process.

- What is the perimeter after step 2? Step 3?
- What happens to the perimeter, or the length of line traced along the outside of the figure, as the process continues?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
For each equation, select a student who used their diagram to reason about a solution and a student who used the structure of the equation to reason about a solution. Ask these students to explain how they arrived at a solution. Display the diagram and the equation side by side as students are explaining, and draw connections between the two representations.
Do not demonstrate any equation-solving procedures yet.
Lesson Synthesis
Lesson Synthesis
Display one or more tape diagrams students encountered or created during the lesson, along with their corresponding equations. Ask, “What are some ways that tape diagrams represent equations?” Responses to highlight:
- Multiplication in the equation is represented with multiple copies of the same piece in the diagram.
- The total amount is shown in both the equation and the diagram.
- An unknown amount is represented with a variable.
- Either the equation or the diagram can be used to reason about a solution to the equation.
3.4: Cool-down - Three of These Equations Belong Together (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We have seen how tape diagrams represent relationships between quantities. Because of the meaning and properties of addition and multiplication, more than one equation can often be used to represent a single tape diagram.
Let’s take a look at two tape diagrams.
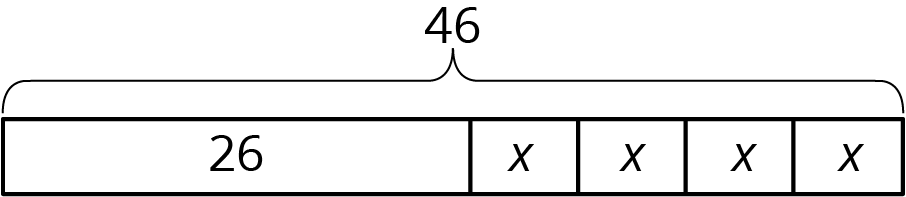
We can describe this diagram with several different equations. Here are some of them:
- \(26 + 4x=46\), because the parts add up to the whole.
- \(4x+26=46\), because addition is commutative.
- \(46=4x+26\), because if two quantities are equal, it doesn’t matter how we arrange them around the equal sign.
- \(4x=46-26\), because one part (the part made up of 4 \(x\)’s) is the difference between the whole and the other part.
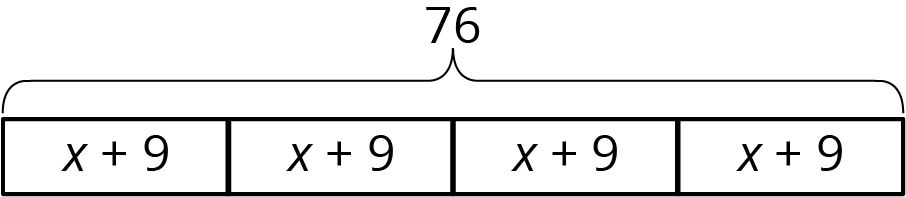
For this diagram:
- \(4(x+9)=76\), because multiplication means having multiple groups of the same size.
- \((x+9)\boldcdot 4=76\), because multiplication is commutative.
- \(76\div4=x+9\), because division tells us the size of each equal part.