Lesson 12
Solving Problems about Percent Increase or Decrease
12.1: 20% Off (10 minutes)
Warm-up
The purpose of this warm-up is for students to review how to solve for percentage change and represent these situations with expressions. Analyzing the structure of equivalent expressions for the same situation helps students see how the quantities in it are related. Since there are many equivalent expressions to represent how to find percentage change in a situation, encourage students to look for relationships between the expressions.
Launch
Arrange students in groups of 2. Give students 1 minute of quiet work time followed by 2 minutes to compare their responses with their partner. During the partner discussion, tell students to discuss the expressions they have in common, ones they don’t and then try to come to an agreement on the correct expressions that represent the price of the item after the discount. Follow with a whole-class discussion.
Student Facing
An item costs \(x\) dollars and then a 20% discount is applied. Select all the expressions that could represent the price of the item after the discount.
-
\(\frac{20}{100}x\)
-
\(x - \frac{20}{100}x\)
-
\(\left( 1-0.20 \right)x\)
-
\(\frac{100-20}{100}x\)
-
\(0.80x\)
-
\((100 - 20)x\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may choose expressions that represent the discount itself instead of the price of the item after the discount. Ask those students to refer back to the situation to identify which piece of the problem the expression they chose finds. If students are still unclear, it may be helpful to give students a price for \(x\) such as $10 and ask students if 20% of $10 makes sense as the new price of the item after the discount and then what piece of the problem they found.
Activity Synthesis
Ask students to indicate whether each expression represents the price of the item after the discount. If all students agree on an expression, ask 1 or 2 students to explain their reasoning and move to the next expression. Record and display their responses for all to see. If there is a disagreement on an expression, ask students to explain their reasoning for both choices and come to an agreement.
After the class had agreed on the four expressions that represent the price of the item after the discount, record them as a list and display them all to see. Ask students to discuss any connections they see between the expressions to show they are equivalent.
12.2: Walking More Each Day (10 minutes)
Activity
The first three questions help students recall how tape diagrams can be used to represent a percentage increase situation and draw connections to an equation representing percent increase. Monitor for different approaches in the first three questions (see solutions for different approaches).
The last question is review of previous work in this unit. This fourth question can be used for additional practice, but it can be safely skipped if time is short.
Launch
Keep students in the same groups. Tell students to work on the first three questions and pause for discussion. Give 5 minutes of quiet work time and time to share their responses with a partner, followed by a whole-class discussion. If time permits, the last question can be used as more practice on work from earlier in the unit.
Supports accessibility for: Memory; Organization
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
- Mai started a new exercise program. On the second day, she walked 5 minutes more than on the first day. On the third day, she increased her walking time from day 2 by 20% and walked for 42 minutes. Mai drew a diagram to show her progress.

- Noah said the equation \(1.20(d+5)=42\) also represents the situation. Do you agree with Noah? Explain your reasoning.
- Find the number of minutes Mai walked on the first day. Did you use the diagram, the equation, or another strategy? Explain or show your reasoning.
- Mai has been walking indoors because of cold temperatures. On Day 4 at noon, Mai hears a report that the temperature is only 9 degrees Fahrenheit. She remembers the morning news reporting that the temperature had doubled since midnight and was expected to rise 15 degrees by noon. Mai is pretty sure she can draw a diagram to represent this situation but isn't sure if the equation is \(9=15+2t\) or \(2(t+15)=9\). What would you tell Mai about the diagram and the equation and how they might be useful to find the temperature, \(t\), at midnight?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students bring up that the diagram represents 120% or \(\frac65\), or if they refer to each equal part as 20% or \(\frac15\), ask what whole the fraction or percent refers to. They should understand that the whole is the amount from Day 2, \(d+5\).
Activity Synthesis
Select groups with different approaches to share their responses to the first three questions.
12.3: A Sale on Shoes (15 minutes)
Activity
This activity offers four word problems. Depending on time constraints, you may have all students complete all four problems or assign a different problem to each group. The problems increase in difficulty. It is suggested that students create a visual display of one of the problems and do a gallery walk or presentation, but if time is short you may choose to just have students work in their workbooks or devices.
Launch
Keep students in the same groups. Either instruct students to complete all four problems or assign one problem to each group. If opting to have students do presentations or a gallery walk, distribute tools for making a visual display.
Give students 5–6 minutes quiet work time and partner discussion followed by a whole-class discussion or gallery walk.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
-
A store is having a sale where all shoes are discounted by 20%. Diego has a coupon for $3 off of the regular price for one pair of shoes. The store first applies the coupon and then takes 20% off of the reduced price. If Diego pays $18.40 for a pair of shoes, what was their original price before the sale and without the coupon?
-
Before the sale, the store had 100 pairs of flip flops in stock. After selling some, they notice that \(\frac35\) of the flip flops they have left are blue. If the store has 39 pairs of blue flip flops, how many pairs of flip flops (any color) have they sold?
-
When the store had sold \(\frac29\) of the boots that were on display, they brought out another 34 pairs from the stock room. If that gave them 174 pairs of boots out, how many pairs were on display originally?
-
On the morning of the sale, the store donated 50 pairs of shoes to a homeless shelter. Then they sold 64% of their remaining inventory during the sale. If the store had 288 pairs after the donation and the sale, how many pairs of shoes did they have at the start?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A coffee shop offers a special: 33% extra free or 33% off the regular price. Which offer is a better deal? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
If students created a visual display and you opt to conduct a gallery walk, ask students to post their solutions. Distribute sticky notes and ask students to read others’ solutions, using the sticky notes to leave questions or comments. Give students a moment to review any questions or comments left on their display.
Invite any students who chose to draw a diagram to share; have the class agree or disagree with their diagrams and suggest any revisions. Next, invite students who did not try to draw a diagram to share strategies. Ask students about any difficulties they had creating the expressions and equations. Highlight equivalent expressions that represent the same quantity and different strategies for solving equations.
Lesson Synthesis
Lesson Synthesis
Ask students to reflect on the work done in this unit so far. What strategies have they learned? What kinds of problems can they solve that they weren’t able to, previously? Ask them to write down or share with a partner one new thing they have learned and one thing they still have questions or confusion about.
12.4: Cool-down - Timing the Relay Race (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We can solve problems where there is a percent increase or decrease by using what we know about equations. For example, a camping store increases the price of a tent by 25%. A customer then uses a \$10 coupon for the tent and pays \$152.50. We can draw a diagram that shows first the 25% increase and then the \$10 coupon.
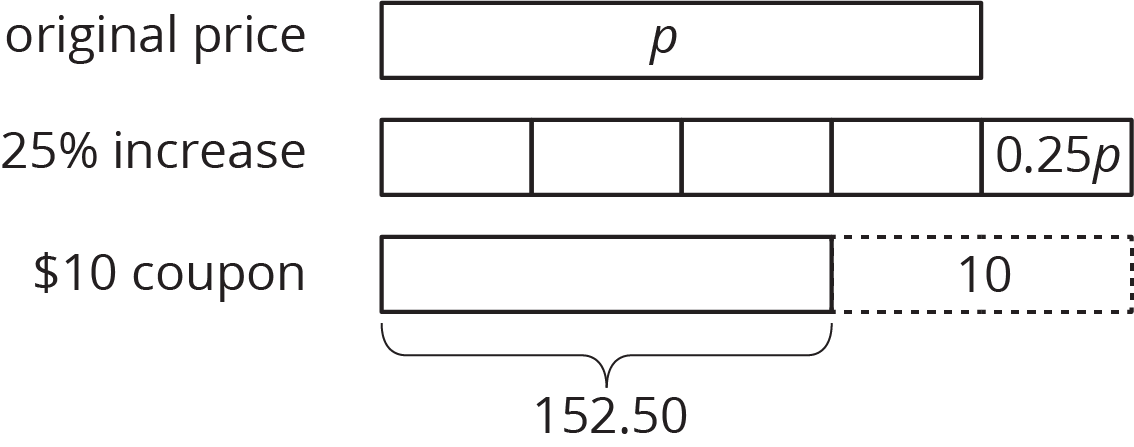
The price after the 25% increase is \(p+0.25p\) or \(1.25p\). An equation that represents the situation could be \(1.25p-10=152.50\). To find the original price before the increase and discount, we can add 10 to each side and divide each side by 1.25, resulting in \(p=130\). The original price of the tent was $130.