Lesson 4

Draw a square with side length 7 cm.

1. Predict the perimeter and the length of the diagonal of the square.
2. Measure the perimeter and the length of the diagonal of the square.
3. Describe how close the predictions and measurements are.

Find the products.

1. \((100) \boldcdot (\text-0.09)\)
2. \((\text-7) \boldcdot (\text- 1.1)\)
3. \((\text-7.3) \boldcdot (5)\)
4. \((\text-0.2)  \boldcdot (\text-0.3)\)

Here are three stories:

• A family buys 6 tickets to a show. They also pay a \$3 parking fee. They spend \$27 to see the show.

• Diego has 27 ounces of juice. He pours equal amounts for each of his 3 friends and has 6 ounces left for himself.

• Jada works for 6 hours preparing for the art fair. She spends 3 hours on a sculpture and then paints 27 picture frames.

Here is a diagram and its corresponding equation. Find the solution to the equation and explain your reasoning.

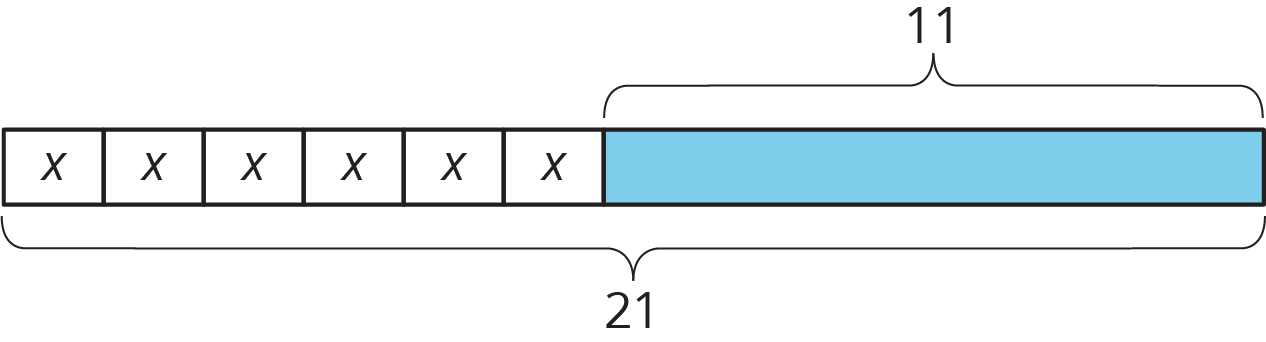
\(6x+11=21\)

1. Plot these points on the coordinate plane:

   \(A= (3, 2), B= (7.5, 2), C= (7.5, \text-2.5), D= (3, \text-2)\)

   

   

2. What is the vertical difference between \(D\) and \(A\)?
3. Write an expression that represents the vertical distance between \(B\) and \(C\).