Lesson 14

Finding Solutions to Inequalities in Context

View Student Lesson

Problem 1

The solution to \(5-3x > 35\) is either \(x>\text-10\) or \(\text-10>x\). Which solution is correct? Explain how you know.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

The school band director determined from past experience that if they charge \(t\) dollars for a ticket to the concert, they can expect attendance of \(1000-50t\). The director used this model to figure out that the ticket price needs to be $8 or greater in order for at least 600 to attend. Do you agree with this claim? Why or why not?

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Which inequality is true when the value of \(x\) is -3?

A:

\(\text-x -6 < \text-3.5\)

B:

\(\text-x- 6 >3.5\)

C:

\(\text-x -6 > \text-3.5\)

D:

\(x -6 > \text-3.5\)

Solution

For access, consult one of our IM Certified Partners.

(From Unit 6, Lesson 13.)

Problem 4

Draw the solution set for each of the following inequalities.

  1. \(x\leq5\)

    A number line with the numbers negative 10 through 9 indicated.

  2. \(x<\frac52\)

    A number line with the numbers negative 10 through 9 indicated.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 6, Lesson 13.)

Problem 5

Write three different equations that match the tape diagram.

Tape diagram, 1 part labeled 19, 7 equal parts lableled x, total 40.

 

Solution

For access, consult one of our IM Certified Partners.

(From Unit 6, Lesson 3.)

Problem 6

A baker wants to reduce the amount of sugar in his cake recipes. He decides to reduce the amount used in 1 cake by \(\frac12\) cup. He then uses \(4\frac12\) cups of sugar to bake 6 cakes.

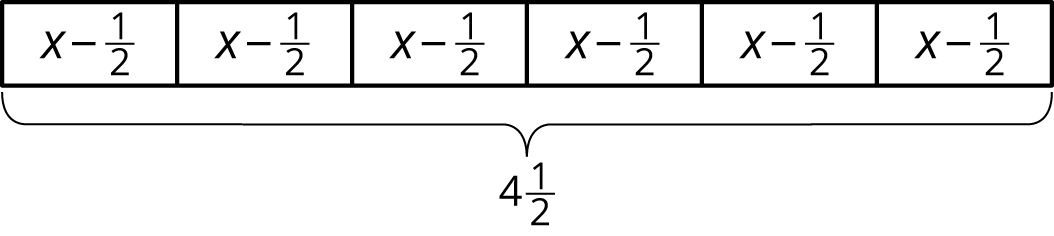
Tape diagram, 6 parts each labeled x minus 1 over 2, total 4 and 1 over 2.
  1. Describe how the tape diagram represents the story.
  2. How much sugar was originally in each cake recipe?

Solution

For access, consult one of our IM Certified Partners.

(From Unit 6, Lesson 2.)

Problem 7

One year ago, Clare was 4 feet 6 inches tall. Now Clare is 4 feet 10 inches tall. By what percentage did Clare’s height increase in the last year?

Solution

For access, consult one of our IM Certified Partners.

(From Unit 4, Lesson 12.)