Lesson 13

The number line shows values of \(x\) that make the inequality \(x>1\) true.

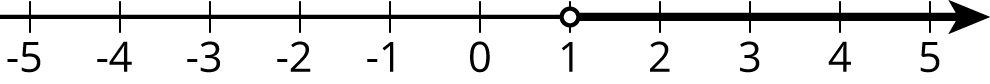
1. Select all the values of \(x\) from this list that make the inequality \(x>1\) true.

   1. 3

   2. -3

   3. 1

   4. 700

   5. 1.05

2. Name two more values of \(x\) that are solutions to the inequality.

1. Noah is \(x\) inches tall. Which of the following can be true: \(x > 60\), \(x = 60\), or \(x < 60\)? Explain how you know.
2. Noah’s friend is 2 inches shorter than Noah. Can you tell if Noah’s friend is tall enough to go on the ride? Explain or show your reasoning.
3. List one possible height for Noah that means that his friend is tall enough to go on the ride, and another that means that his friend is too short for the ride.

4. On the number line below, show all the possible heights that Noah’s friend could be.

   

   

5. Noah's friend is \(y\) inches tall. Use \(y\) and any of the symbols \(<\), \(=\), \(>\) to express this height.

The table shows four inequalities and four possible values for \(x\). Decide whether each value makes each inequality true, and complete the table with “true” or “false.” Discuss your thinking with your partner. If you disagree, work to reach an agreement.

\(x\)	0	100	-100	25
\(x \leq 25\)
\(100 < 4x\)
\(\text-3x > \text-75\)
\(10 \geq 35 - x\)

We use inequalities to describe a range of numbers. In many places, you are allowed to get a driver’s license when you are at least 16 years old. When checking if someone is old enough to get a license, we want to know if their age is at least 16. If \(h\) is the age of a person, then we can check if they are allowed to get a driver’s license by checking if their age makes the inequality \(h>16\) (they are older than 16) or the equation \(h=16\) (they are 16) true. The symbol \(\geq\), pronounced “greater than or equal to,” combines these two cases and we can just check if \(h \geq 16\) (their age is greater than or equal to 16). The inequality \(h \geq 16\) can be represented on a number line: