Lesson 12
Solving Problems about Percent Increase or Decrease
Let’s use tape diagrams, equations, and reasoning to solve problems with negatives and percents.
12.1: 20% Off
An item costs \(x\) dollars and then a 20% discount is applied. Select all the expressions that could represent the price of the item after the discount.
-
\(\frac{20}{100}x\)
-
\(x - \frac{20}{100}x\)
-
\(\left( 1-0.20 \right)x\)
-
\(\frac{100-20}{100}x\)
-
\(0.80x\)
-
\((100 - 20)x\)
12.2: Walking More Each Day
- Mai started a new exercise program. On the second day, she walked 5 minutes more than on the first day. On the third day, she increased her walking time from day 2 by 20% and walked for 42 minutes. Mai drew a diagram to show her progress.
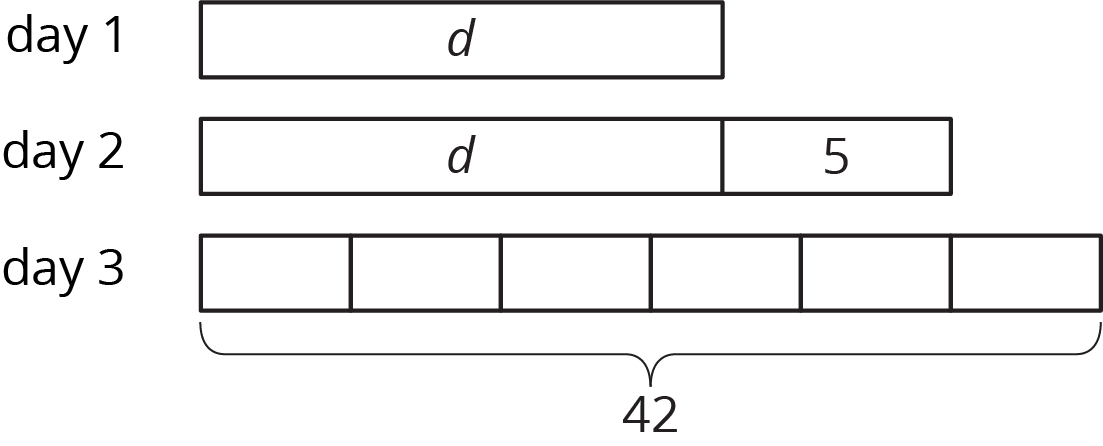
- Noah said the equation \(1.20(d+5)=42\) also represents the situation. Do you agree with Noah? Explain your reasoning.
- Find the number of minutes Mai walked on the first day. Did you use the diagram, the equation, or another strategy? Explain or show your reasoning.
- Mai has been walking indoors because of cold temperatures. On Day 4 at noon, Mai hears a report that the temperature is only 9 degrees Fahrenheit. She remembers the morning news reporting that the temperature had doubled since midnight and was expected to rise 15 degrees by noon. Mai is pretty sure she can draw a diagram to represent this situation but isn't sure if the equation is \(9=15+2t\) or \(2(t+15)=9\). What would you tell Mai about the diagram and the equation and how they might be useful to find the temperature, \(t\), at midnight?
12.3: A Sale on Shoes
-
A store is having a sale where all shoes are discounted by 20%. Diego has a coupon for $3 off of the regular price for one pair of shoes. The store first applies the coupon and then takes 20% off of the reduced price. If Diego pays $18.40 for a pair of shoes, what was their original price before the sale and without the coupon?
-
Before the sale, the store had 100 pairs of flip flops in stock. After selling some, they notice that \(\frac35\) of the flip flops they have left are blue. If the store has 39 pairs of blue flip flops, how many pairs of flip flops (any color) have they sold?
-
When the store had sold \(\frac29\) of the boots that were on display, they brought out another 34 pairs from the stock room. If that gave them 174 pairs of boots out, how many pairs were on display originally?
-
On the morning of the sale, the store donated 50 pairs of shoes to a homeless shelter. Then they sold 64% of their remaining inventory during the sale. If the store had 288 pairs after the donation and the sale, how many pairs of shoes did they have at the start?
A coffee shop offers a special: 33% extra free or 33% off the regular price. Which offer is a better deal? Explain your reasoning.
Summary
We can solve problems where there is a percent increase or decrease by using what we know about equations. For example, a camping store increases the price of a tent by 25%. A customer then uses a \$10 coupon for the tent and pays \$152.50. We can draw a diagram that shows first the 25% increase and then the \$10 coupon.

The price after the 25% increase is \(p+0.25p\) or \(1.25p\). An equation that represents the situation could be \(1.25p-10=152.50\). To find the original price before the increase and discount, we can add 10 to each side and divide each side by 1.25, resulting in \(p=130\). The original price of the tent was $130.