Lesson 11
Using Equations to Solve Problems
Let’s use tape diagrams, equations, and reasoning to solve problems.
11.1: Remember Tape Diagrams
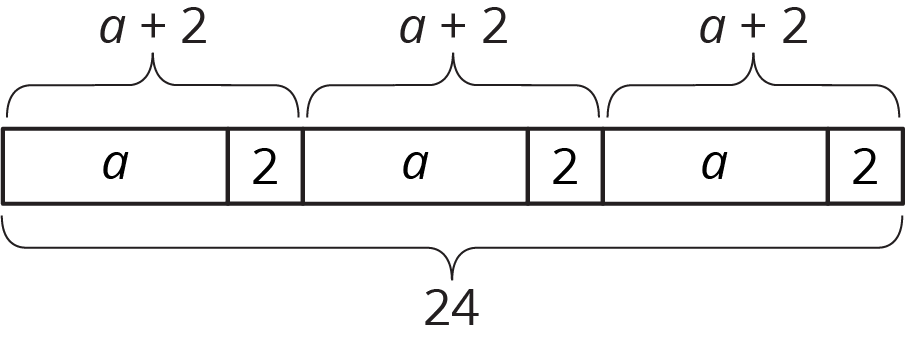
- Write a story that could be represented by this tape diagram.
- Write an equation that could be represented by this tape diagram.
11.2: At the Fair
- Tyler is making invitations to the fair. He has already made some of the invitations, and he wants to finish the rest of them within a week. He is trying to spread out the remaining work, to make the same number of invitations each day. Tyler draws a diagram to represent the situation.

-
Explain how each part of the situation is represented in Tyler’s diagram:
How many total invitations Tyler is trying to make.
How many invitations he has made already.
How many days he has to finish the invitations.
- How many invitations should Tyler make each day to finish his goal within a week? Explain or show your reasoning.
- Use Tyler’s diagram to write an equation that represents the situation. Explain how each part of the situation is represented in your equation.
- Show how to solve your equation.
-
-
Noah and his sister are making prize bags for a game at the fair. Noah is putting 7 pencil erasers in each bag. His sister is putting in some number of stickers. After filling 3 of the bags, they have used a total of 57 items.

- Explain how the diagram represents the situation.
- Noah writes the equation \(3(x+7) = 57\) to represent the situation. Do you agree with him? Explain your reasoning.
- How many stickers is Noah's sister putting in each prize bag? Explain or show your reasoning.
- A family of 6 is going to the fair. They have a coupon for $1.50 off each ticket. If they pay $46.50 for all their tickets, how much does a ticket cost without the coupon? Explain or show your reasoning. If you get stuck, consider drawing a diagram or writing an equation.
11.3: Running Around
Priya, Han, and Elena, are members of the running club at school.
-
Priya was busy studying this week and ran 7 fewer miles than last week. She ran 9 times as far as Elena ran this week. Elena only had time to run 4 miles this week.
- How many miles did Priya run last week?
- Elena wrote the equation \(\frac19 (x-7) = 4\) to describe the situation. She solved the equation by multiplying each side by 9 and then adding 7 to each side. How does her solution compare to the way you found Priya's miles?
-
One day last week, 6 teachers joined \(\frac57\) of the members of the running club in an after-school run. Priya counted a total of 31 people running that day. How many members does the running club have?
-
Priya and Han plan a fundraiser for the running club. They begin with a balance of -80 because of expenses. In the first hour of the fundraiser they collect equal donations from 9 family members, which brings their balance to -44. How much did each parent give?
-
The running club uses the money they raised to pay for a trip to a canyon. At one point during a run in the canyon, the students are at an elevation of 128 feet. After descending at a rate of 50 feet per minute, they reach an elevation of -472 feet. How long did the descent take?
A musician performed at three local fairs. At the first he doubled his money and spent $30. At the second he tripled his money and spent $54. At the third, he quadrupled his money and spent $72. In the end he had $48 left. How much did he have before performing at the fairs?
Summary
Many problems can be solved by writing and solving an equation. Here is an example:
Clare ran 4 miles on Monday. Then for the next six days, she ran the same distance each day. She ran a total of 22 miles during the week. How many miles did she run on each of the 6 days?
One way to solve the problem is to represent the situation with an equation, \(4+6x = 22\), where \(x\) represents the distance, in miles, she ran on each of the 6 days. Solving the equation gives the solution to this problem.
\(\begin{align} 4+6x &= 22 \\ 6x &= 18 \\ x &= 3 \\ \end{align}\)