Lesson 4
Half as Much Again
Lesson Narrative
In this lesson students see how to use the distributive property to write a compact expression for situations where one quantity is described in relation to another quantity in language such as "half as much again" and "one third more than." If \(y\) is half as much again as \(x\), then \(y = x + \frac12 x\). Using the distributive property, this can be written as \(y = (1 \frac12)x\). Students apply this sort of reasoning to various situations. A warm-up activity activates their prior knowledge of using the distributive property to write equivalent expressions. When students look for opportunities to use the distributive property to write equations in a simpler way, they are engaging in MP7.
In the next lesson they will consider similar situations involving fractions expressed as decimals. These two lessons prepare them for later study of situations involving percent increase and percent decrease.
Learning Goals
Teacher Facing
- Apply the distributive property to generate algebraic expressions that represent a situation involving adding or subtracting a fraction of the initial value, and explain (orally) the reasoning.
- Coordinate tables, equations, tape diagrams, and verbal descriptions that represent a relationship involving adding or subtracting a fraction of the initial value.
- Generalize a process for finding the value that is “half as much again,” and justify (orally and in writing) why this can be abstracted as $\frac32 x$ or equivalent.
Student Facing
Let’s use fractions to describe increases and decreases.
Required Preparation
Print and cut up slips from the Representations of Proportional Relationships Card Sort blackline master. Prepare 1 copy for every 2 students. These can be re-used if you have more than one class. Consider making a few extra copies that are not cut up to serve as an answer key.
Learning Targets
Student Facing
- I can use the distributive property to rewrite an expression like $x+\frac12 x$ as $(1+\frac12)x$.
- I understand that “half as much again” and “multiply by $\frac32$” mean the same thing.
CCSS Standards
Glossary Entries
-
tape diagram
A tape diagram is a group of rectangles put together to represent a relationship between quantities.
For example, this tape diagram shows a ratio of 30 gallons of yellow paint to 50 gallons of blue paint.
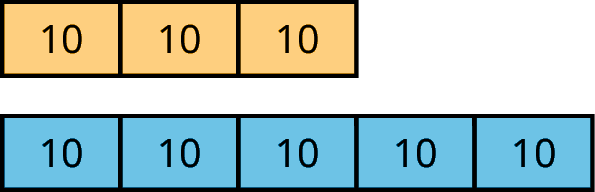
If each rectangle were labeled 5, instead of 10, then the same picture could represent the equivalent ratio of 15 gallons of yellow paint to 25 gallons of blue paint.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |