Lesson 13
Measurement Error
13.1: Measuring to the Nearest (10 minutes)
Warm-up
The purpose of this task is to notice how differences in recorded measurements can result from the level of precision of your measuring device. Students use rulers that have varying levels of accuracy to measure the same lines. This warm-up gets the conversation started around measurement error that will continue in the follow activities.
Students will need to use the rulers again later in this lesson, so make sure they keep track of them.
Launch
Arrange students in groups of 2. Give each group one copy of the blackline master and access to scissors or cut out the rulers provided ahead of time. Remind students that they are to use the two different rulers to measure the line segments.
Give students 3–5 minutes of quiet work time to complete the task with their partner. Follow with whole-class discussion.
Student Facing
Your teacher will give you two rulers and three line segments labeled A, B, and C.
- Use the centimeter ruler to measure each line segment to the nearest centimeter. Record these lengths in the first column of the table.
- Use the millimeter ruler to measure each line segment to the nearest tenth of a centimeter. Record these lengths in the second column of the table.
| line segment | length (cm) as measured with the first ruler |
length (cm) as measured with the second ruler |
|---|---|---|
| A | ||
| B | ||
| C |
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might not line up the edge of the ruler with the end of the line. Remind students that we need to line up the 0 mark on the ruler (in this case, the edge of the ruler) with the beginning edge of the line being measured.
Activity Synthesis
Ask students if they noticed anything between the lengths they got using the two different measuring devices (resulted in different recorded measurements). Explain to students that measurement error can result from the precision level of your measuring device. Ask students, “Assuming the measurements to the nearest tenth are exact, by how much was each measurement in error when you used the centimeter scaled ruler?” (7 cm was 0.3 cm too long, 0.1 cm too long, and 0.3 cm too short respectively.)
13.2: Measuring a Soccer Field (10 minutes)
Activity
In the warm-up, students learned that measurement error can result from the level of precision in a measuring device. In this activity, students learn about how real-world limitations on humans using measuring devices can introduce measurement errors. They discuss possible sources of error and express the error both as an amount and as a percentage. This is their first introduction into the concept of measurement error and how we use that to calculate percent error.
Launch
Keep students in groups of 2. Tell students that a soccer field is 120 yards long and ask them how they can measure that length using a 30-foot-long tape measure. (Note the use of two different units of measure, here.) If not mentioned by students, suggest measuring off 30 feet, making a mark, measuring off another 30 feet, and so on. Ask the class if they would all get exactly the same answer by this method. Tell students they are going to think more deeply about a specific measurement made by a person. Give the students 1–2 minutes of quiet work time to calculate the amount of the error and the percent error followed by partner and whole-group discussions.
Student Facing
A soccer field is 120 yards long. Han measures the length of the field using a 30-foot-long tape measure and gets a measurement of 358 feet, 10 inches.
-
What is the amount of the error?
- Express the error as a percentage of the actual length of the field.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students fail to see the need for converting units of measure, ask them how many feet are in 120 yards? How many inches?
Activity Synthesis
Ask students, "What is a possible cause of the error?" Possible reasons include:
- He did not position the tape measure precisely every time he measured another 30 feet.
- He didn't go in a completely straight line. (Although this would result in a longer measurement.)
- Han did not correctly use the measuring tape.
Ask a few students to share their solutions for the last problem.
Explain to students, measurement error is the positive difference between the measurement and the actual value. The percent error is the error expressed as a percentage of the actual value. We always use a positive number to express percent error and, when appropriate, use words to describe whether the measurement is greater than or less than the actual value. In this case, we might say that the measured length was less than the actual length with a percent error of 0.32%.
Ask, "When might percent error be more useful than measurement error?" If needed, give an example of measuring a student's height and being incorrect by an inch versus measuring the height of a skyscraper and being incorrect by an inch. Although the measurement error is the same (1 inch), the percent error is very different since the 1 inch difference is significantly more important when measuring shorter distances.
Supports accessibility for: Memory; Language
Design Principle(s): Maximize meta-awareness
13.3: Measuring Your Classroom (20 minutes)
Activity
This activity has students measuring things around the classroom to connect to the previous activity about measurement error. Students will work with their partner to measure 3 different things found in the classroom that the teacher has measured ahead of time (to obtain an “actual” measurement). They will use two different rulers (one with mm markings and one without).
After both students in a group have measured their three objects, provide them with the actual measurements of those items. They will calculate the measurement and percent errors after given the actual measurements.
Monitor for students who develop different procedures for computing percent error. For example: describing an algorithm in words (verbally or in writing), describing an algorithm more symbolically like \(\dfrac{|\text{actual}-\text{measured}|}{\text{actual}}\), or constructing a table of values.
Also monitor for a group whose two tables clearly shows how using the less-precise ruler results in greater percent error.
Launch
Keep students in the same groups of 2. Students will need the two rulers from the blackline master from the warm-up of this lesson.
Assign each group 3 objects to measure (that you have measured ahead of time). If possible, select some items that are longer than the rulers provided so that students may encounter the issue raised in the previous activity.
Tell students that they will fill in only the first 2 columns of each table using their rulers to measure. After groups have completed measuring their 3 objects, tell students the measurements you made of these same objects for them to fill in the third column of the tables. Students should then work to fill in the last 2 columns of the table.
Give students 3–5 minutes of quiet work time and then allow time for them to discuss with a partner, followed by whole-class discussion.
Supports accessibility for: Organization; Attention
Student Facing
Your teacher will tell you which three items to measure. Keep using the paper rulers from the earlier activity.
- Between you and your partner, decide who will use which ruler.
-
Measure the three items assigned by your teacher and record your measurements in the first column of the appropriate table.
Using the cm ruler:
item measured
length (cm)actual
length (cm)difference percentage Using the mm ruler:
item measured
length (cm)actual
length (cm)difference percentage - After you finish measuring the items, share your data with your partner. Next, ask your teacher for the actual lengths.
- Calculate the difference between your measurements and the actual lengths in both tables.
- For each difference, what percentage of the actual length is this amount? Record your answers in the last column of the tables.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Before there were standard units of measurement, people often measured things using their hands or feet.
- Measure the length of your foot to the nearest centimeter with your shoe on.
- How many foot-lengths long is your classroom? Try to determine this as precisely as possible by carefully placing your heel next to your toe as you pace off the room.
- Use this information to estimate the length of your classroom in centimeters.
- Use a tape measure to measure the length of your classroom. What is the difference between the two measurements? Which one do you think is more accurate?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
There are two desired outcomes of this activity: to develop a procedure that makes sense to students for computing percent error, and to reinforce that less-precise measuring devices result in greater percent error.
Select a few students who came up with different, correct procedures for computing percent error to explain their reasoning. A procedure might be described like, “Find the difference between the measured length and the actual length. Divide this difference by the actual length. Express the result as a percentage.” Other procedures may also be appropriate. For example, students might construct a table of values or a double number line to help them reason about expressing the error as a percentage of the actual length.
To highlight the effects of using a less-precise measuring device, select a pair of students whose tables clearly show that the measurements taken with the centimeter ruler had greater percent error than the measurements taken with the millimeter ruler. Display their work and ask them to explain why the measurements taken with the centimeter ruler had greater percent error.
Design Principle(s): Support sense-making; Cultivate conversation
Lesson Synthesis
Lesson Synthesis
Students should have a basic understanding of what measurement error is and how to use it to calculate percent error. Ask students:
- “What is measurement error? What causes measurement error?” (The difference between a measurement of an object and it's actual measure. It may exist due to human error in using a measurement tool or because the tool itself is not precise.)
- “How can we minimize the amount of error?” (Use precision tools and care when using them.)
- “What is the relationship between measurement error and percent error?” (Percent error is the measurement error divided by the actual quantity.)
13.4: Cool-down - Off by a Little Bit? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
When we are measuring a length using a ruler or measuring tape, we can get a measurement that is different from the actual length. This could be because we positioned the ruler incorrectly, or it could be because the ruler is not very precise. There is always at least a small difference between the actual length and a measured length, even if it is a microscopic difference!
Here are two rulers with different markings.
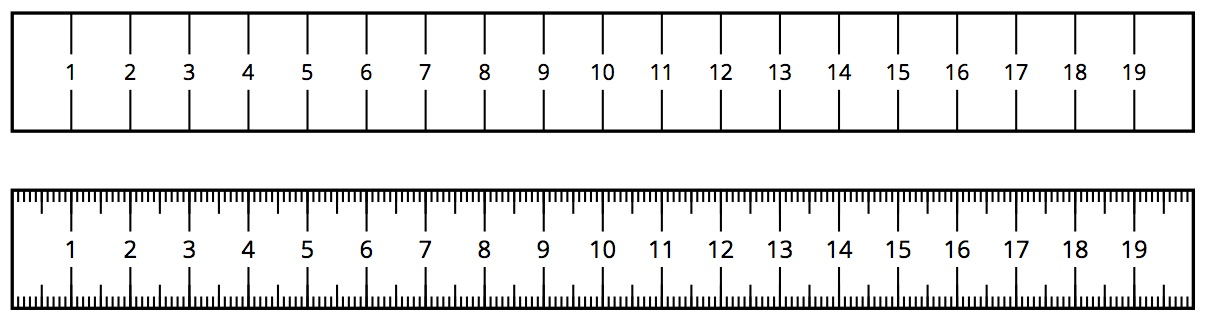
The second ruler is marked in millimeters, so it is easier to get a measurement to the nearest tenth of a centimeter with this ruler than with the first. For example, a line that is actually 6.2 cm long might be measured to be 6 cm long by the first ruler, because we measure to the nearest centimeter.
The measurement error is the positive difference between the measurement and the actual value. Measurement error is often expressed as a percentage of the actual value. We always use a positive number to express measurement error and, when appropriate, use words to describe whether the measurement is greater than or less than the actual value.
For example, if we get 6 cm when we measure a line that is actually 6.2 cm long, then the measurement error is 0.2 cm, or about 3.2%, because \(0.2 \div 6.2 \approx 0.032\).