Lesson 3
Revisiting Proportional Relationships
3.1: Recipe Ratios (5 minutes)
Warm-up
The purpose of this warm-up is to bring up two main methods for figuring out missing numbers in a table that represents a proportional relationship. The two methods students might use for this activity are:
- Using a scale factor to find equivalent ratios, e.g. multiplying the first row by \(1 \frac12\) to get the second row.
- Using the constant of proportionality, 2, between the first column and the second column.
This activity is to get students thinking about the second method as a more efficient method, since it works for every row. This lays the groundwork for solving problems using proportional relationships and for the activities in this lesson (specifically, the activity right after the warm up).
Launch
In a previous unit, students worked extensively with sets of equivalent ratios that represented ingredients for different numbers of batches of a recipe. If necessary, remind them how this works. For example, you might say "This recipe calls for \(\frac12\) cup of sugar and 1 cup of flour. What if I wanted to make half a batch of the recipe? What if I wanted to make 5 batches?"
Arrange students in groups of 2. Give 1 minute of quiet work time followed by time to compare their table with a partner and a whole-class discussion.
Student Facing
A recipe calls for \(\frac12\) cup sugar and 1 cup flour. Complete the table to show how much sugar and flour to use in different numbers of batches of the recipe.
| sugar (cups) | flour (cups) |
|---|---|
| \(\frac12\) | 1 |
| \(\frac34\) | |
| \(1\frac34\) | |
| 1 | |
| \(2\frac12\) |
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may assume the sugar column will continue to increase by the same amount without paying close attention to the values in the flour column. Ask these students what they notice about the values in the flour column and if it makes sense for the sugar amount to increase by the same amount each time.
Activity Synthesis
Display the table for all to see and ask students to share the answers they calculated for each missing entry. After the table is complete, ask the students if they agree or disagree with the values in the table. Select students to share who used the scale factor or constant of proportionality methods to find the equivalent ratios to share their reasoning. Record their ideas directly on the table if possible and display for all to see.
3.2: The Price of Rope (15 minutes)
Activity
The purpose of this activity is to ensure students understand how an abbreviated table can be used to solve a problem (the most abbreviated table consists of only two rows). Students may have done some work like this in grade 6, in which case this activity serves to reinforce and remind. For teachers accustomed to procedures for “setting up a proportion,” this approach is very similar, except that students have the column headings to help make sure they get the numbers in the right places. Also, they should get a better idea for why they are multiplying and dividing, because they are finding and using either a scale factor or the constant of proportionality. (Note that using the constant of proportionality is easier, and also the natural way you would think about calculating the price of any amount of something.)
Launch
Students should be comfortable with Kiran's method from their work with tables of equivalent ratios in grade 6. However, if needed, show them this even longer solution method first and let them examine it. Ask why Lin decided to multiply by \(\frac13\). Once students are comfortable with the reasoning shown, explain that you will be looking at more efficient ways of solving this problem with a table.
Lin’s method:

Arrange students in groups of 2. Give students 2–3 minutes of quiet work time and then time to discuss their solutions with their partner. Follow with a whole-class discussion around the method they think Priya used.
Design Principle(s): Optimize output (for explanation); Support sense-making
Student Facing
Two students are solving the same problem: At a hardware store, they can cut a length of rope off of a big roll, so you can buy any length you like. The cost for 6 feet of rope is $7.50. How much would you pay for 50 feet of rope, at this rate?
-
Kiran knows he can solve the problem this way.
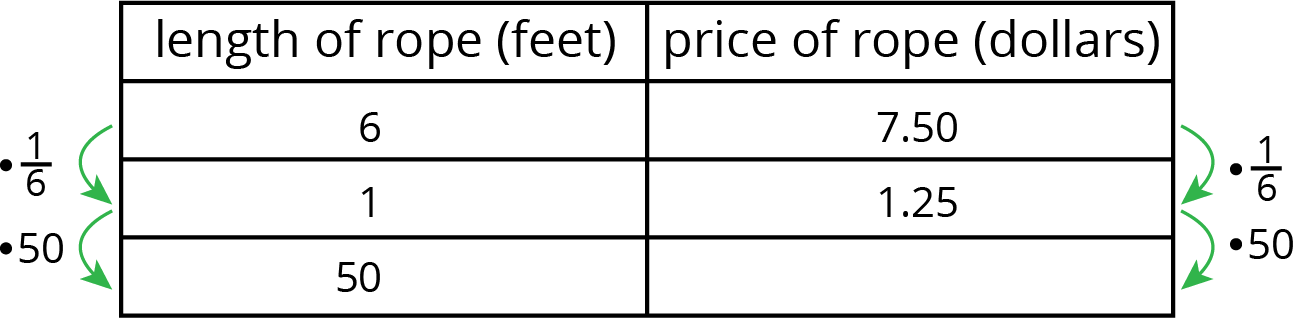
What would be Kiran's answer?
-
Kiran wants to know if there is a more efficient way of solving the problem. Priya says she can solve the problem with only 2 rows in the table.
length of rope (feet) price of rope (dollars) 6 7.50 50 What do you think Priya's method is?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may struggle to progress with Priya's method because the arrows are not drawn in the image and none of the values given are easily divisible. There are many supporting questions that could be asked.
- What if we knew the price of 1 foot of rope?
- If 6 times something is 7.5, how can we find the something?
Activity Synthesis
Ask selected students to show the way they solved the problem. If no students come up with one of these methods, display it for all to see.
Scale factor method:
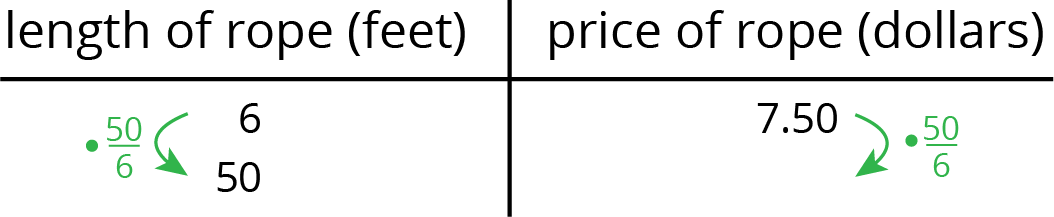
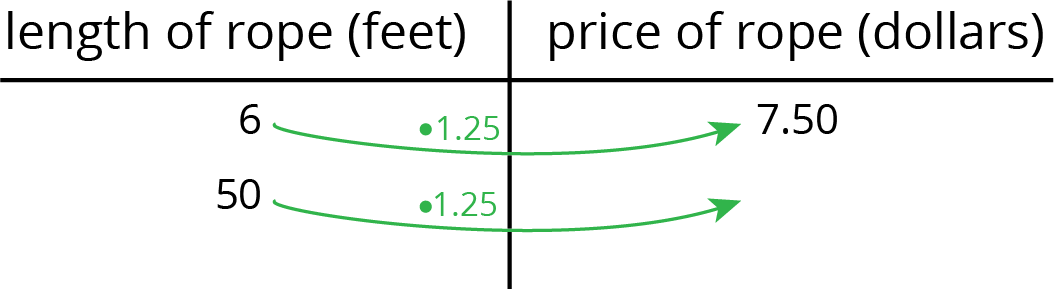
Constant of proportionality method:
Ask students:
- “How did you find the scale factor?”
- “How did you find the constant of proportionality?”
- “What does the constant of proportionality (1.25) mean in this context?”
- “Which method is your preference to use? Why?”
Although either method will work, there are reasons to prefer using the constant of proportionality to approach problems like these. First, the constant of proportionality 1.25 means something important in the problem—it’s the price of 1 foot of rope. Because of that, the 1.25 could be easily used to compute the price of any length of rope. If no students bring it up, point out that the equation \(y=1.25x\) could be used to relate any length of rope, \(x\), to its price, \(y\).
3.3: Swimming, Manufacturing, and Painting (10 minutes)
Activity
In this activity students use proportional relationships to solve problems. Although students might remember a few of the problems from previous lessons, students are asked to answer different questions. Students first need to recognize that the situation involves a proportional relationship and then use that knowledge to solve the problems. Notice that the problems decrease in the amount of scaffolding in order to build confidence for students as they work through them. Look out for students who have a systematic way of approaching these problems, and ask them to share their strategy during the discussion.
Launch
Give students 3–5 minutes of quiet work time, followed by whole-class discussion.
Supports accessibility for: Organization; Attention
Student Facing
-
Tyler swims at a constant speed, 5 meters every 4 seconds. How long does it take him to swim 114 meters?
distance (meters) time (seconds) 5 4 114 -
A factory produces 3 bottles of sparkling water for every 8 bottles of plain water. How many bottles of sparkling water does the company produce when it produces 600 bottles of plain water?
number of bottles
of sparkling waternumber of bottles
of plain water -
A certain shade of light blue paint is made by mixing \(1\frac12\) quarts of blue paint with 5 quarts of white paint. How much white paint would you need to mix with 4 quarts of blue paint?
-
For each of the previous three situations, write an equation to represent the proportional relationship.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Different nerve signals travel at different speeds.
- Pressure and touch signals travel about 250 feet per second.
- Dull pain signals travel about 2 feet per second.
- How long does it take you to feel an ant crawling on your foot?
- How much longer does it take to feel a dull ache in your foot?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may struggle to continue working as the scaffolding is decreased. Consider using these questions to prompt students:
- What are the two associated quantities in this problem?
- How many quarts of blue paint are needed for 1 quart of white paint?
Activity Synthesis
Students may have used the same method for each problem. For this reason, it might not be necessary to go over every problem. For the second question, you might select 2 different students who used the different methods to share their strategy. For the third question, ask students to share how they knew which quantities to put into the table. You might also ask:
- Does it matter which heading goes in which column?
- Do you get a different answer if you switch them? Why or why not?
- Would your strategy change if you switched them? Why or why not?
Ask students where they got stuck and what helped them to move through the hard parts. (Making a table; using the given information to figure out new information.)
Design Principle(s): Maximize meta-awareness
3.4: Finishing the Race and More Orange Juice (10 minutes)
Optional activity
The purpose of this activity is to give students an opportunity to solve proportional relationships with fractions without the scaffolded support as given in the previous activity (MP1). If students get stuck, here are some questions to ask:
- How many miles do they run in one hour?
- How many cups of orange juice concentrate are needed for one cup of water?
Monitor for students who are using the constant of proportionality strategy they learned in an earlier activity. These students should be asked to share during the discussion.
Launch
Give students 3–5 minutes of quiet work time followed by whole-class discussion.
If time is limited, pick one of the problems to talk about during the discussion.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Design Principle(s): Optimize output (for explanation)
Student Facing
-
Lin runs \(2\frac34\) miles in \(\frac25\) of an hour. Tyler runs \(8\frac23\) miles in \(\frac43\) of an hour. How long does it take each of them to run 10 miles at that rate?
-
Priya mixes \(2\frac12\) cups of water with \(\frac13\) cup of orange juice concentrate. Diego mixes \(1\frac23\) cups of water with \(\frac14\) cup orange juice concentrate. How much concentrate should each of them mix with 100 cups of water to make juice that tastes the same as their original recipe? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is for students to share how they solved proportion problems involving fractions. Select previously identified students to share their method for finding a solution. Ask students to describe why they chose to calculate the constant of proportionality for this problem and how that helped them with finding the solution.
Lesson Synthesis
Lesson Synthesis
In this lesson, we worked efficiently with tables.
“How can we use a table that only has two rows to solve a problem about a proportional relationship?” (Calculate either a scale factor or the constant of proportionality, use this as a multiplier.)
3.5: Cool-down - Walnuts in Bulk (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
If we identify two quantities in a problem and one is proportional to the other, then we can calculate the constant of proportionality and use it to answer other questions about the situation. For example, Andre runs at a constant speed, 5 meters every 2 seconds. How long does it take him to run 91 meters at this rate?
In this problem there are two quantities, time (in seconds) and distance (in meters). Since Andre is running at a constant speed, time is proportional to distance. We can make a table with distance and time as column headers and fill in the given information.
| distance (meters) | time (seconds) |
|---|---|
| 5 | 2 |
| 91 |
To find the value in the right column, we multiply the value in the left column by \(\frac25\) because \(\frac25 \boldcdot 5 = 2\). This means that it takes Andre \(\frac25\) seconds to run one meter.
At this rate, it would take Andre \(\frac25 \boldcdot 91 = \frac{182}{5}\), or 36.4 seconds to walk 91 meters. In general, if \(t\) is the time it takes to walk \(d\) meters at that pace, then \(t = \frac25 d\).