Lesson 5
Say It with Decimals
5.1: Notice and Wonder: Fractions to Decimals (5 minutes)
Warm-up
The purpose of this warm-up is to get students ready to think about decimal expansions of fractions. This will be useful in the next activity when students use long division to find decimal expansions of different fractions and find out why some repeat and others don't. In this activity, they are given calculator answers for different unit fractions (don't have to be unit fractions, could be any fractions) and they are starting to notice and verbalize different patterns. By the end of this activity they should be curious about why the decimal expansions of different fractions behave so differently.
Launch
Arrange students in groups of 2. Tell students that they will look at a collection of decimals, and their job is to think of at least one thing they notice and at least one thing they wonder. Display the image for all to see. Ask students to give a signal when they have noticed or wondered about something. Give students 1 minute of quiet think time, and then 1 minute to discuss the things they notice with their partner, followed by a whole-class discussion.
Student Facing
A calculator gives the following decimal representations for some unit fractions:
\(\frac12 = 0.5\)
\(\frac13 =0.3333333\)
\(\frac14 = 0.25\)
\(\frac15 = 0.2\)
\(\frac16 = 0.1666667\)
\(\frac17 = 0.142857143\)
\(\frac18 = 0.125\)
\(\frac19 = 0.1111111\)
\(\frac{1}{10} = 0.1 \)
\( \frac{1}{11}=0.0909091\)
What do you notice? What do you wonder?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share the things they noticed and wondered. Record and display their responses for all to see. If possible, record the relevant reasoning on or near the image. After each response, ask the class if they agree or disagree and to explain alternative ways of thinking, referring back to the images each time. If rounding does not come up during the conversation, ask students to discuss this idea.
5.2: Repeating Decimals (15 minutes)
Activity
This activity introduces students to the term repeating for describing the decimal they get after using long division to convert a fraction. If desired, the term terminating can also be introduced.
Launch
Explain to students that we can use long division to calculate the decimal representation of a fraction. For example, \(\frac78\) is equal to \(7 \div 8\).
\(\displaystyle \require{enclose} \begin{array}{rll} 0.875 \\[-3pt] 8 \enclose{longdiv}{7\phantom{.000}} \\[-3pt] \underline{-0}\phantom{..00} \\[-3pt] 70\phantom{.00} \\[-3pt] \underline{-64}\phantom{.00} \\[-3pt] 60\phantom{.0} \\[-3pt] \underline{-56}\phantom{.0} \\[-3pt] 40\phantom{.}\\[-3pt] \underline{-40}\phantom{.}\\[-3pt] 0\phantom{.} \end{array} \)
Using long division, we see that \(\frac78\) is equal to 0.875. This process works for any fraction.
Here is another example: \(\frac{7}{12}\) is equal to \(7 \div 12\).
\(\displaystyle \require{enclose} \begin{array}{rll}0.58333 \\[-3pt] 12 \enclose{longdiv}{7\phantom{.00000}} \\[-3pt] \underline{-0}\phantom{..0000} \\[-3pt] 70\phantom{.0000} \\[-3pt] \underline{-60}\phantom{.0000} \\[-3pt] 100\phantom{.000} \\[-3pt] \underline{-96}\phantom{.000} \\[-3pt] 40\phantom{.00}\\[-3pt] \underline{-36}\phantom{.00}\\[-3pt] 40\phantom{.0}\\[-3pt] \underline{-36}\phantom{.0}\\[-3pt] 40\phantom{.} \\[-3pt] \underline{-36}\phantom{.}\\[-3pt] 4\phantom{.}\end{array} \)
In this case, the division will never result in a remainder of 0. Because we keep getting 3 over and over again, this is called a repeating decimal and can be written as \(0.58\overline{3}\).
Arrange students in groups of 2. Give students 3–5 minutes of quiet think time on the first problem and 1–2 minutes to compare their responses and discuss the second question with their partner. Then give students 2–3 minutes of quiet think time on the remaining question. Follow with whole-class discussion.
Student Facing
-
Use long division to express each fraction as a decimal.
\(\frac{9}{25}\)
\(\frac{11}{30}\)
\(\frac{4}{11}\)
- What is similar about your answers to the previous question? What is different?
- Use the decimal representations to decide which of these fractions has the greatest value. Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
One common approximation for \(\pi\) is \(\frac{22}{7}\). Express this fraction as a decimal. How does this approximation compare to 3.14?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may set up their long division with the divisor and dividend in the wrong places. They will get \(2.\overline7\), \(2.\overline{72}\), and 2.75 as their answers. Prompt them to think about what is being divided and what it is being divided by.
Activity Synthesis
The purpose of this discussion is to help students make sense of the value of repeating decimals. Ask students to explain the strategies they used to answer question 3. If no students mention place value, ask them to use this language to describe their strategies.
Design Principle(s): Support sense-making; Optimize output for (comparison)
5.3: More and Less with Decimals (15 minutes)
Activity
This activity continues work done in the previous lesson that connected various representations of proportional relationships including images, equations, and descriptions. In this activity students match diagrams, descriptions, and equations that represent a proportional relationship, involving variables \(x\) and \(y\). Students then create their own diagram to represent an equation.
Identify students that create diagrams representing each of the unmatched equations, so they can share their work during the discussion.
Launch
Give students 7–10 minutes of quiet think time on the questions. Follow with whole-class discussion.
Supports accessibility for: Conceptual processing; Memory
Student Facing
-
Match each diagram with a description and an equation.
Diagrams:
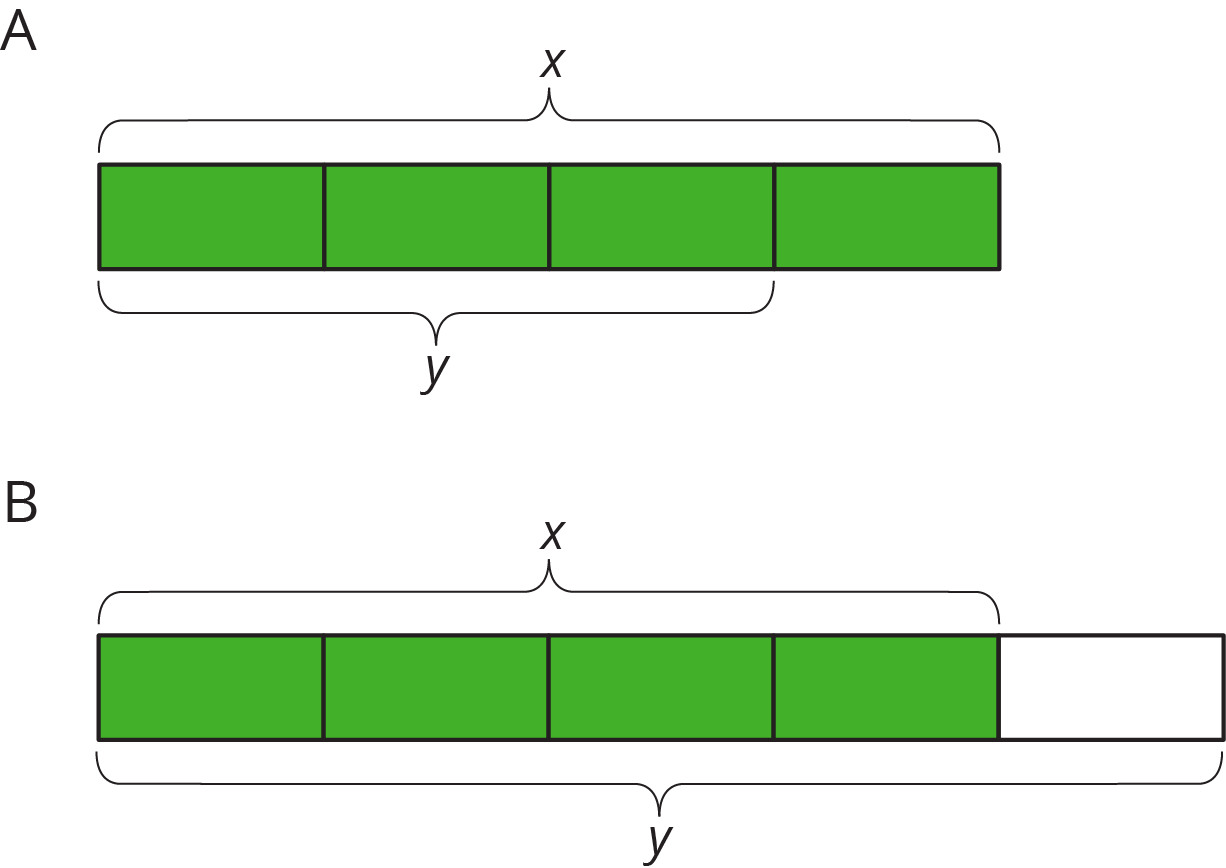
Descriptions:
An increase by \(\frac14\)
An increase by \(\frac13\)
An increase by \(\frac23\)
A decrease by \(\frac15\)
A decrease by \(\frac14\)
Equations:
\(y=1.\overline{6}x\)
\(y=1.\overline{3}x\)
\(y=0.75x\)
\(y=0.4x\)
\(y=1.25x\)
- Draw a diagram for one of the unmatched equations.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask previously identified students to share their diagrams and explain how they represent the equation they chose. Then, ask students that did not share their diagrams to explain whether \(x\) (or \(y\)) is increased or decreased by some amount in the discussed equations.
Design Principle(s): Maximize meta-awareness
5.4: Card Sort: More Representations (10 minutes)
Optional activity
This activity continues the card sort from the previous lesson by including a fourth representation for each relationship, an equation with a decimal instead of a fraction.
Launch
Remind students of card sort activity of the earlier lesson. Demonstrate how to set up and do the matching activity. Choose a student to be your partner. Mix up the rest of the cards and place them face-up. Point out that each card contains a description, table, or equation (with fractions or decimals). Select one of each style of card and then explain to your partner why you think the cards do or do not match. Demonstrate productive ways to agree or disagree (e.g., by explaining your mathematical thinking, asking clarifying questions, etc.).
Arrange students in groups of 2. Give each group pre-printed cut-up slips for matching. Place two copies of uncut blackline masters in envelopes to serve as answer keys.
Supports accessibility for: Conceptual processing; Organization
Design Principle(s): Support sense-making; Optimize output (for justification)
Student Facing
Your teacher will give you a set of cards that have proportional relationships represented 2 different ways: as descriptions and equations. Mix up the cards and place them all face-up.
Take turns with a partner to match a description with an equation.
- For each match you find, explain to your partner how you know it’s a match.
- For each match your partner finds, listen carefully to their explanation, and if you disagree, explain your thinking.
- When you have agreed on all of the matches, check your answers with the answer key. If there are any errors, discuss why and revise your matches.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
After students complete the task, ask students to share a few of their arguments for the matches they came up with (not all need to be shared). Ask students to compare the equations with decimals and fractions.
Lesson Synthesis
Lesson Synthesis
This lesson was similar to the last one, except we focused on writing things with decimals.
“Give examples of how we can use the distributive property to create equivalent expressions that make it easier for us to calculate an amount plus (or minus) a fraction of that amount, but written with decimals” (e.g. \(100x+12x=112x\))
5.5: Cool-down - Reading More (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Long division gives us a way of finding decimal representations for fractions.
For example, to find a decimal representation for \(\frac{9}{8}\), we can divide 9 by 8.
\(\require{enclose} \begin{array}{r} 1.125 \\[-3pt] 8 \enclose{longdiv}{9.000}\kern-.2ex \\[-3pt] \underline{8{\phantom{.0}}} \phantom{00} \\[-3pt] 1\phantom{.}0\phantom{00} \\[-3pt] \underline{8\phantom{0}}\phantom{0} \\[-3pt] 20\phantom{0} \\[-3pt] \underline{16\phantom{0}} \\[-3pt] \phantom{0} 40 \\[-3pt] \underline{40} \\[-3pt] 0 \\ \end{array}\)
So \(\frac{9}{8} = 1.125\).
Sometimes it is easier to work with the decimal representation of a number, and sometimes it is easier to work with its fraction representation. It is important to be able to work with both. For example, consider the following pair of problems:
- Priya earned \(x\) dollars doing chores, and Kiran earned \(\frac{6}{5}\) as much as Priya. How much did Kiran earn?
- Priya earned \(x\) dollars doing chores, and Kiran earned 1.2 times as much as Priya. How much did Kiran earn?
Since \(\frac{6}{5}=1.2\), these are both exactly the same problem, and the answer is \(\frac{6}{5}x\) or \(1.2x\). When we work with percentages in later lessons, the decimal representation will come in especially handy.