Lesson 12
Finding the Percentage
12.1: Tax, Tip, and Discount (5 minutes)
Warm-up
In this warm-up, students are reminded of the tape diagram method for understanding parts of a whole. The tape diagrams are used in the context of tips, taxes, and discounts.
Launch
Students in groups of 2. Allow students 2 minutes quiet work time followed by partner then whole-class discussion.
Student Facing
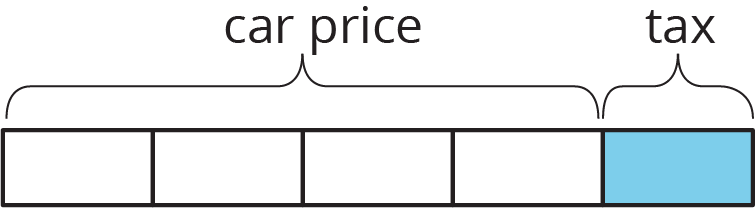
What percentage of the car price is the tax?
What percentage of the food cost is the tip?

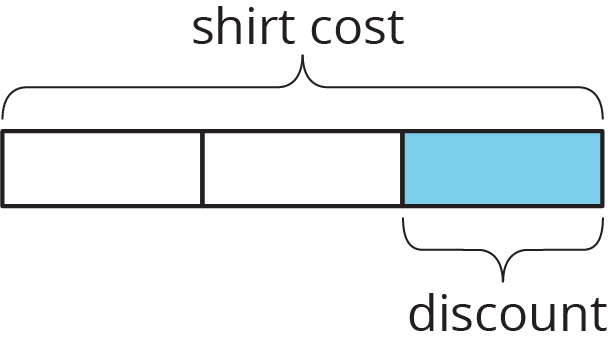
What percentage of the shirt cost is the discount?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of the discussion is for students to recognize that a tape diagram can be useful for working with percentages as part of a whole.
Consider asking these discussion questions:
- "The tax on the car is what fraction of the car price before tax was added on?" (One fourth)
- "With the tip added on, how is the length of the entire bar related to the length of the bar that just represents the food cost?" (It is 1.2 times as long.)
- "How does the value \(\frac{2}{3}\) relate to the last tape diagram?" (It represents the fraction of the original cost of the shirt that is the price of the shirt after the discount.)
12.2: What Is the Percentage? (10 minutes)
Activity
In this activity, students continue to practice finding percentages from dollar amounts including commission, tip, and markdown. Some of the questions require multiple steps to solve for the percentage needed.
As students work, monitor for students who take different approaches to solving the multiple steps involved in these problems. For example, some students may subtract the discounted price from the original price to find the amount that the item has been marked down before finding the percentage of markdown. Other students may find the percentage of the original price used for the discounted price and then subtract that from 100%.
Launch
Arrange students in groups of 2. Give students 3–5 minutes of quiet work time followed by partner and whole-class discussions.
Student Facing
-
A salesperson sold a car for $18,250 and their commission is $693.50. What percentage of the sale price is their commission?
-
The bill for a meal was $33.75. The customer left $40.00. What percentage of the bill was the tip?
-
The original price of a bicycle was $375. Now it is on sale for $295. What percentage of the original price was the markdown?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
To make a Koch snowflake,
- Start with an equilateral triangle. This is step 1.
- Divide each side into 3 equal pieces. Construct a smaller equilateral triangle on the middle third. This is step 2.
- Do the same to each of the newly created sides. This is step 3.
- Keep repeating this process.

By what percentage does the perimeter increase at step 2? Step 3? Step 10?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of the discussion is for students to share methods for finding percentages in problems that require multiple steps.
Select the previously identified students to share their different methods for solving the last 2 questions. Sequence so strategies using diagrams come first, and those using equations come second.
Supports accessibility for: Language; Social-emotional skills
Design Principle(s): Support sense-making
12.3: Info Gap: Sporting Goods (20 minutes)
Activity
The purpose of this info gap activity is for students to identify the essential information needed to determine the total savings after various discounts are applied to different items.
The info gap structure requires students to make sense of problems by determining what information is necessary, and then to ask for information they need to solve it. This may take several rounds of discussion if their first requests do not yield the information they need (MP1). It also allows them to refine the language they use and ask increasingly more precise questions until they get the information they need (MP6).
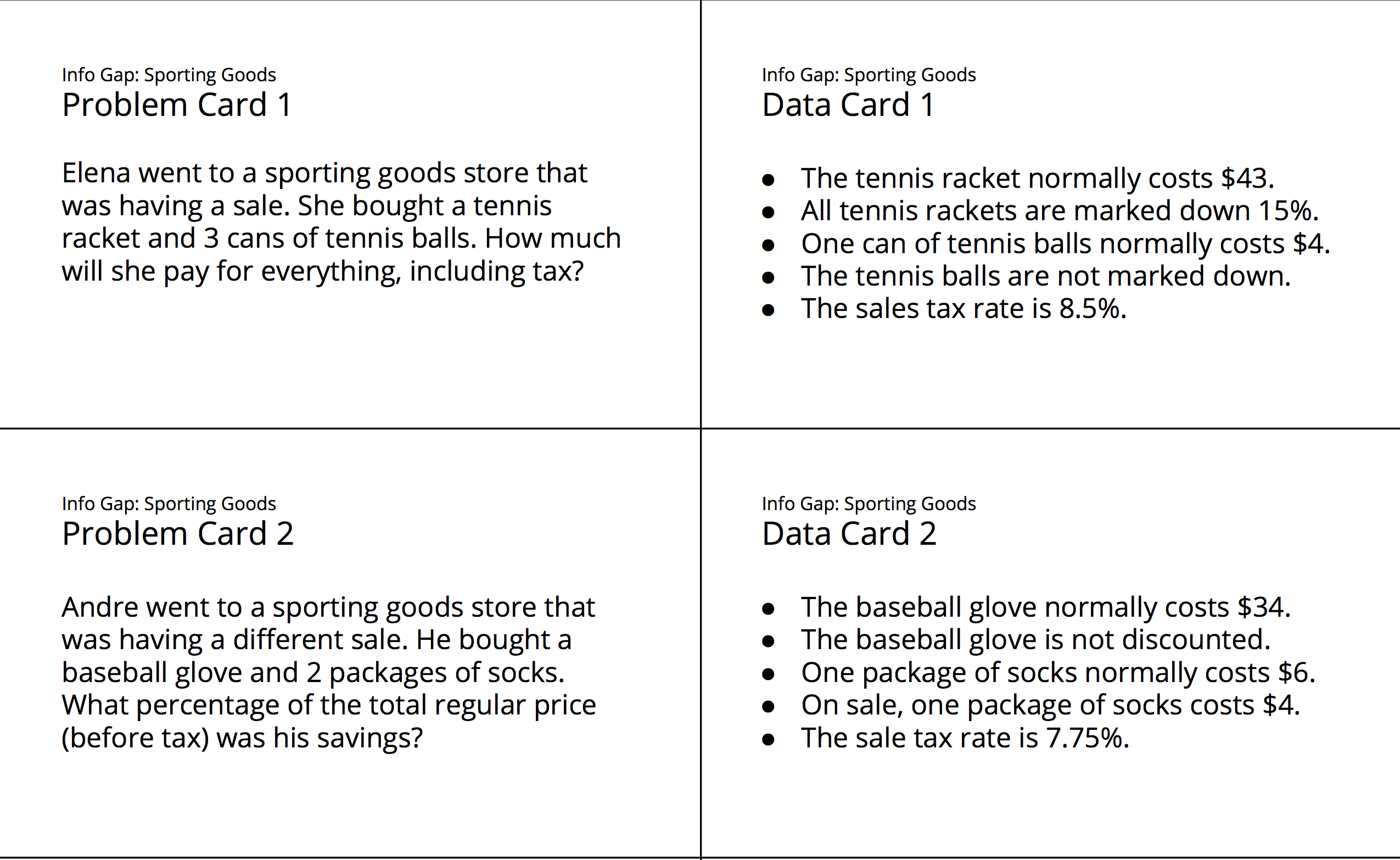
Here is the text of the cards for reference and planning:
Launch
Provide access to calculators. Tell students they will continue to work with percentages and their similarities to proportional relationships. Explain the Info Gap structure and consider demonstrating the protocol if students are unfamiliar with it. There are step-by-step instructions in the student task statement.
Arrange students in groups of 2. In each group, distribute a problem card to one student and a data card to the other student. After you review their work on the first problem, give them the cards for a second problem and instruct them to switch roles.
Supports accessibility for: Memory; Organization
Design Principle(s): Cultivate Conversation
Student Facing
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
-
Silently read your card and think about what information you need to be able to answer the question.
-
Ask your partner for the specific information that you need.
-
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
-
Share the problem card and solve the problem independently.
-
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
-
Silently read your card.
-
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
-
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
-
Read the problem card and solve the problem independently.
-
Share the data card and discuss your reasoning.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might fail to notice that Elena and Andre buy multiple cans of tennis balls and packages of socks, respectively. Ask students to figure out how much 2 packages of socks (or 3 cans of tennis balls) will cost.
If students automatically give the 15% discount on all of Elena's purchases, ask students which of Elena's items fall under the discount.
Students might apply the discount after the adding in the sales tax. Remind students that the discount gets applied to the subtotal before the tax is calculated.
Some students may include the sales tax when calculating the percentage of Andre's savings. Remind them that the problem specifies "before tax."
Activity Synthesis
The purpose of the discussion is for students to recognize what information may be needed to solve problems involving percentages for prices of items.
After students have completed their work, share the correct answers and ask students to discuss the different ways they solved this problem. Some guiding questions:
- "What information did you and your partner have to figure out?"
- "How did you determine the cost of Elena's tennis racket?" (Multiply the original cost by 0.85 or multiply by 0.15 and subtract from the original cost.)
- "How did you determine the total cost after tax for Elena's purchases?" (Multiply the total by 1.085 or multiply by 0.085 and add to the original cost.)
- "What different calculations did you have to make for Andre and Elena’s situations?"
- "Was there information given that you did not need to use?"
Lesson Synthesis
Lesson Synthesis
In this lesson, students found the percentage increase or decrease given the original and final amounts.
- “When the original price and discounted prices are known, how can we find the percent markdown?” (Find the difference and then find the percentage that difference is of the original price.)
- “When you know the original price of an item and the price you paid at a register, how can you find the tax rate?” (Find the difference and then find the percentage that difference is of the original price.)
12.4: Cool-down - Shoes on Sale (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
To find a 30% increase over 50, we can find 130% of 50.
\(1.3 \boldcdot 50 = 65\)
To find a 30% decrease from 50, we can find 70% of 50.
\(0.7 \boldcdot 50 = 35\)
If we know the initial amount and the final amount, we can also find the percent increase or percent decrease. For example, a plant was 12 inches tall and grew to be 15 inches tall. What percent increase is this? Here are two ways to solve this problem:
The plant grew 3 inches, because \(15 - 12=3\). We can divide this growth by the original height, \(3 \div 12 = 0.25\). So the height of the plant increased by 25%.
The plant's new height is 125% of the original height, because \(15 \div 12=1.25\). This means the height increased by 25%, because \(125 - 100 = 25\).
Here are two ways to solve the problem: A rope was 2.4 meters long. Someone cut it down to 1.9 meters. What percent decrease is this?
The rope is now \(2.4 - 1.9\), or 0.5 meters shorter. We can divide this decrease by the original length, \(0.5 \div 2.4 = 0.208\overline3\). So the length of the rope decreased by approximately 20.8%.
The rope's new length is about 79.2% of the original length, because \(1.9 \div 2.4 = 0.791\overline6\). The length decreased by approximately 20.8%, because \(100 - 79.2 = 20.8\).