Lesson 7
Exploring the Area of a Circle
7.1: Estimating Areas (5 minutes)
Warm-up
The purpose of this warm-up is for students to estimate the area of a circle using what they know about the area of polygons. The first picture with no grid prompts students to visualize decomposing and rearranging pieces of the figures in order to compare their areas. Using the grid, students are able to estimate the areas and discuss their strategies.
Launch
Arrange students in groups of 3. Display the first image with no grid for all to see.
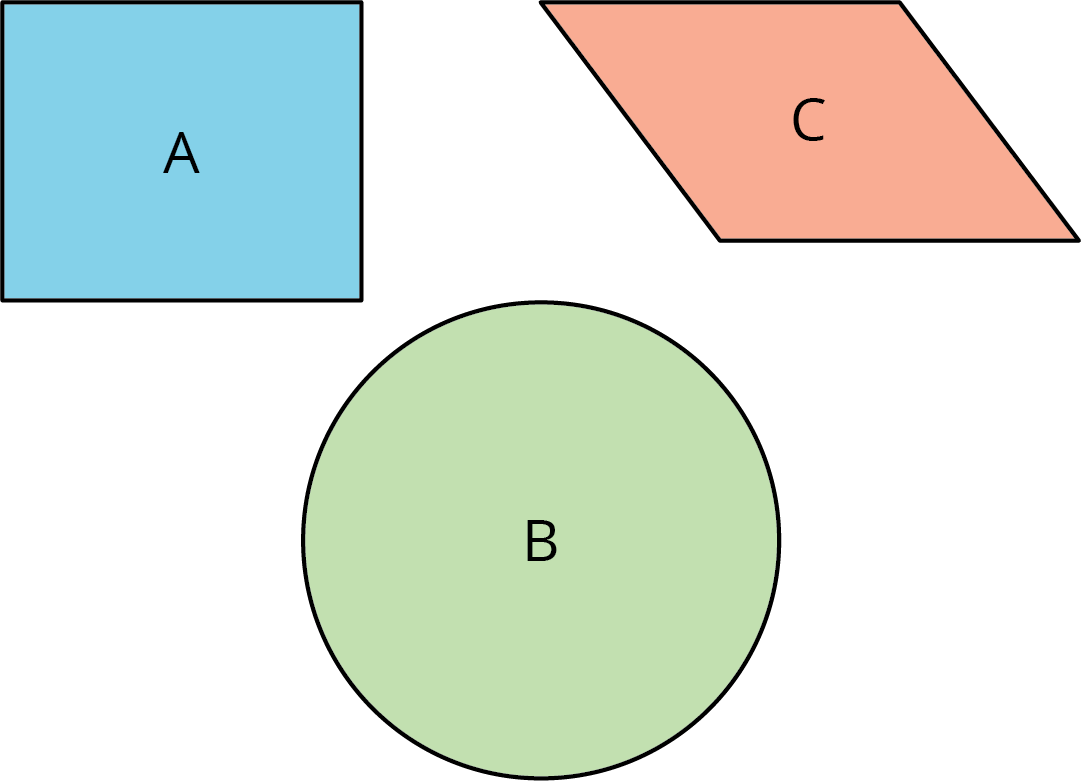
Ask students to give a signal when they have an idea which figure has the largest area. Give students 30 seconds of quiet think time followed by 1 minute to discuss their reasoning with a partner. Next display the image on a grid.
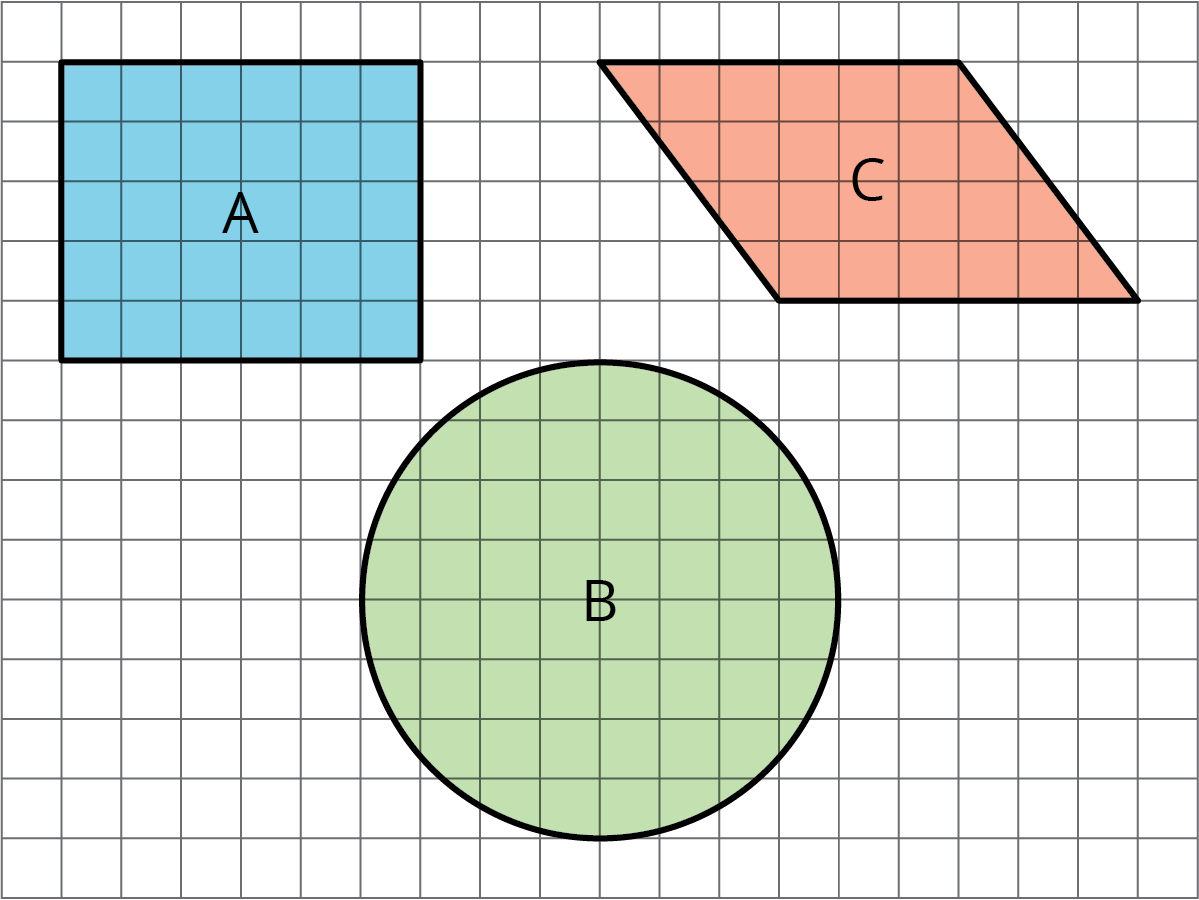
Ask students to discuss with their group how they would find or estimate the area of each of the figures. Tell them to share their ideas with their group.
Student Facing
Your teacher will show you some figures. Decide which figure has the largest area. Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite selected students to share their strategies and any information in the image that would inform their responses. After each explanation, solicit questions from the class that could help the student clarify his or her reasoning. Ask the whole class to discuss their strategies for finding or estimating the area. Ask them if they think it is possible to calculate the area of the circle exactly. Tell them that trying to find the area of a circle will be the main topic for this lesson.
Refer to MLR 7 (Compare and Connect). Prompt students with questions like: What information was useful for solving the problem? What formulas or prior knowledge did you use to approach the problem? What did you do that was similar to another student? How did you estimate when there was not a complete grid block?
7.2: Estimating Areas of Circles (20 minutes)
Activity
In a previous lesson, students measured various circular objects and graphed the measurements to see that there appears to be a proportional relationship between the diameter and circumference of a circle. In this activity, students use a similar process to see that the relationship between the diameter and area of a circle is not proportional. This echoes the earlier exploration comparing the length of a diagonal of a square to the area of the square, which was also not proportional.
Each group estimates the area of one smaller circle and one larger circle. After estimating the area of their circles, students graph the class’s data on a coordinate plane to notice that the data points curve upward instead of making a straight line through the origin. Watch for students who use different methods for estimating the area of the circles (counting full and partial grid squares inside the circle, surrounding the circle with a square and removing full and partial grid squares) and invite them to share in the discussion.

Launch
Arrange students in groups of 2.
For classes using the print version, distribute the grids with the circles already drawn—one set of circles to each group of students from the Estimating Areas of Circles blackline master.
For classes using the digital version of the activity, assign each group of students a pair of diameters from this set:
- 2 cm and 16 cm
- 5 cm and 10 cm
- 3 cm and 12 cm
- 6 cm and 18 cm
- 4 cm and 20 cm
- 7 cm and 14 cm
Encourage students to look for strategies that will help them efficiently count the area of their assigned circles. Give students 4–5 minutes of group work time.
After students have finished estimating the areas of their circles, display the blank coordinate grid from the activity statement and have students plots points for their measurements. Give students 3–4 minutes of quiet work time, followed by whole-class discussion.
Student Facing
Your teacher will give your group two circles of different sizes.
- Set the diameter of your assigned circle and use the applet to help estimate the area of the circle.
Note: to create a polygon, select the Polygon tool, and click on each vertex. End by clicking the first vertex again. For example, to draw triangle \(ABC\), click on \(A\)-\(B\)-\(C\)-\(A\).
- Record the diameter in column \(D\) and the corresponding area in column \(A\) for your circles and others from your classmates.
-
In a previous lesson, you graphed the relationship between the diameter and circumference of a circle. How is this graph the same? How is it different?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2.
For classes using the print version, distribute the grids with the circles already drawn—one set of circles to each group of students from the Estimating Areas of Circles blackline master.
For classes using the digital version of the activity, assign each group of students a pair of diameters from this set:
- 2 cm and 16 cm
- 5 cm and 10 cm
- 3 cm and 12 cm
- 6 cm and 18 cm
- 4 cm and 20 cm
- 7 cm and 14 cm
Encourage students to look for strategies that will help them efficiently count the area of their assigned circles. Give students 4–5 minutes of group work time.
After students have finished estimating the areas of their circles, display the blank coordinate grid from the activity statement and have students plots points for their measurements. Give students 3–4 minutes of quiet work time, followed by whole-class discussion.
Student Facing
Your teacher will give your group two circles of different sizes.
-
For each circle, use the squares on the graph paper to measure the diameter and estimate the area of the circle. Record your measurements in the table.
diameter (cm) estimated area (cm2) -
Plot the values from the table on the class coordinate plane. Then plot the class’s data points on your coordinate plane.

-
In a previous lesson, you graphed the relationship between the diameter and circumference of a circle. How is this graph the same? How is it different?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
How many circles of radius 1 unit can you fit inside each of the following so that they do not overlap?
- a circle of radius 2 units?
- a circle of radius 3 units?
- a circle of radius 4 units?
If you get stuck, consider using coins or other circular objects.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students might be unsure on how to count the squares around the border of the circle that are only partially included. Let them come up with their own idea, but if they need additional support, suggest that they round up to a whole square when it looks like half or more of the square is within the circle and round down to no square when it looks like less than half the square is within the circle.
Activity Synthesis
Invite selected students to share their strategies for estimating the area of their circle.
Next, ask "Is the relationship between the diameter and the area of a circle a proportional relationship?" (No.) Invite students to explain their reasoning. (The points do not lie on a straight line through \((0, 0)\).)
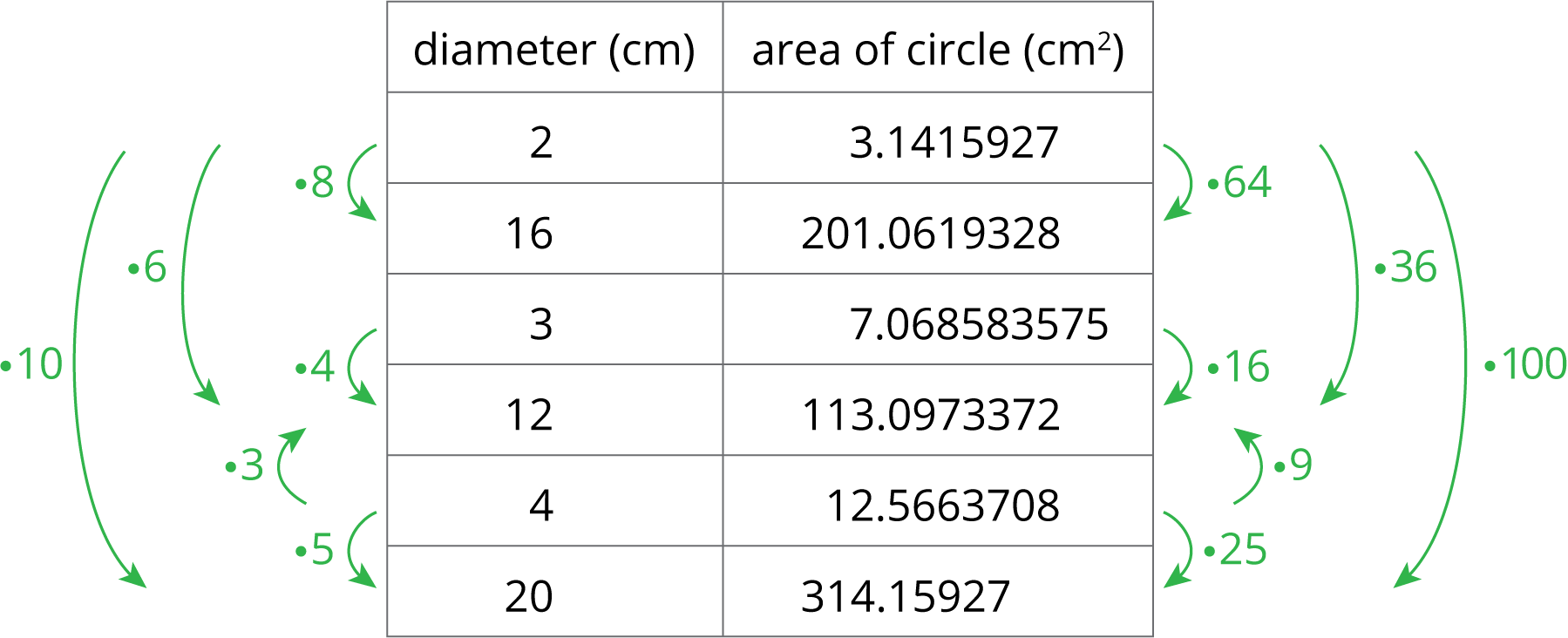
To help students see and express that the relationship is not proportional, consider adding a column to the table of measurements to record the quotient of the area divided by the diameter. Here is a table of sample values.
| diameter (\(\text{cm}\)) | estimated area (\(\text{cm}^2\)) | \(\text{area} \div \text{diameter}\) |
|---|---|---|
| 2 | 3 | 1.5 |
| 3 | 7 | 2.3 |
| 4 | 12 | 3.0 |
| 5 | 19 | 3.8 |
| 6 | 27 | 4.5 |
| 7 | 38 | 5.4 |
| 10 | 78 | 7.8 |
| 12 | 108 | 9.0 |
| 14 | 147 | 10.5 |
| 16 | 200 | 12.5 |
| 18 | 250 | 13.9 |
| 20 | 312 | 15.6 |
Remind students that there is a proportional relationship between diameter and circumference, even though there is not between diameter and area. Recall that students saw the same phenomenon when they examined the relationship between the diagonal of a square and its perimeter (proportional) and the diagonal of a square and its area (not proportional).
7.3: Covering a Circle (20 minutes)
Optional activity
In this activity students compare the area of a circle of radius \(r\) with the area of a square of side length \(r\) through trying to cover the circle with different amounts of squares. The task is open-ended so the students can look for a very rough estimate or can look for a more precise estimate. In either case, they find that the circle has area greater than 2 times the square, less than 4 times the square, and that 3 times the square looks like a good estimate.
In the discussion, students will generalize their estimates for different values of \(r\). An optional video shows how to cut up 3 squares and place them inside a circle. Since there is a little white space still showing around the cut pieces, that means that the area of a circle with radius \(r\) is close to, but a little bit more than, \(3r^2\).
Watch for how students use the square and circle provided in the problem (MP5).
Launch
Keep students in the same groups. Provide access to geometry toolkits.
Supports accessibility for: Visual-spatial processing; Conceptual processing; Organization
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
Here is a square whose side length is the same as the radius of the circle.
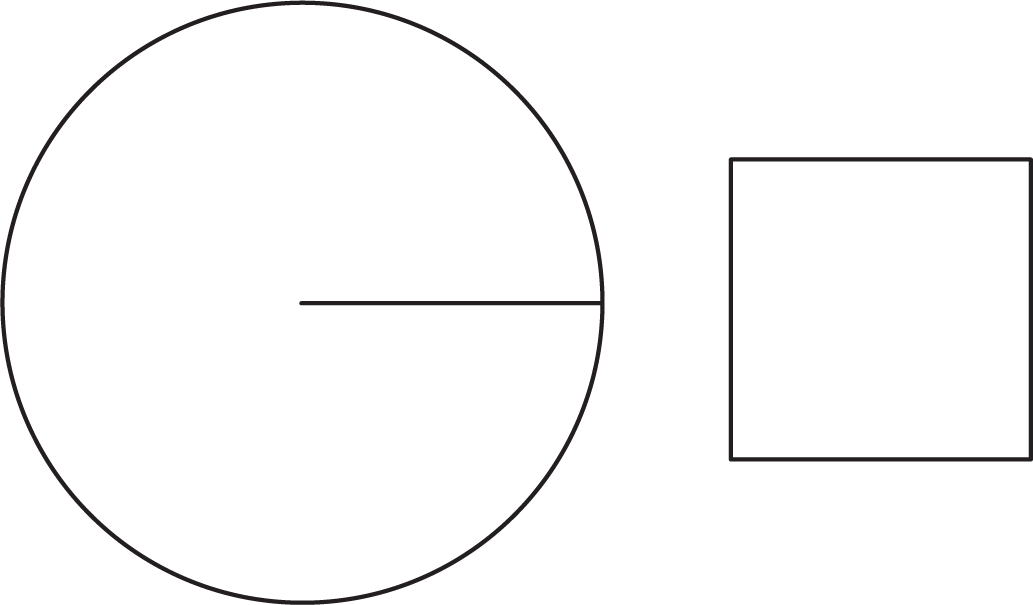
How many of these squares do you think it would take to cover the circle exactly?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may focus solely on the radius of the circle and side length of the square, not relating their work to area. As these students work, ask them what they find as they try to cover the circle each time. Reinforce the idea that as they cover the circle, they are comparing the area of the circle and squares.
If students arrive at the idea that 4 squares suffice to completely cover the circle, ask them if there is any excess. Could they cover the square with \(3\frac{1}{2}\) squares, for example?
Activity Synthesis
The goal of this discussion is for students to recognize that the area of the circle with radius \(r\) is a little more than \(3r^2\), for any size circle.
Ask the class:
- “Can two squares completely cover the circle?” (No.)
- “Can four squares completely cover the circle?” (Yes.)
- “Can three squares completely cover the circle?” (It's hard to tell for sure.)
Invite students to explain their reasoning. Consider displaying this image for students to refer to during their explanations.
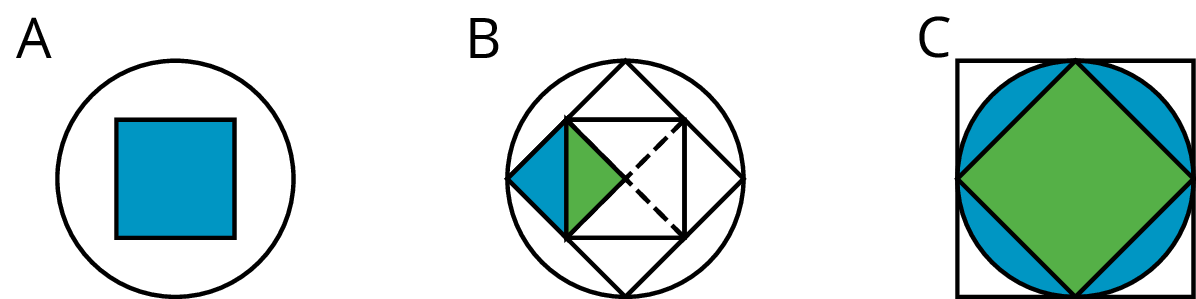
- Figure A shows that the area of the circle is larger than the area of the square, because the square can be placed inside the circle and more white space remains.
- Figure B shows that the area of the circle is larger than twice the area of the square, because the squares can be cut and repositioned to fit within the circle and some white space still remains.
- Figure C shows that the area of the circle is smaller than four times the area of the square, because the squares completely cover the circle and the corners go outside the circle.
- Figure C also shows that it is reasonable to conclude the the area of the circle is approximately equal to three times the area of the square, because it looks like the blue shaded regions (inside the circle) are close in area to the white shaded regions (outside the circle but inside the square).
Consider showing this video which makes it more apparent that three of these squares can be cut and repositioned to fit entirely within the circle.
Since there is a little white space remaining around the cut pieces, that means it would take a little bit more than three squares to cover the circle. The area of the circle is a little bit more than three times the area of one of those squares. At this point, some students may suggest that it takes exactly \(\pi\) squares to cover the circle. This will be investigated in more detail in the next lesson. If not mentioned by students, it does not need to be brought up in this discussion.
Next, guide students towards the expression \(3r^2\) by asking questions like these:
- “Does the size of the circle affect how many radius squares it takes to cover the circle?” (No, the entire picture can be scaled.)
- “If the radius of the circle were 4 units, what would be the area of the square? What would be the area of the circle?” (16 units2 and a little more than \(3 \boldcdot 16\), or 48 units2)
- “If the radius of the circle were 11 units, what would be the area of the square? What would be the area of the circle?” (121 units2 and a little more than \(3 \boldcdot 121\), or 363 units2)
- “If the circle has radius \(r\), what would be the area of the square? What would be the area of the circle?” (\(r^2\) units2 and a little more than \(3r^2\) units2)
Lesson Synthesis
Lesson Synthesis
Pose the following question: “If you have a square with side lengths equal to the radius of a circle, how many of these squares does it take to cover the circle?”
Tell students what approximation to use for this value. Have students use this approximation along with the area of such a square to calculate the area of each circle they were assigned at the beginning of class. Record their answers in a table displayed for all to see and discuss:
- “How many times larger is the diameter?”
- “Does the area increases by the same factor?”
- “Is the relationship between the diameter and area of a circle a proportional relationship? How do you know?”
Draw arrows with the scale factors to the left side of the table to illustrate the relationship between the diameters. Draw arrows on the right side of the table and label them with the factor the area is increasing by, such as “\(\boldcdot 64\)” or just write “not \(\boldcdot 8\)”.
7.4: Cool-down - Areas of Two Circles (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The circumference \(C\) of a circle is proportional to the diameter \(d\), and we can write this relationship as \(C = \pi d\). The circumference is also proportional to the radius of the circle, and the constant of proportionality is \(2 \boldcdot \pi\) because the diameter is twice as long as the radius. However, the area of a circle is not proportional to the diameter (or the radius).
The area of a circle with radius \(r\) is a little more than 3 times the area of a square with side \(r\) so the area of a circle of radius \(r\) is approximately \(3r^2\). We saw earlier that the circumference of a circle of radius \(r\) is \(2\pi r\). If we write \(C\) for the circumference of a circle, this proportional relationship can be written \(C = 2\pi r\).
The area \(A\) of a circle with radius \(r\) is approximately \(3r^2\). Unlike the circumference, the area is not proportional to the radius because \(3r^2\) cannot be written in the form \(kr\) for a number \(k\). We will investigate and refine the relationship between the area and the radius of a circle in future lessons.