Lesson 9
Applying Area of Circles
9.1: Still Irrigating the Field (5 minutes)
Warm-up
The purpose of this activity is for students to calculate a more exact answer to a problem from the previous lesson in which they estimated the area. Each answer choice listed results from using a different approximation of \(\pi\).
Launch
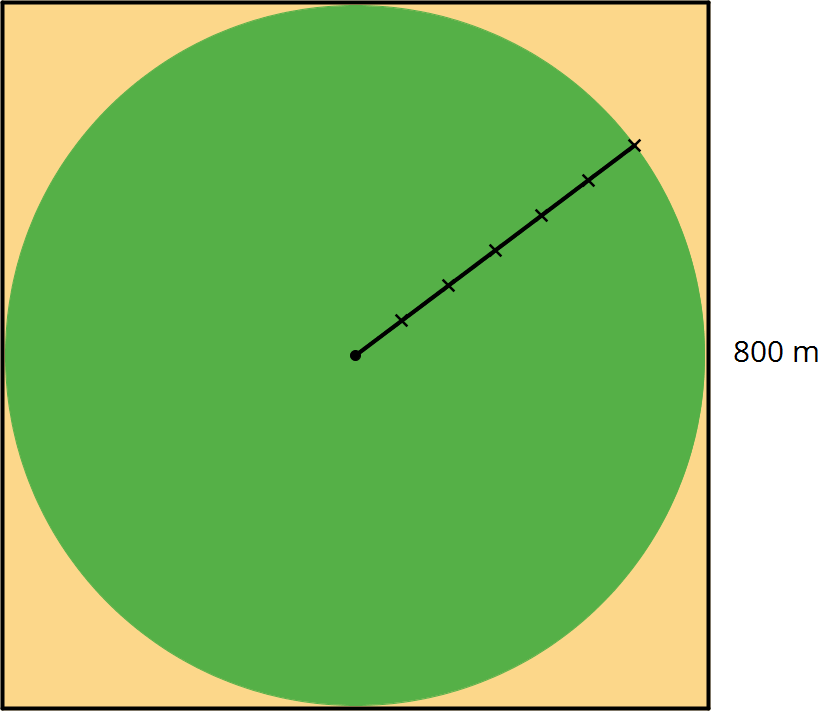
Remind students that the circular field is enclosed by a square that is 800 m on a side. If students ask what approximation they should use for \(\pi\), tell them they can choose.
Give students 2 minutes of quiet work time followed by a whole-class discussion.
Student Facing
The area of this field is about 500,000 m2. What is the field’s area to the nearest square meter? Assume that the side lengths of the square are exactly 800 m.
- 502,400 m2
- 502,640 m2
- 502,655 m2
- 502,656 m2
- 502,857 m2
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
All the answer choices are possible, but because the radius of the circle is so large, using a more approximate value for \(\pi\) can lead to a noticeable rounding error.
- \(3.14 \boldcdot 400^2 = 502,\!400\)
- \(3.1415 \boldcdot 400^2 = 502,\!640\)
- \(3.1415927 \boldcdot 400^2 \approx 502,\!655\)
- \(3.1416 \boldcdot 400^2 = 502,\!656\)
- \(\frac{22}{7} \boldcdot 400^2 \approx 502,\!857\)
The most accurate answer, \(502,\!655 \text{ m}^2\), comes from using at least 6 decimal places for \(\pi\).
9.2: Comparing Areas Made of Circles (20 minutes)
Activity
The purpose of this activity is for students to find the areas of regions involving different-sized circles and compare the strategies used. The first question introduces subtraction as a strategy to find the area around the outside of a circle. The second question introduces division to find the area of fractions of a circle.
Monitor for students who use different strategies for finding the area, including:
- Calculating 30.96 square units for Figure A, \(4 \boldcdot 7.74\) for Figure B, and \(9 \boldcdot 3.44\) for Figure C
- Realizing that all 3 figures end up being \(144 - 113.04\) so their areas had to be equal
- Noticing that Figure B is composed of 4 scaled copies of Figure A, each with a scale factor of \(\frac12\) and therefore \(\frac14\) as much area. Figure C is composed of 9 scaled copies of Figure A, each with a scale factor of \(\frac13\) and therefore \(\frac19\) as much area. (If a student does not make this realization, it is not necessary for the teacher to bring it up during the discussion.)
- Calculating 8.28 square units for Figure D and 8.71 square units for Figure E
- Realizing that Figures D has 2 fewer squares and 2 more quarter-circles (which are smaller than the squares) so it must have a smaller area
The task affords an opportunity for students to engage in MP6. Some students may leave the area expressions in terms of \(\pi\), but others may use an approximation for \(\pi\). It is very important, particularly for the first problem, that they use the same approximation for \(\pi\) in all 3 figures. Otherwise they will end up with numerically different answers.
Launch
Arrange students in groups of 2. Display the image in the first question and ask students to make a prediction before calculating. Give 30 seconds of quiet think time before sharing with their partner. Give students quiet work time followed by a whole-class discussion.
Student Facing
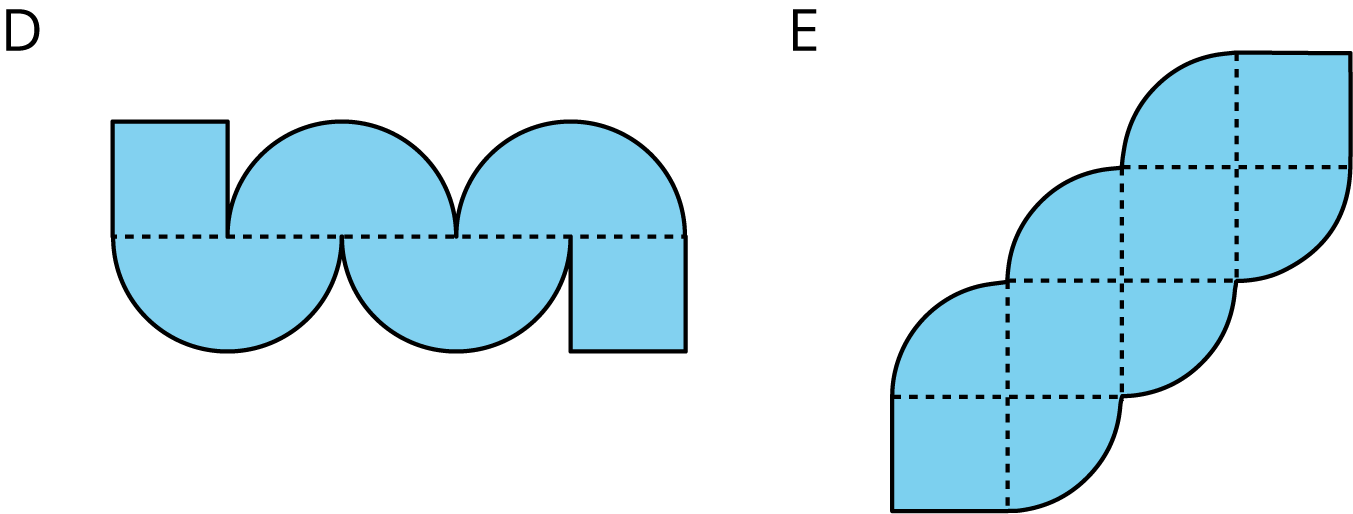
- Each square has a side length of 12 units. Compare the areas of the shaded regions in the 3 figures. Which figure has the largest shaded region? Explain or show your reasoning.

- Each square in Figures D and E has a side length of 1 unit. Compare the area of the two figures. Which figure has more area? How much more? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Which figure has a longer perimeter, Figure D or Figure E? How much longer?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
In the first question, students may not know how to find the radius of the circles. Suggest having them cut off the shaded regions and rearrange them to show that the length of each side fits half way across the circle (marking the radius).
In the second question, students might benefit from cutting and rearranging the figures. Some students might assume, based on previous activities, that the areas of both figures are equal. However, Figure D has more pieces that are parts of a circle, and Figure E has more units that are a full square. Ask students whether the fourth of the circle has the same area as the square.
Activity Synthesis
There are two main goals for this discussion: for students to notice ways to be more efficient when comparing the areas of the regions and to be introduced to expressing answers in terms of pi.
Display Figures A, B, and C for all to see. Ask selected students to share their reasoning. Sequence the strategies from most calculations to most efficient.
If there were selected students who determined the areas were equal before calculating, ask them to share how they could tell. If there were no selected students, ask the class how we could determine that the area of the shaded regions in Figures A, B, and C were equal before calculating the answer of 30.96.
Next, focus the discussion on leaving answers in terms of \(\pi\) for each figure. Explain to students that in Figure A, the radius of the circle is 6, so the area of the circular region is \(\pi \boldcdot 6^2\). Instead of multiplying by an approximation of \(\pi\), we can express this answer as \(36\pi\). This is called answering in terms of \(\pi\). Consider writing “\(36\pi\)” inside the large circle of Figure A.
Discuss:
- In terms of \(\pi\), what is the area of one of the circular regions in Figure B? (\(9\pi\))
- What is the combined area of all four circles in Figure B? (\(4 \boldcdot 9\pi\), or \(36\pi\))
- What is the area of one of the circular regions in Figure C? (\(4\pi\))
- What is the combined area of all nine circles in Figure C? (\(9 \boldcdot 4\pi\), or \(36\pi\))
Consider writing “\(9\pi\)” and “\(4\pi\)” inside some of the circles in Figures B and C. Explain that the area of the shaded region for each of these figures is \(144 - 36\pi\).

Discuss how students' strategies differed between the first problem (about Figures A, B, and C) and the second problem (about Figures D and E) and why.
Ask students to express the area of Figures D and E in terms of \(\pi\). Record and display their answers of \(2 + 2\pi\) and \(4 + 1.5\pi\) for all to see. Ask students to discuss how they can tell Figure E’s area is larger than Figure D’s area when they are both written in terms of \(\pi\).
Design Principles(s): Optimize output (for explanation); Maximize meta-awareness
9.3: The Running Track Revisited (10 minutes)
Optional activity
Earlier in this lesson, students found the area of regions around circles and the area of fractions of circles in separate problems. In this activity, students combine these two strategies to find the area of a complex real-world object. Students engage in MP2 as they decide how to decompose the running track into measurable pieces and how to use the given information about the dimensions of the track to calculate areas.
Launch
Arrange students in groups of 2. Give students 3–4 minutes of partner work time followed by small-group and whole-class discussions.
Supports accessibility for: Language; Organization
Student Facing
The field inside a running track is made up of a rectangle 84.39 m long and 73 m wide, together with a half-circle at each end. The running lanes are 9.76 m wide all the way around.
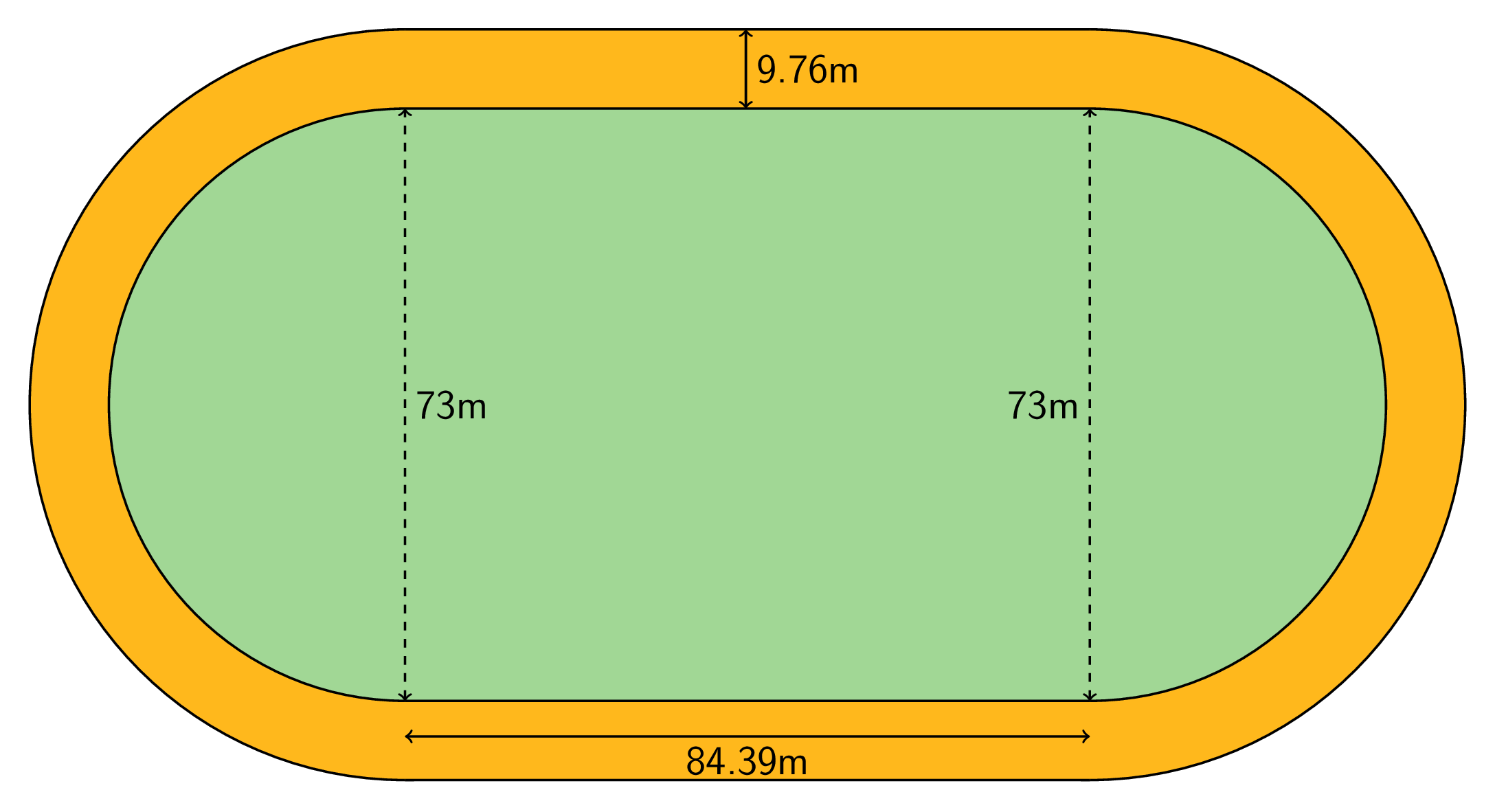
What is the area of the running track that goes around the field? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may think they can calculate the area of the running track by multiplying half of the perimeter times the radius, as if the shape were just a circle. Prompt them to see that they need to break the overall shape into rectangular and circular pieces.
Activity Synthesis
Pair the groups of 2 to create groups of 4. Have students compare answers and explain their reasoning until they reach an agreement.
As a whole group, discuss how finding the area of the track in this activity was similar or different to solving the two area problems in the previous activity. Make sure to highlight these points:
- Like the first problem in the previous activity, finding the area of the track can be done by finding the area of the larger shape (the track and the field inside) and then taking away the area of the field inside.
- Like the second problem in the previous activity, there are semicircles whose area can be found by composing them to make a full circle or by taking half the area of the corresponding full circle.
Design Principle(s): Cultivate conversation; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Discussion Questions:
- What is the area, in terms of \(\pi\), of a circle with a radius of 10? (\(100\pi\), because \(10^2=100\).)
- What is the area, in terms of \(\pi\), of a circle with a diameter of 10? (\(25\pi\), because \(10\div2=5\) and \(5^2=25\).)
- What is the area, in terms of \(\pi\), of a half-circle with a diameter of 10? (\(12.5\pi\), because \(25\div2=12.5\).)
9.4: Cool-down - Area of an Arch (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The relationship between \(A\), the area of a circle, and \(r\), its radius, is \(A=\pi r^2\). We can use this to find the area of a circle if we know the radius. For example, if a circle has a radius of 10 cm, then the area is \(\pi \boldcdot 10^2\) or \(100\pi\) cm2. We can also use the formula to find the radius of a circle if we know the area. For example, if a circle has an area of \(49 \pi\) m2 then its radius is 7 m and its diameter is 14 m.
Sometimes instead of leaving \(\pi\) in expressions for the area, a numerical approximation can be helpful. For the examples above, a circle of radius 10 cm has area about 314 cm2. In a similar way, a circle with area 154 m2 has radius about 7 m.
We can also figure out the area of a fraction of a circle. For example, the figure shows a circle divided into 3 pieces of equal area. The shaded part has an area of \(\frac13 \pi r^2\).
