Lesson 2
Exploring Circles
2.1: How Do You Figure? (5 minutes)
Warm-up
This warm-up prompts students to compare two figures and use the characteristics of those figures to help them sketch a possible third figure that has various characteristics of each. It invites students to explain their reasoning and hold mathematical conversations (MP3), and allows you to hear how they use terminology and talk about figures and their properties before beginning the upcoming lessons on circles. There are many good answers to the question and students should be encouraged to be creative. Encourage students to use multiple geometrical properties to create their third figure. The grid is given to allow students the opportunity to discuss side lengths, find area and perimeter of Figure A, as well as estimate dimensions of Figure B.
Launch
Arrange students in groups of 2–4. Display the image of the two figures for all to see. Make sure students understand they are to draw a third Figure, C, that has features of both Figure A and B but more closely resembles Figure A. Give students 2 minutes of quiet think time to sketch Figure C and then time to share their thinking with their group. After everyone has conferred in groups, ask the group to share the characteristics used in generating different versions of Figure C, and to show an example of one of the sketches.
Student Facing
Here are two figures.

Figure C looks more like Figure A than like Figure B. Sketch what Figure C might look like. Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
After students have conferred in groups, invite each group to share the characteristics that were important to them in creating their third figure. Some important points to be brought out include
- Figure A is a polygon, and Figure B is not a polygon.
- Figure A has the same width and height while the height and width of Figure B are very different.
- The area of Figure A is 36 square units while the area of Figure B is about 30 square units.
- The perimeter of Figure A is 24 units. The perimeter of Figure B is hard to determine, but it is less, maybe about 22 units.
Encourage students to be as precise as possible as they describe why they chose the figure they drew.
Display the responses for all to see. Since there is no single correct answer to the question, attend to students’ explanations and ensure the reasons given are correct. During the discussion, prompt students to explain the meaning of any terminology they used. Also, press students on unsubstantiated claims.
2.2: Sorting Round Objects (20 minutes)
Activity
The purpose of this activity is to build on students’ prior experience with circles and help them refine their definition of a circle. First, students sort pictures of round objects based on whether or not they are circular. Then, they compare the size of the circles to begin a discussion of what aspects of a circle can be measured. Lastly, the teacher introduces the terms diameter, center, radius, and circumference, so students can identify these measurements in the pictures of the circular objects. When students focus on what shapes have in common and describe their common features (and the deviations of non-examples) to build a definition, they are expressing regularity in repeated reasoning (MP8).
Since all of the objects pictured are three dimensional and circles are not, encourage students to focus on the circular (and non circular) aspects of the objects. For example, the utility hole cover is actually a cylinder with a relatively short height, but the outline of the utility hole cover is circular. Some of the pictures could reasonably be placed into either category. For example, the outline of the pizza is not a complete circle, but the outline of a slice of pepperoni may be. The final categorization is not as important as students’ reasoning about what makes something a circle.
In the second-to-last question, the use of the words smallest and largest is purposefully vague to encourage students to reason about the measurable things in a circle. As they work, listen for: how students define size, the ways they determine the size, estimation strategies and any actual estimations, specifically diameter, radius, circumference, or area of the circle. These will all be important in the whole-group discussion.
You will need the Sorting Round Objects blackline master for this activity.
Launch
Arrange students in groups of 2–3. Distribute slips with the pictures of round objects. Give students 1 minute of quiet think time to come up with categories they could use to sort the objects pictured, followed by 1 minute to share their ideas with their partner. Select students to share their ideas for sorting the objects into 2 categories. After a student suggests they could be sorted by whether or not the objects are circular, instruct the students to do that.
Demonstrate how to conduct the sorting activity. Choose a student to act as your partner. Select one card and then explain to your partner why you think the object is or is not circular. Demonstrate productive ways to agree or disagree, e.g., by explaining your mathematical thinking, asking clarifying questions, etc.
After sorting is complete, pause their work for a quick whole-group discussion. Poll the class on which of the objects they sorted into the not circular category. Ask students to explain why each of these objects is not circular. Start a list titled “Characteristics of a Circle” displayed for all to see. For each reason students give as to why one of the objects is not circular, add the related characteristic of a circle onto your list. Here is a table showing sample responses. The first two columns show what could be mentioned in the discussion and the third column shows what could be added to your displayed list.
| picture(s) | reason it is not a circle | characteristic of a circle |
|---|---|---|
| clock | straight edges and vertices | round, no corners |
| rug | straight sides (and taller than it is wide) | no straight sides |
| boiled egg and platter | taller than they are wide | the same distance across in every direction: length, width, height, longest diagonal |
| pizza and speedometer | The outer edges would be circles if they went all of the way around, but they do not. | closed figure |
| basketball | encloses a three-dimensional region | encloses a two-dimensional region |
Next, instruct students to put the pictures of objects that are not circular off to the side and focus on the objects that are circular for the rest of the activity.
Student Facing
Your teacher will give you some pictures of different objects.
- How could you sort these pictures into two groups? Be prepared to share your reasoning.
- Work with your partner to sort the pictures into the categories that your class has agreed on. Pause here so your teacher can review your work.
- What are some characteristics that all circles have in common?
- Put the circular objects in order from smallest to largest.
- Select one of the pictures of a circular object. What are some ways you could measure the actual size of your circle?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
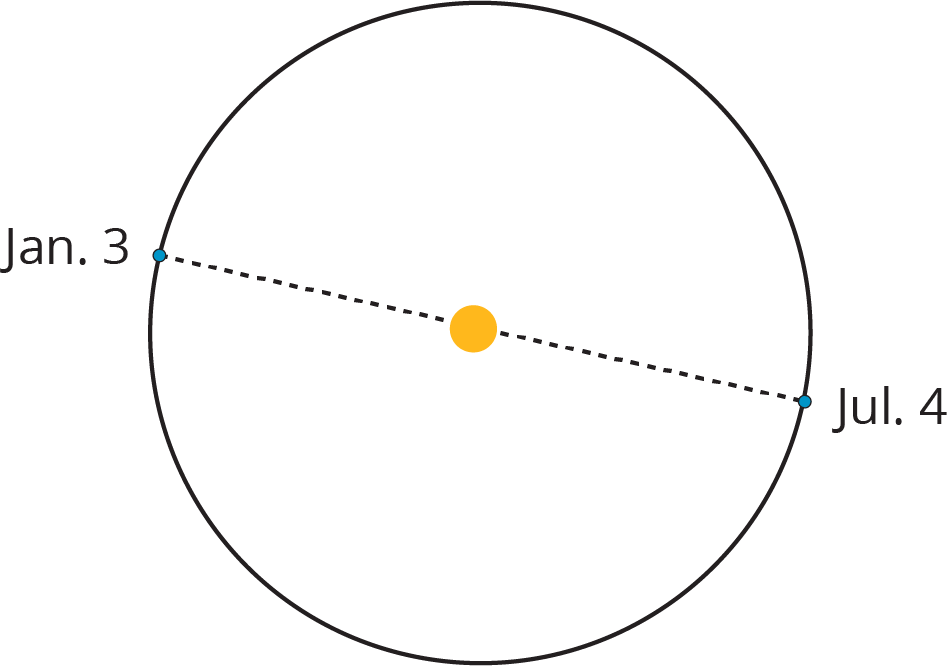
On January 3rd, Earth is 147,500,000 kilometers away from the Sun. On July 4th, Earth is 152,500,000 kilometers away from the Sun. The Sun has a radius of about 865,000 kilometers.
Could Earth’s orbit be a circle with some point in the Sun as its center? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may answer that the basketball is a circle, because the paper can only show a two-dimensional projection of the three-dimensional object. Tell them that a real basketball is a sphere, not a circle. If desired, prompt them to describe what aspect of a basketball is a circle. (The equator.)
Some students may think that the pizza and speedometer are circles, not paying attention to the fact that their circular outlines are not complete.
In the last part of the discussion, after introducing the terms, students may try to identify parts of a circle on the objects that were not circles. For example, they may think that the minute hand on the hexagonal clock represents the radius. Point out that the hand of the clock reaches closer to the midpoint of each edge than it does to each vertex, because the clock is not a circle.
Activity Synthesis
The goal of this final discussion is to introduce terms that describe measurable aspects of circles. Invite selected students to share their reasoning and estimates about the relative sizes of the circles. Make sure that students articulate which aspect of the objects are circles (for example, the outline of the utility hole cover or the path of the yo-yo trick), since all of the objects are actually three dimensional.
Ask students to defend their order by estimating how big each circle is. Wait for the ambiguity of “what part of the circle are we measuring” to come up, or point out that different students are (likely) using different attributes when discussing the size of the circle. Challenge students to explain themselves with more precision and then introduce the terms diameter, center, radius, and circumference as they relate to the parts being measured.
Some important points to cover include:
- Circles are one-dimensional figures that enclose a two-dimensional region.
- The size of a circle can be described using the length of its diameter—a segment with its endpoints on the circle that passes through the center. Any two diameters of the same circle have the same length. We will often use phrases like “What is the diameter of the circle?” to mean “What is the length of a diameter of the circle?”
- The circumference is the length around the circle.
- A radius is a line segment from the center of a circle to any point on the circle. Its length is half of the diameter.
Ask students to identify pictures from the activity that draw attention to the radius, to the diameter, and to the circumference, and ask how they decided. If students do not mention all examples, point them out:
- The radius is depicted in the wagon wheel, yo-yo trick, pivot irrigation, orange slice, dartboard, and airplane propeller.
- The diameter is depicted in the wagon wheel, dartboard, and grill.
- The circumference is depicted in all the circles but is especially prominent in the glow necklace and yo-yo trick.
Give students a minute to write down what each of the new terms means, using words or diagrams.
Lastly, display the picture of the grill, utility hole cover, or bike wheel for all to see. Draw students’ attention to some of the other lines (chords) that are not the diameter or the radius. Ask whether these lines depict the diameter or radius and why not.
Supports accessibility for: Memory; Language
2.3: Measuring Circles (5 minutes)
Activity
The purpose of this activity is to continue developing the idea that we can measure different attributes of a circle and to practice using the terms diameter, radius, and circumference. Students reason about these attributes when three different-sized circles are described as “measuring 24 inches” and realize that the 24 inches must measure a different attribute of each of the circles. Describing specifically which part of a circle is being measured is an opportunity for students to attend to precision (MP6).
Launch
Keep students in the same groups. Give students 2 minutes of quiet work time followed by partner discussion.
Supports accessibility for: Language; Organization
Student Facing
Priya, Han, and Mai each measured one of the circular objects from earlier.
- Priya says that the bike wheel is 24 inches.
- Han says that the yo-yo trick is 24 inches.
- Mai says that the glow necklace is 24 inches.
- Do you think that all these circles are the same size?
- What part of the circle did each person measure? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may think they are all the same size object because they are only focusing on the 24 inches. Ask students to describe each of the objects to make it clear they are not the same size.
Activity Synthesis
Ask one or more students to share their choices for diameter, radius, or circumference as the measurement of the three circles. Prompt students to explain their reasoning until they come to an agreement.
Display this image of the bike wheel and the airplane propeller to discuss the relationship between radius, \(r\), and diameter, \(d\), of a circle: \(d=2r\). When drawn to the same scale, the airplane propeller and bike wheel would look like this:
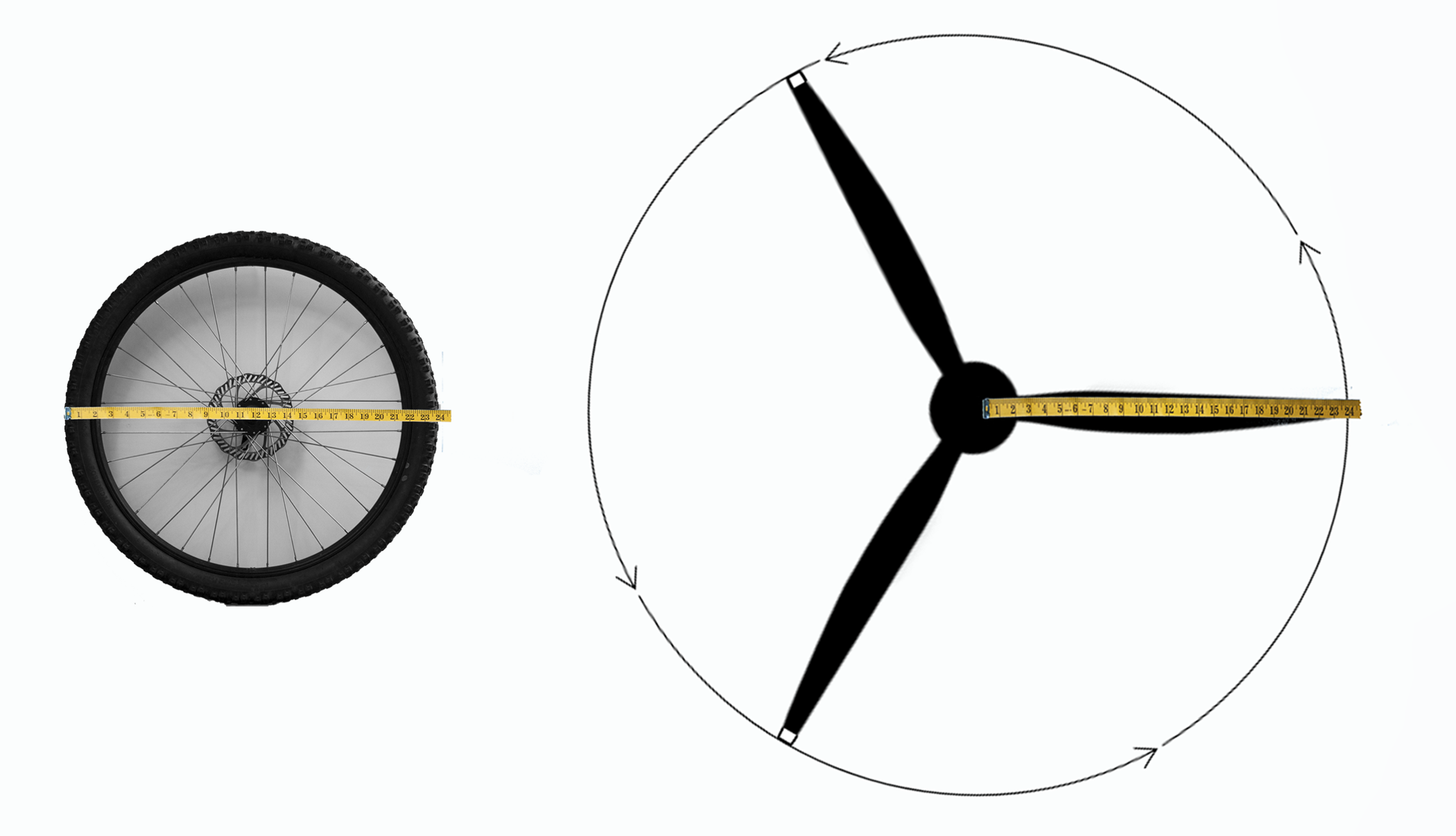
Future lessons will address the relationship between the circumference of a circle and the diameter.
Design Principle(s): Optimize output (for explanation)
2.4: Drawing Circles (10 minutes)
Optional activity
The purpose of this activity is to reinforce students’ understanding of the terms diameter, center, and radius and also for students to see what a compass is good for (MP5).
Before using the compass, students first attempt to draw a circle freehand. Then, they recognize the compass as a strategic tool for drawing circles. However, the compass is useful not just for drawing circles but also for transferring lengths from one location to another for many different purposes. Students will apply this understanding in later units, for example, when they construct a triangle given the lengths of its three sides. This activity prepares students for that application by asking them to make the radius of the circle match another length they have already drawn.
If this is a student’s first time using a compass, direct instruction may be needed on how to use one. The circles students draw may not be perfect, but as they gain more experience with a compass, they will improve. A digital version of the activity is provided for classrooms that do not have access to compasses but do have access to appropriate electronic devices.
As students work, monitor and select students who are correctly using the relationship between the diameter and radius to draw Circles C and D and other students who are recreating each of the different images from question 5 to share during the discussion.
Launch
Distribute rulers. Give students a few minutes of quiet work time for the first two questions. If a student asks for a circular object to trace, graph paper, a protractor, or a compass, make that available. After drawing Circles A and B, but before drawing Circles C and D, ask students “What was difficult about drawing the circles? How they could make their drawings more precise? and What tools might be helpful?” Once students realize that a compass would be a good tool for this task, distribute compasses to all students.
If using the digital activity, students will have the opportunity to create circles using an applet for questions 1–4. They will need a compass to complete question 5.
Supports accessibility for: Organization; Conceptual processing; Attention
Student Facing
Spend some time familiarizing yourself with the tools that are available in this applet.
Draw and label each circle.
- Circle A, with a diameter of 6 cm.
- Circle B, with a radius of 5 cm. Pause here so your teacher can review your work.
- Circle C, with a radius that is equal to Circle A’s diameter.
- Circle D, with a diameter that is equal to Circle B’s radius.
- Use a compass to recreate one of these designs.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Distribute rulers. Give students a few minutes of quiet work time for the first two questions. If a student asks for a circular object to trace, graph paper, a protractor, or a compass, make that available. After drawing Circles A and B, but before drawing Circles C and D, ask students “What was difficult about drawing the circles? How they could make their drawings more precise? and What tools might be helpful?” Once students realize that a compass would be a good tool for this task, distribute compasses to all students.
If using the digital activity, students will have the opportunity to create circles using an applet for questions 1–4. They will need a compass to complete question 5.
Supports accessibility for: Organization; Conceptual processing; Attention
Student Facing
Draw and label each circle.
- Circle A, with a diameter of 6 cm.
- Circle B, with a radius of 5 cm. Pause here so your teacher can review your work.
- Circle C, with a radius that is equal to Circle A’s diameter.
- Circle D, with a diameter that is equal to Circle B’s radius.
- Use a compass to recreate one of these designs.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students might think that they need a protractor to draw a circle. Allow them access to one. They may trace the outline of the protractor twice with tracings of straight sides coinciding. Ask them whether their traced shape meets all of the characteristics of a circle that were listed in the previous activity.
Once students start using the compasses, they may draw a circle with a radius of 6 cm instead of a diameter of 6 cm for Circle A. Remind them what diameter means and ask them to measure the diameter of their circle. When they realize it is incorrect for Circle A, tell them not to erase it yet. They might realize later that this is the answer for Circle C.
When recreating the given designs, students might struggle to know where to place their compasses. For the first design, the non-pencil end of the compass stays in the same place the whole time. For the second, third, and fourth designs, guide students to think about where to put the non-pencil end so that the circles will end up where they should go. For the second and fourth design, they should line up the pencil end of the compass on a point on the circle(s) they have already drawn. Similarly for the third design, students should line up the non-pencil end of the compass on a point of the circle(s) they have already drawn.
Activity Synthesis
The main goal for this discussion is for students to connect their use of a compass to the fact that any point on a circle is the same distance from the center.
Ask selected students to share their strategies for drawing Circles C and D. Highlight the relationship that \(d \div 2 = r\) for diameter \(d\) and radius \(r\) after each.
Ask selected students who recreated the first design to display their drawing. Ask “What is the same about all of these circles? What is different?” Students should notice they all have the same center, but different radii, diameters, and circumferences, but if they do not, make it known.
Ask selected students who recreated the second, third, or fourth design to display their drawing and ask “What is the same about all of these circles? What is different?” They all have the same radius, diameter, and circumference, but different centers.
Design Principle(s): Cultivate conversation; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
The main ideas are:
- A circle consists of all points that are the same distance to a point called the center. Circles enclose a circular region.
- Measurable attributes of a circle include: radius, diameter, circumference, and its enclosed area.
- We can draw a circle using a compass if we know the radius or diameter.
Since all radii of a circle have the same length, all diameters of a circle also have the same length: \(d = 2r\) if \(d\) represents the diameter and \(r\) represents the radius.
Discussion questions:
- Show one example of a circle and one of a non-circle and ask “Why is this a circle and this is not?”
- “How can we measure the size of a circle?”
- “What can a compass help us do?”
2.5: Cool-down - Comparing Circles (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
A circle consists of all of the points that are the same distance away from a particular point called the center of the circle.
A segment that connects the center with any point on the circle is called a radius. For example, segments \(QG\), \(QH\), \(QI\), and \(QJ\) are all radii of circle 2. (We say one radius and two radii.) The length of any radius is always the same for a given circle. For this reason, people also refer to this distance as the radius of the circle.
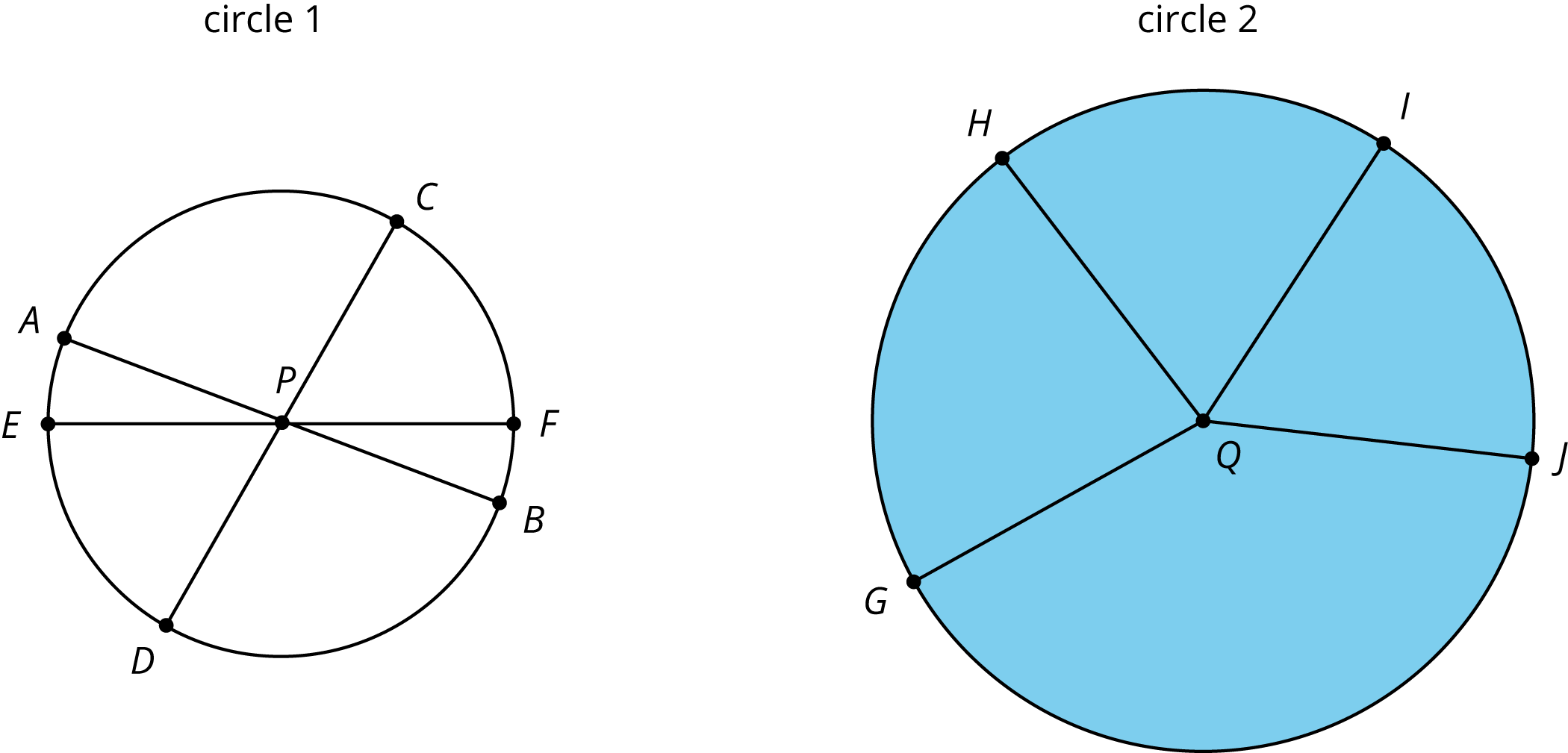
A segment that connects two opposite points on a circle (passing through the circle’s center) is called a diameter. For example, segments \(AB\), \(CD\), and \(EF\) are all diameters of circle 1. All diameters in a given circle have the same length because they are composed of two radii. For this reason, people also refer to the length of such a segment as the diameter of the circle.
The circumference of a circle is the distance around it. If a circle was made of a piece of string and we cut it and straightened it out, the circumference would be the length of that string. A circle always encloses a circular region. The region enclosed by circle 2 is shaded, but the region enclosed by circle 1 is not. When we refer to the area of a circle, we mean the area of the enclosed circular region.