Lesson 10
Distinguishing Circumference and Area
10.1: Filling the Plate (5 minutes)
Warm-up
This warm-up prompts students to apply what they have learned about finding the area of a circle to estimating the area of a circular plate in terms of a smaller circle. Students see a plate with a single cheese puff and from this information need to make a reasoned estimate for the number of cheese puffs that will cover the plate. As students discuss their estimates with a partner, monitor the discussions. Select students who use different estimation strategies to share during the discussion.
This activity was inspired by one created by Andrew Stadel. https://estimation180.com/day-207/
Launch
Arrange students in groups of 2. Show them the picture of the plate with one cheese puff and ask them what they notice and wonder.

Let students share their observation and question with one another and invite a few students to share with the class. If the question “How many cheese puffs will fit on the plate” does not come up, ask if any one wondered how many cheese puffs can fit on the plate. Give students two minutes to make an estimate.
Student Facing
About how many cheese puffs can fit on the plate in a single layer? Be prepared to explain your reasoning.

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite selected students to share their estimates and any information in the image that informs their estimates. After each explanation, solicit questions from the class that could help the student clarify his or her reasoning. Record the estimates and strategies and display them for all to see.
10.2: Card Sort: Circle Problems (15 minutes)
Activity
The purpose of this activity is for students to think about how circumference and area of circles apply to real-world situations. First, students sort slips based on whether the question is related to the circumference or area of a circle. Next, each group focuses on one of the questions (#1 through 5). They estimate appropriate measurements for the context, and use these measurements to calculate a reasonable answer (MP2). Questions 6 through 8 will be examined more closely in a future activity.
You will need the blackline master for this activity.
Launch
Arrange students in groups of 2. Explain or show images of any of the contexts that may be unfamiliar to your students.
Distribute question slips. Give students 3–4 minutes of partner work time to sort the question slips. Pause to poll the class on how they sorted each card. After students have come to an agreement on the sorting, assign each group one card from #1–5 to investigate further. Give students quiet work time to make their estimates and calculations, followed by small-group and whole-class discussion.
Supports accessibility for: Conceptual processing; Organization
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
Your teacher will give you cards with questions about circles.
- Sort the cards into two groups based on whether you would use the circumference or the area of the circle to answer the question. Pause here so your teacher can review your work.
- Your teacher will assign you a card to examine more closely. What additional information would you need in order to answer the question on your card?
- Estimate measurements for the circle on your card.
- Use your estimates to calculate the answer to the question.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students are confused about the difference between circumference and area, remind them that circumference measures distance around a circle and uses linear units, while area measures the inside of a circle and uses square units.
Students might think they need to solve the problems on all 8 cards. Point out that the first question is only asking them to think about how they would solve the problems, not to do any actual calculations.
For the horse walker problem, students might not realize that they need to convert 1 mile to the same units as their estimated diameter, or that they need to divide by the circumference.
Activity Synthesis
The goal of this discussion is for students to articulate how they decide whether an answer is reasonable.
First, have the students who worked on the same question compare answers and strategies. Display these questions to guide their group discussions:
- Did you use the same units?
- How did you come up with your estimate for the size of the circle (radius or diameter)?
- Are your estimates very close? Are they reasonable?
- How did you calculate your answer to the question?
- Are your answers very close? Are they reasonable?
Next, invite students who have different answers to the same question to share their reasoning with the class. For each group, ask the rest of the class “Which of these answers do you think are reasonable? Why?” Make sure students understand that since estimates were called for, there is not one exact correct answer for each of these problems.
Some mistakes that could lead to an unreasonable answer include:
- Making too inaccurate of an initial estimate about the size of the circle
- Using the diameter as if it were the radius, or vice versa
- Using the wrong formula for circumference or area
- Forgetting to address an aspect of the question (such as finding the area of the entire pizza, not one slice)
- Labeling the units incorrectly, like using feet for a measure of area instead of square feet
- Reporting an answer with more decimals places than is reasonable given the level of precision of their initial estimates
If not mentioned by students, look for opportunities to bring these up, in preparation for a future activity in which students will analyze claims made about questions #6–8.
10.3: Visual Display of Circle Problem (15 minutes)
Optional activity
This activity asks students to create a visual display of the circle problem that they solved previously. They can practice explaining their reasoning more clearly on this display than they did in the previous activity. This gives them an opportunity to organize and record their information in a way that can be shared with others who worked on a different problem. The displays can also serve as a record of reasoning about circles which can be referred back to later in the year.
Launch
Keep students in the same groups. Explain that they are going to create a visual display of the circle problem that they just worked on. Follow with discussion.
Supports accessibility for: Organization; Attention
Student Facing
In the previous activity you estimated the answer to a question about circles.
Create a visual display that includes:
- The question you were answering
- A diagram of a circle labeled with your estimated measurements
- Your thinking, organized so that others can follow it
- Your answer, expressed in terms of \(\pi\) and also expressed as a decimal approximation
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Arrange for groups that are assigned the same problem to present their visual displays near one another. Give students a few minutes to visit the displays and to see the estimates others used to answer the question. Before students begin a gallery walk, ask them to be prepared to share a couple of observations about how their estimates and strategies are the same as or different from others’.
After the gallery walk, invite a couple of students to share their observations.
10.4: Analyzing Circle Claims (10 minutes)
Activity
The purpose of this activity is for students to look more closely at the last three situations of the card sort activity (questions 6 through 8). They analyze and critique two claims about each situation, choosing or supplying the best response and explaining why (MP3). Students must recognize that in the first situation, one of the claims inaccurately estimates the size of the circle. In the second situation, one of the claims calculates the circumference instead of the area. In the third situation, both claims are inaccurate. One of the claims has the right number but uses square units, and the other has the right units but the wrong number.
As students work, monitor and select students who can explain why they agree with the correct claim and others who can explain why they disagree with the incorrect claim. For the third situation, select students who can explain why they disagree with both of the claims, even if they are unsure they are allowed to disagree with both.
Launch
Keep students in same groups. Tell students they are going to look at how some other students solved the questions on cards 6, 7, and 8. For the first situation, make sure students realize we are referring to the type of merry-go-round at a playground (as pictured in their books or devices), not the larger type of carousel they might see at a fair.
Supports accessibility for: Language; Organization
Student Facing
Here are two students’ answers for each question. Do you agree with either of them? Explain or show your reasoning.
-
How many feet are traveled by a person riding once around the merry-go-round?
- Clare says, “The radius of the merry-go-round is about 4 feet, so the distance around the edge is about \(8\pi\) feet.”
- Andre says, “The diameter of the merry-go-round is about 4 feet, so the distance around the edge is about \(4\pi\) feet.”
-
How much room is there to spread frosting on the cookie?

- Clare says “The radius of the cookie is about 3 centimeters, so the space for frosting is about \(6\pi\) cm2.”
- Andre says “The diameter of the cookie is about 3 inches, so the space for frosting is about \(2.25\pi\) in2.”
-
How far does the unicycle move when the wheel makes 5 full rotations?

- Clare says, “The diameter of the unicycle wheel is about 0.5 meters. In 5 complete rotations it will go about \(\frac52\pi\) m2.”
- Andre says, “I agree with Clare's estimate of the diameter, but that means the unicycle will go about \(\frac{5}{4}\pi\) m.”
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
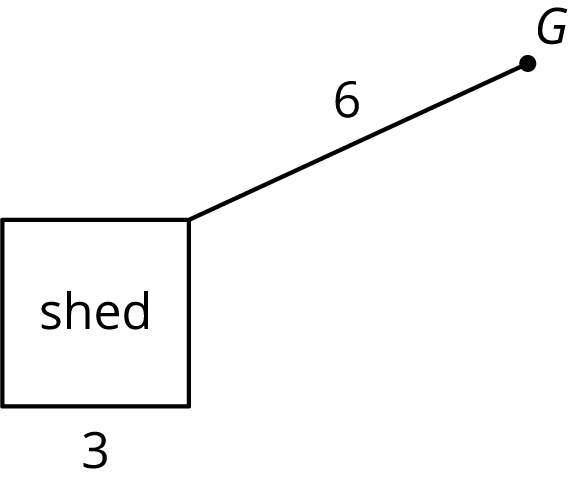
A goat (point \(G\)) is tied with a 6-foot rope to the corner of a shed. The floor of the shed is a square whose sides are each 3 feet long. The shed is closed and the goat can't go inside. The space all around the shed is flat, grassy, and the goat can't reach any other structures or objects. What is the area over which the goat can roam?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might multiply by a decimal approximation, without recognizing that the answers in the claims are all given in terms of \(\pi\).
Students might not realize there is an error with both of the claims in the third question.
Finally, students might not realize that they are supposed to analyze the reasonableness of the estimates, not just the mathematical correctness of the calculations.
Activity Synthesis
For each situation, poll the class on which person’s claim is more accurate. Ask selected students to share their reasoning for each claim. If it does not come out during the discussion, point out that the formula for the area of a circle has a squared term and the units of the answer are square units, while the formula for the circumference does not have a squared term and the units of the answer are linear units.
Note: It is not possible to know for certain what Clare or Andre were thinking when they made their calculations. For example, it is likely in the second problem that Clare found the circumference of the cookie instead of its area, but it is not possible to know. Interpreting the work of others (to the extent possible) is an important skill and a fundamental part of MP3. A wide range of interpretations need to be considered, always keeping an open mind.
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
Discussion Questions:
- When would we need to calculate the circumference of a circle?
- When would we need to calculate the area?
- What do you need to know to estimate or calculate the circumference of a circle? (radius or diameter)
- What do you need to know in order to estimate or calculate the area of a circle? (radius or diameter)
Consider posting the students’ displays from the card sorting activity, grouped by circumference or area, so students can refer to them later.
10.5: Cool-down - Measuring a Circular Lawn (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Sometimes we need to find the circumference of a circle, and sometimes we need to find the area. Here are some examples of quantities related to the circumference of a circle:
- The length of a circular path.
- The distance a wheel will travel after one complete rotation.
- The length of a piece of rope coiled in a circle.
Here are some examples of quantities related to the area of a circle:
- The amount of land that is cultivated on a circular field.
- The amount of frosting needed to cover the top of a round cake.
- The number of tiles needed to cover a round table.
In both cases, the radius (or diameter) of the circle is all that is needed to make the calculation. The circumference of a circle with radius \(r\) is \(2\pi r\) while its area is \(\pi r^2\). The circumference is measured in linear units (such as cm, in, km) while the area is measured in square units (such as cm2, in2, km2).
