Lesson 3

Exploring Circumference

View Student Lesson

Problem 1

Diego measured the diameter and circumference of several circular objects and recorded his measurements in the table.

object diameter (cm) circumference (cm)
half dollar coin 3 10
flying disc 23 28
jar lid 8 25
flower pot 15 48

One of his measurements is inaccurate. Which measurement is it? Explain how you know.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Complete the table. Use one of the approximate values for \(\pi\) discussed in class (for example 3.14, \(\frac{22}{7}\), 3.1416). Explain or show your reasoning.

object diameter circumference
hula hoop 35 in
circular pond 556 ft
magnifying glass 5.2 cm
car tire 71.6 in

Solution

For access, consult one of our IM Certified Partners.

Problem 3

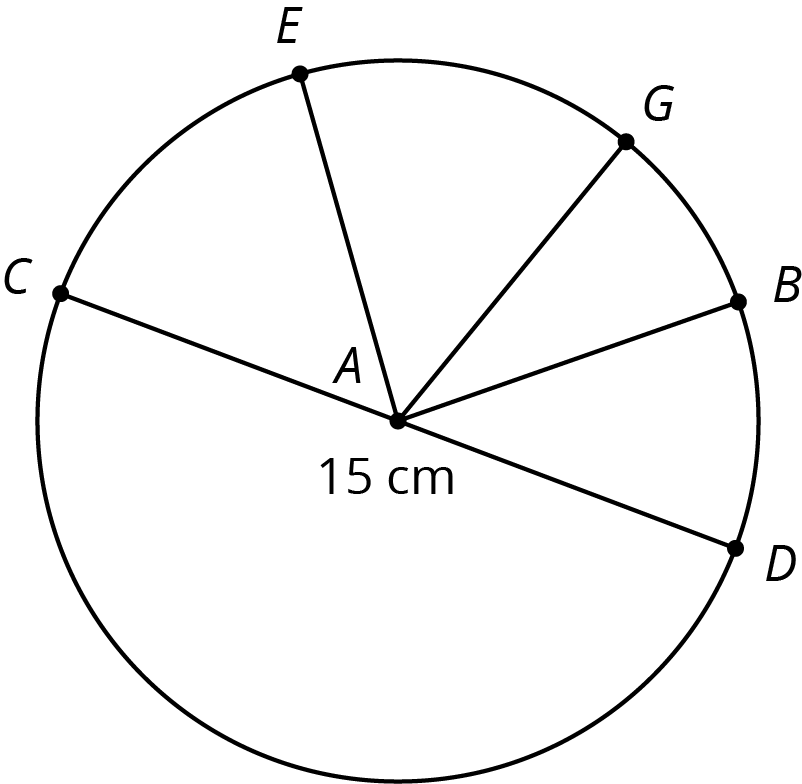
\(A\) is the center of the circle, and the length of \(CD\) is 15 centimeters.

  1. Name a segment that is a radius. How long is it?
  2. Name a segment that is a diameter. How long is it?
A circle with center point A. Diameter CD, 15 cm. Points on the circle are C, E, G, B, D.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 3, Lesson 2.)

Problem 4

  1. Consider the equation \(y=1.5x +2\). Find four pairs of \(x\) and \(y\) values that make the equation true. Plot the points \((x, y)\) on the coordinate plane.

    Blank grid, origin O. Horizontal axis, scale 0 to 7, by 1's. Vertical axis, scale 0 to 14, by 2's. 
  2. Based on the graph, can this be a proportional relationship? Why or why not?

Solution

For access, consult one of our IM Certified Partners.

(From Unit 2, Lesson 10.)