Lesson 11
Interpreting Graphs of Proportional Relationships
11.1: What Could the Graph Represent? (5 minutes)
Warm-up
This warm-up gives students an opportunity to think back to examples of proportional relationships they have encountered. Students are given a minute to think of some situations that could be represented by a graph. Several of their ideas should be shared with the class before students answer the remaining questions. During discussion, the characteristics of a graph of a proportional relationship should be reinforced.
Launch
Tell students that they will look at an unlabeled graph, and their job is to think of a situation that the graph could represent. Display the problem for all to see and give 1 minute of quiet think time. Ask students to give a signal when they have thought of a situation.
Invite some students to share their ideas and record the responses for all to see. (The purpose of this is to provide some inspiration to students who haven't come up with anything.) Ask students how they know all of the relationships are proportional. (Responses might include: when one value is 0 the other is 0, the situation involves equivalent ratios, or that any pair of values in the relationship has the same unit rate.)
Ask students to complete the rest of the questions.
Student Facing
Here is a graph that represents a proportional relationship.
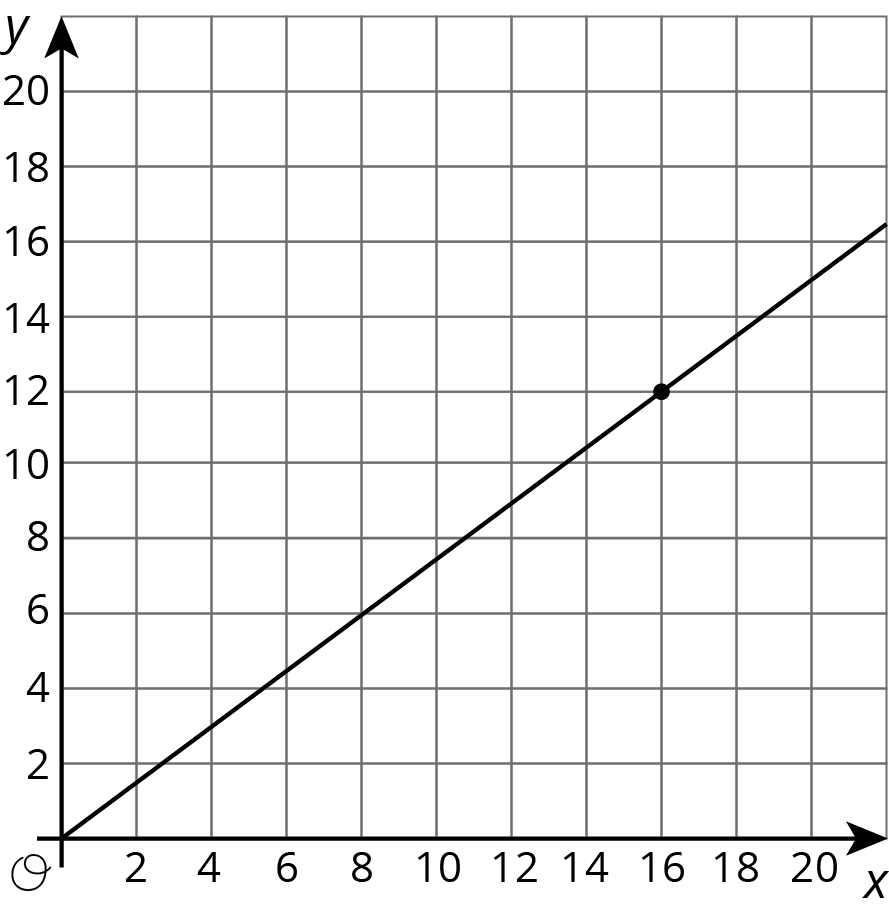
- Invent a situation that could be represented by this graph.
- Label the axes with the quantities in your situation.
- Give the graph a title.
- There is a point on the graph. What are its coordinates? What does it represent in your situation?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask a few students to share their situations and other responses. After each, ask the class if they need more information to understand the situation. After a few students have shared, ask the class to think about how all the situations were different and what they had in common. What sorts of things are always true about proportional relationships? Some possible responses might be:
- When one quantity is 0, the other is also 0.
- There is always the same amount of one quantity for every 1 of the other quantity.
- Context-specific considerations like constant speed, the same taste, or the same color.
Remind students that a coordinate point, \((x,y)\) is made up of the “\(x\)-coordinate” and the “\(y\)-coordinate.”
11.2: Tyler's Walk (15 minutes)
Activity
This activity is intended to further students’ understanding of the graphs of proportional relationships in the following respects:
- points on the graph of a proportional relationship can be interpreted in the context represented (MP2)
- for these points, the quotient of the coordinates is—excepting \((0,0)\)—the constant of proportionality
- if the first coordinate is 1, then the corresponding coordinate is \(k\), the constant of proportionality.
Students explain correspondences between parts of the table and parts of the graph. The graph is simple so that students can focus on what a point means in the situation represented. Students need to realize, however, that the axes are marked in 10-unit intervals. The discussion questions are opportunities for students to construct viable arguments and critique the reasoning of others (MP3).
Launch
Arrange students in groups of 2. Give students 5 minutes of quiet work time followed by students discussing responses with a partner, followed by whole-class discussion.
Supports accessibility for: Organization; Attention
Design Principle(s): Maximize meta-awareness; Support sense-making
Student Facing
Tyler was at the amusement park. He walked at a steady pace from the ticket booth to the bumper cars.
-
The point on the graph shows his arrival at the bumper cars. What do the coordinates of the point tell us about the situation?
- The table representing Tyler's walk shows other values of time and distance. Complete the table. Next, plot the pairs of values on the grid.
- What does the point \((0, 0)\) mean in this situation?
- How far away from the ticket booth was Tyler after 1 second? Label the point on the graph that shows this information with its coordinates.
- What is the constant of proportionality for the relationship between time and distance? What does it tell you about Tyler's walk? Where do you see it in the graph?
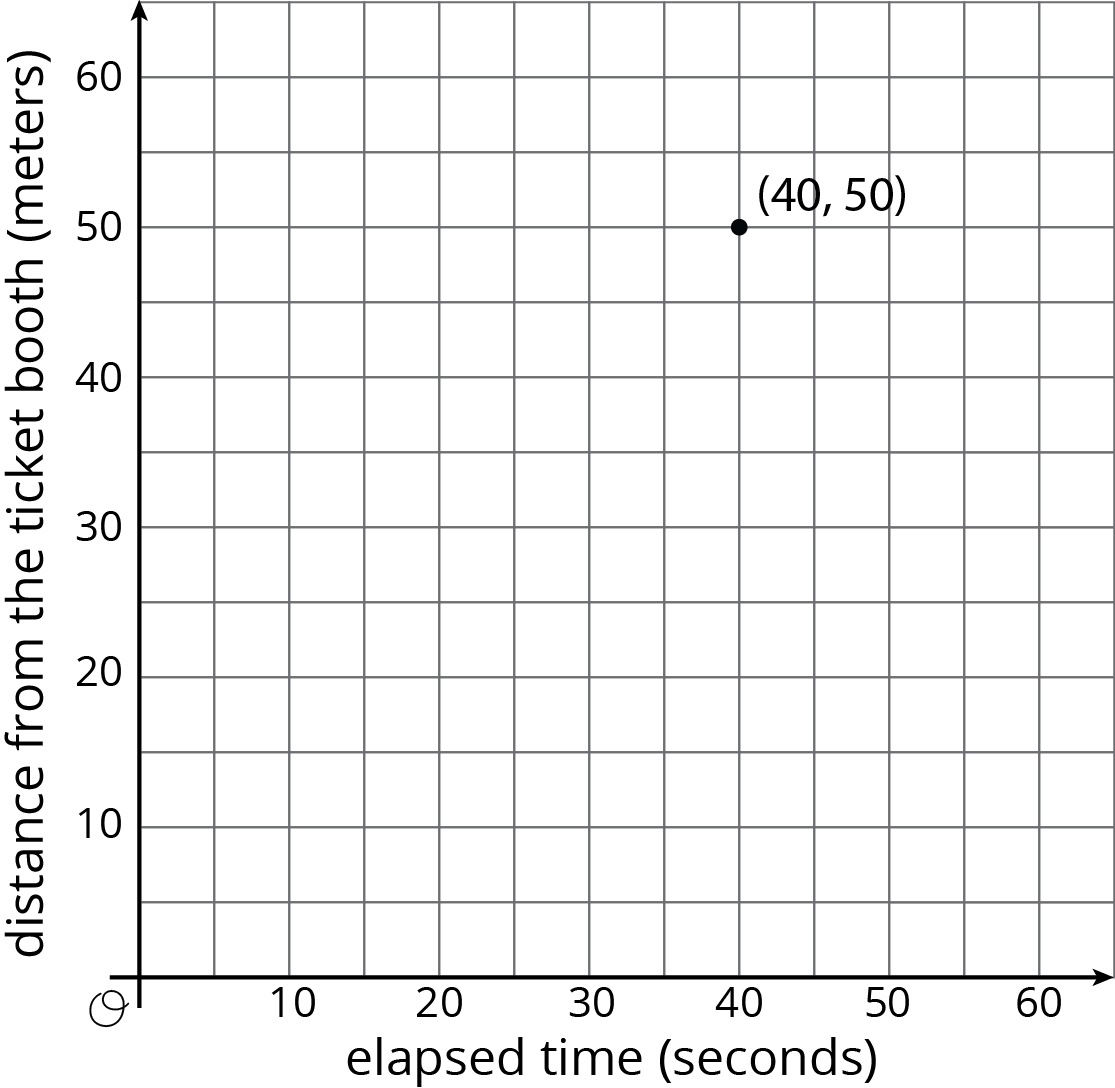
| time (seconds) |
distance (meters) |
|---|---|
| 0 | 0 |
| 20 | 25 |
| 30 | 37.5 |
| 40 | 50 |
| 1 |
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
If Tyler wanted to get to the bumper cars in half the time, how would the graph representing his walk change? How would the table change? What about the constant of proportionality?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
These questions can be used for discussion or for students who need scaffolding.
- "What quantities are shown in the graph?" (Distance in meters that Tyler is from the ticket booth and time elapsed in seconds since he started walking.)
- "How far is the ticket booth from the bumper cars?" (50 meters, assuming that Tyler walked in a straight line.) This is an opportunity for attention to precision (MP6) and making explicit assumptions about a situation (MP4).
- "Do the values in your table show a proportional relationship? How do you know?" (Based on prior lessons in this unit, students should identify the relationship as proportional because for every point the unit rate is the same.)
- "What do the coordinates of the points on the graph show?" (The first coordinate gives amount of time in seconds that elapsed since Tyler started walking. Its corresponding second coordinate shows how many meters away from the ticket booth Tyler was at the corresponding time, assuming that Tyler walked in a straight line.)
Activity Synthesis
After students work on the task, it is important to discuss how the axis labels and the description in the task statement help us interpret points on the graph.
Consider asking these questions:
- "What quantities are shown in the graph?" (Distance in meters that Tyler is from the ticket booth and time elapsed in seconds since he started walking.)
- "How far is the ticket booth from the bumper cars?" (50 meters, assuming that Tyler walked in a straight line.) This is an opportunity for attention to precision (MP6) and making explicit assumptions about a situation (MP4).
- "Do the values in your table show a proportional relationship? How do you know?" (Based on prior lessons in this unit, students should identify the relationship as proportional because for every point the unit rate is the same.)
- "What do the coordinates of the points on the graph show?" (The first coordinate gives amount of time in seconds that elapsed since Tyler started walking. Its corresponding second coordinate shows how many meters away from the ticket booth Tyler was at the corresponding time, assuming that Tyler walked in a straight line.)
Ask students for the equation of this proportional relationship. Finally ask where students see \(k\), the constant of proportionality, in each representation, the equation, the graph, the table, and the verbal description of the situation.
11.3: Seagulls Eat What? (15 minutes)
Activity
In this activity, make sure students understand what it means when we draw a solid line instead of just points in a straight line to represent the proportional relationship.
Launch
Keep students in the same groups of 2. Give 5 minutes of quiet work time followed by partner and whole-class discussion.
Design Principle(s): Optimize output (for justification); Maximize meta-awareness
Student Facing
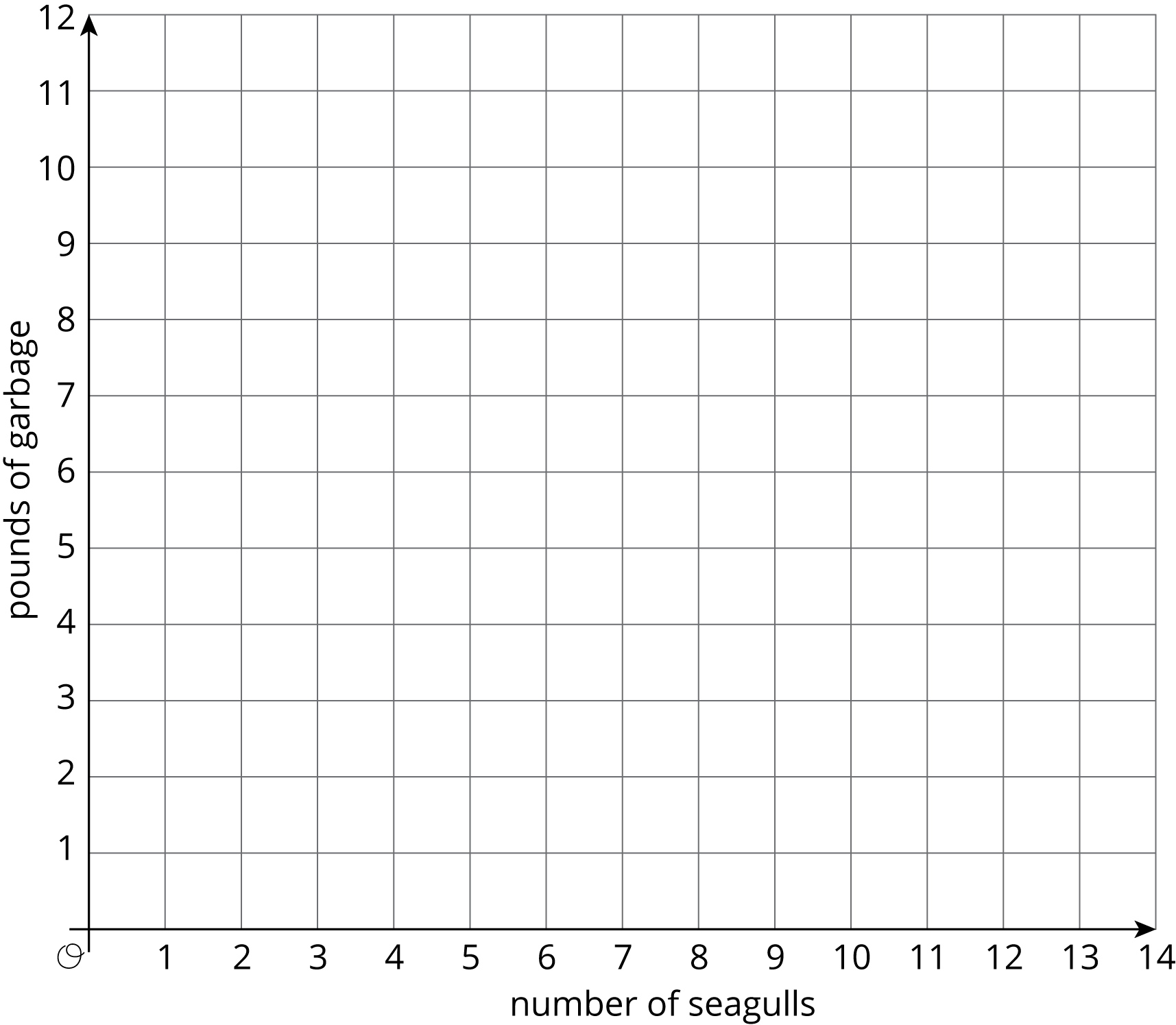
4 seagulls ate 10 pounds of garbage. Assume this information describes a proportional relationship.
- Plot a point that shows the number of seagulls and the amount of garbage they ate.
- Use a straight edge to draw a line through this point and \((0,0)\).
- Plot the point \((1, k)\) on the line. What is the value of \(k\)? What does the value of \(k\) tell you about this context?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Keep students in the same groups of 2. Give 5 minutes of quiet work time followed by partner and whole-class discussion.
Design Principle(s): Optimize output (for justification); Maximize meta-awareness
Student Facing
4 seagulls ate 10 pounds of garbage. Assume this information describes a proportional relationship.
- Plot a point that shows the number of seagulls and the amount of garbage they ate.
- Use a straight edge to draw a line through this point and \((0,0)\).
- Plot the point \((1, k)\) on the line. What is the value of \(k\)? What does the value of \(k\) tell you about this context?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to find \(k\), encourage them to create a table with a few rows in it and ask them how they can use the table to find \(k\).
Activity Synthesis
Invite students to share their value and interpretation of \(k\). Ask them for different ways to express this information. (Each seagull eats 2.5 pounds of garbage. Or: The rate of garbage consumption is 2.5 pounds per seagull.)
Ask students if it is possible to interpret the meaning of each point on the solid line. (No, only whole numbers of seagulls make sense.) Ask, why it is still useful to draw in the line. "How can it help us to learn more about the situation?" (It helps us to easily find out how much garbage different numbers of seagulls eat. It also helps us to estimate the value of \(k\).)
Lesson Synthesis
Lesson Synthesis
Revisit the key insights from this lesson:
- We can interpret points on a graph in terms of the context it represents.
- The \(y\)-value that goes with the \(x\)-value of 1 is special because it shows us the value of the constant of proportionality. It can be seen using a table or a graph.
Display the completed graph from one of the activities. Choose a point on the graph and ask students to interpret its coordinates in the situation. Then choose the point with \(x\)-coordinate 1 and ask about the significance of its \(y\)-coordinate.
11.4: Cool-down - Filling a Bucket (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
For the relationship represented in this table, \(y\) is proportional to \(x\). We can see in the table that \(\frac54\) is the constant of proportionality because it’s the \(y\) value when \(x\) is 1.
The equation \(y = \frac54 x\) also represents this relationship.
| \(x\) | \(y\) |
|---|---|
| 4 | 5 |
| 5 | \(\frac{25}{4}\) |
| 8 | 10 |
| 1 | \(\frac{5}{4}\) |
Here is the graph of this relationship.
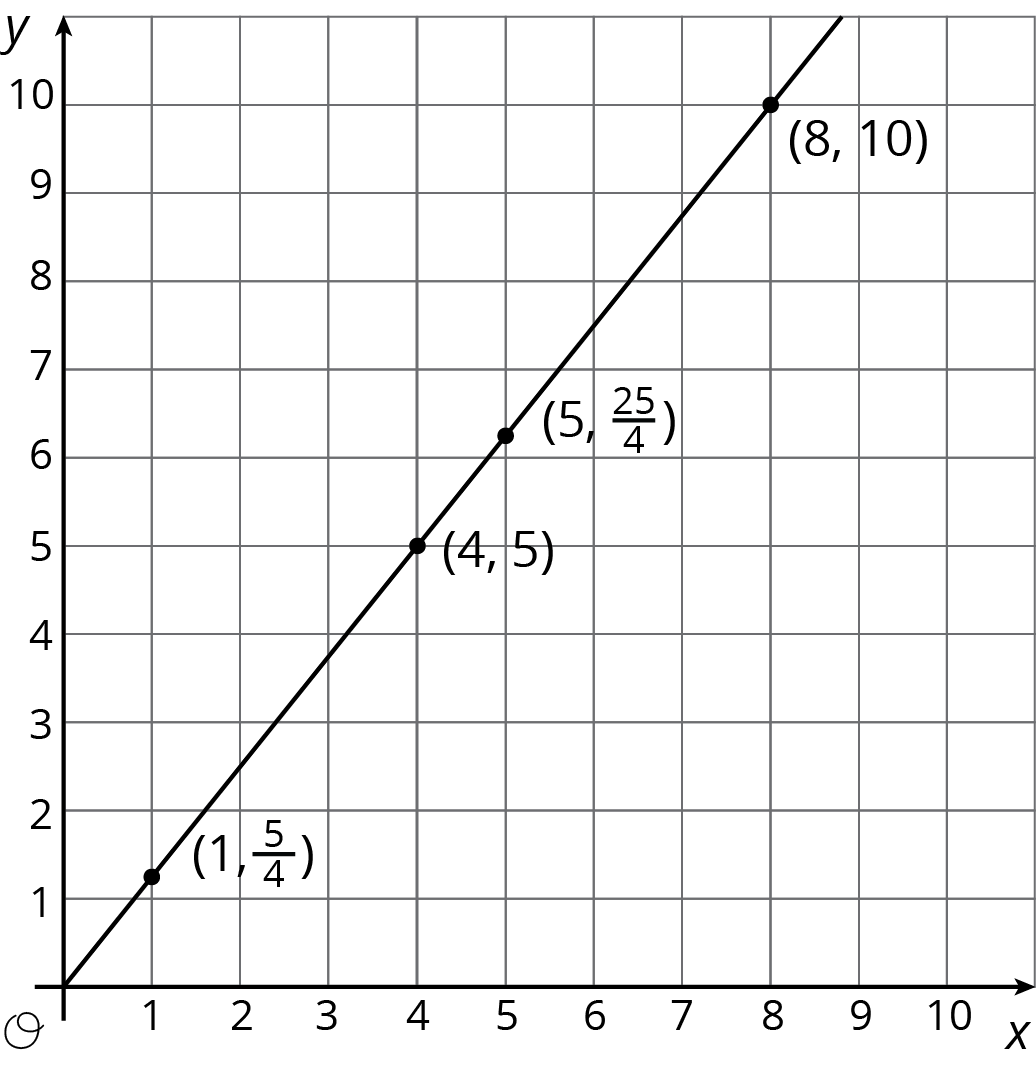
If \(y\) represents the distance in feet that a snail crawls in \(x\) minutes, then the point \((4, 5)\) tells us that the snail can crawl 5 feet in 4 minutes.
If \(y\) represents the cups of yogurt and \(x\) represents the teaspoons of cinnamon in a recipe for fruit dip, then the point \((4, 5)\) tells us that you can mix 4 teaspoons of cinnamon with 5 cups of yogurt to make this fruit dip.
We can find the constant of proportionality by looking at the graph, because \(\frac54\) is the \(y\)-coordinate of the point on the graph where the \(x\)-coordinate is 1. This could mean the snail is traveling \(\frac54\) feet per minute or that the recipe calls for \(1\frac14\) cups of yogurt for every teaspoon of cinnamon.
In general, when \(y\) is proportional to \(x\), the corresponding constant of proportionality is the \(y\)-value when \(x=1\).