Lesson 11
Interpreting Graphs of Proportional Relationships
Let’s read stories from the graphs of proportional relationships.
11.1: What Could the Graph Represent?
Here is a graph that represents a proportional relationship.
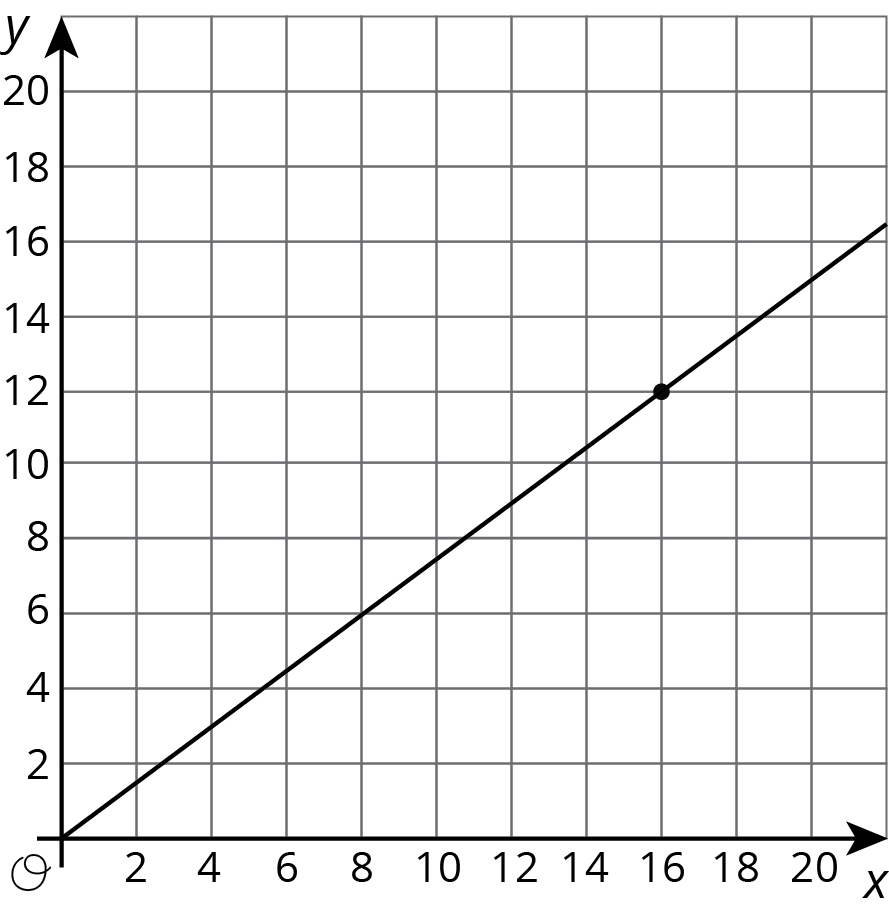
- Invent a situation that could be represented by this graph.
- Label the axes with the quantities in your situation.
- Give the graph a title.
- There is a point on the graph. What are its coordinates? What does it represent in your situation?
11.2: Tyler's Walk
Tyler was at the amusement park. He walked at a steady pace from the ticket booth to the bumper cars.
-
The point on the graph shows his arrival at the bumper cars. What do the coordinates of the point tell us about the situation?
- The table representing Tyler's walk shows other values of time and distance. Complete the table. Next, plot the pairs of values on the grid.
- What does the point \((0, 0)\) mean in this situation?
- How far away from the ticket booth was Tyler after 1 second? Label the point on the graph that shows this information with its coordinates.
- What is the constant of proportionality for the relationship between time and distance? What does it tell you about Tyler's walk? Where do you see it in the graph?
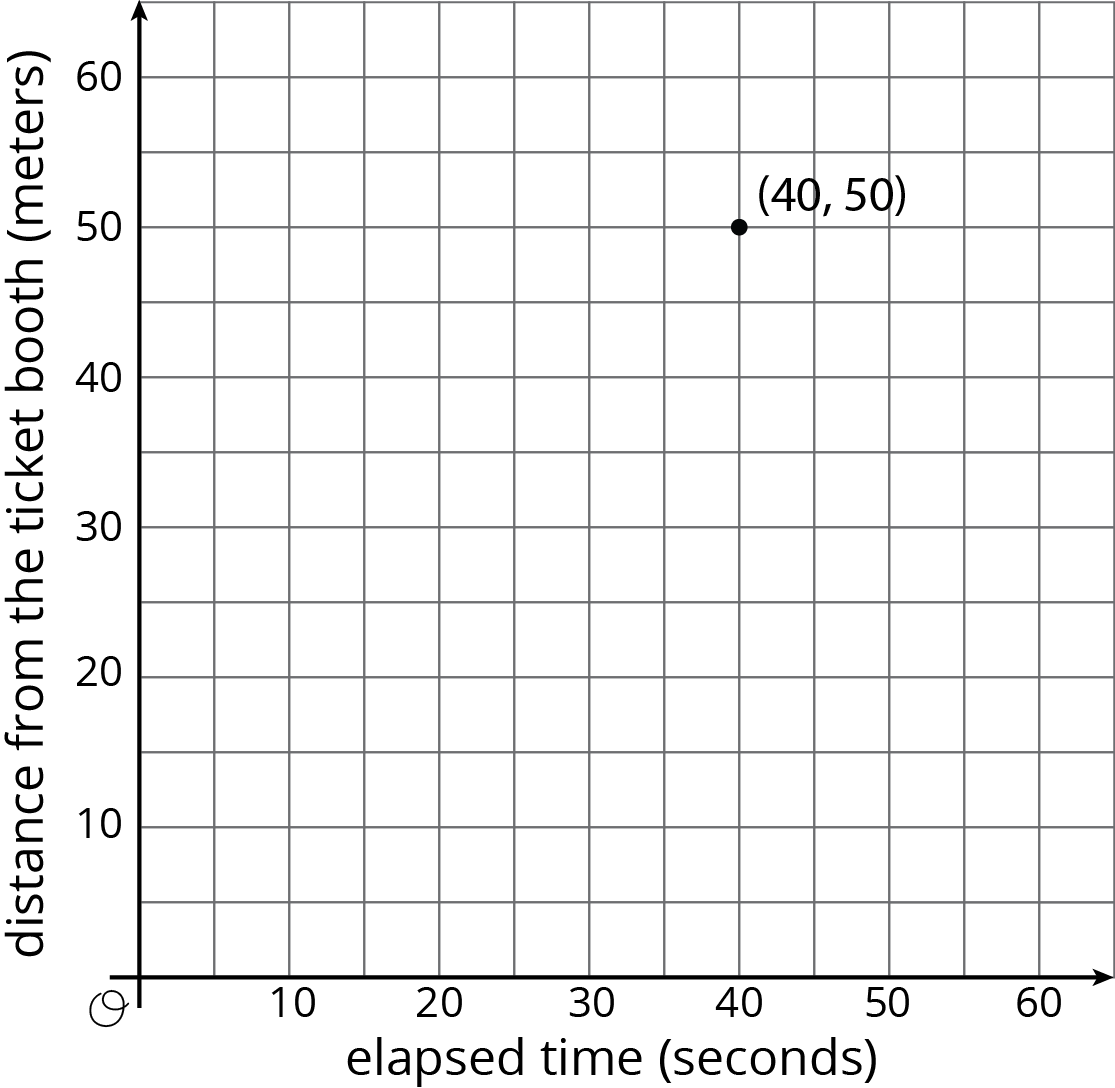
| time (seconds) |
distance (meters) |
|---|---|
| 0 | 0 |
| 20 | 25 |
| 30 | 37.5 |
| 40 | 50 |
| 1 |
If Tyler wanted to get to the bumper cars in half the time, how would the graph representing his walk change? How would the table change? What about the constant of proportionality?
11.3: Seagulls Eat What?
4 seagulls ate 10 pounds of garbage. Assume this information describes a proportional relationship.
- Plot a point that shows the number of seagulls and the amount of garbage they ate.
- Use a straight edge to draw a line through this point and \((0,0)\).
- Plot the point \((1, k)\) on the line. What is the value of \(k\)? What does the value of \(k\) tell you about this context?
Summary
For the relationship represented in this table, \(y\) is proportional to \(x\). We can see in the table that \(\frac54\) is the constant of proportionality because it’s the \(y\) value when \(x\) is 1.
The equation \(y = \frac54 x\) also represents this relationship.
| \(x\) | \(y\) |
|---|---|
| 4 | 5 |
| 5 | \(\frac{25}{4}\) |
| 8 | 10 |
| 1 | \(\frac{5}{4}\) |
Here is the graph of this relationship.
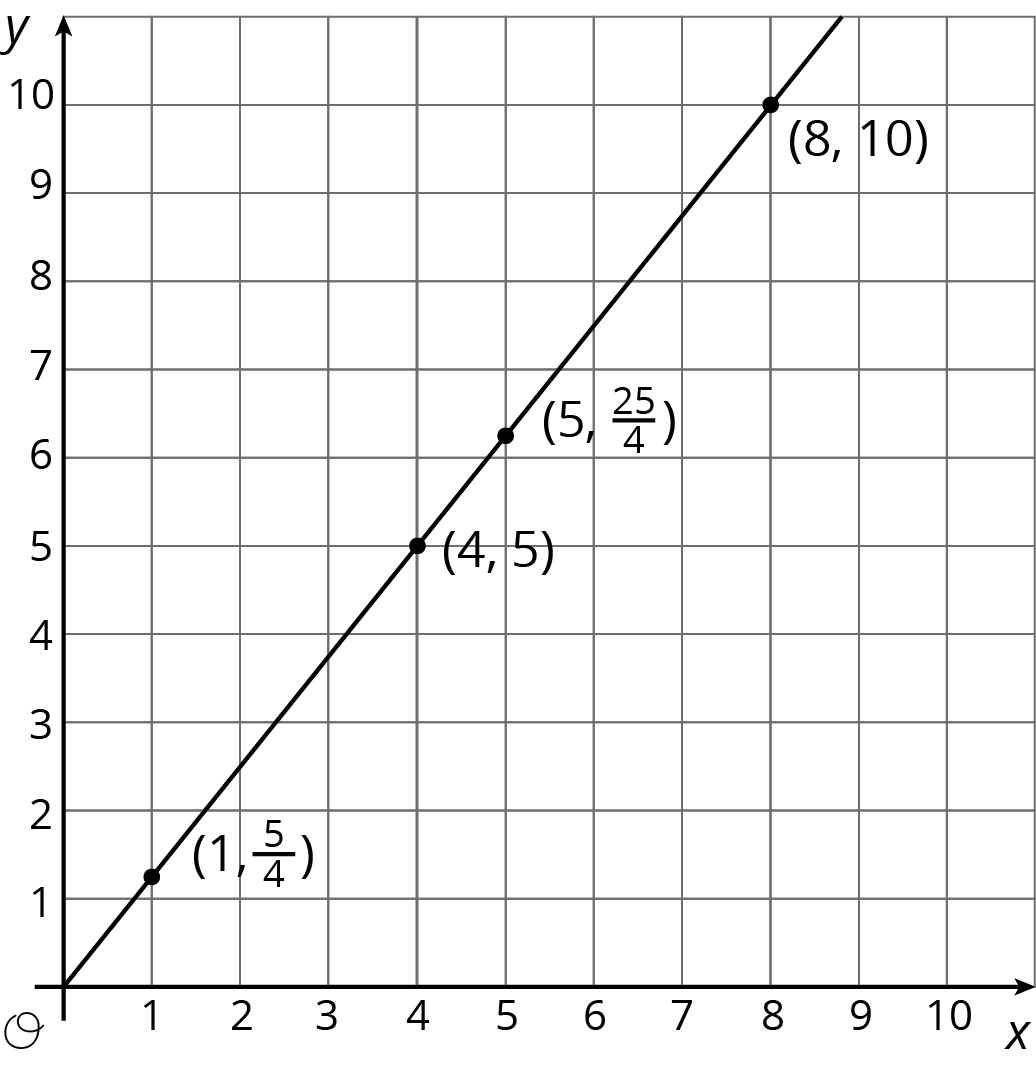
If \(y\) represents the distance in feet that a snail crawls in \(x\) minutes, then the point \((4, 5)\) tells us that the snail can crawl 5 feet in 4 minutes.
If \(y\) represents the cups of yogurt and \(x\) represents the teaspoons of cinnamon in a recipe for fruit dip, then the point \((4, 5)\) tells us that you can mix 4 teaspoons of cinnamon with 5 cups of yogurt to make this fruit dip.
We can find the constant of proportionality by looking at the graph, because \(\frac54\) is the \(y\)-coordinate of the point on the graph where the \(x\)-coordinate is 1. This could mean the snail is traveling \(\frac54\) feet per minute or that the recipe calls for \(1\frac14\) cups of yogurt for every teaspoon of cinnamon.
In general, when \(y\) is proportional to \(x\), the corresponding constant of proportionality is the \(y\)-value when \(x=1\).
Glossary Entries
- coordinate plane
The coordinate plane is a system for telling where points are. For example. point \(R\) is located at \((3, 2)\) on the coordinate plane, because it is three units to the right and two units up.

- origin
The origin is the point \((0,0)\) in the coordinate plane. This is where the horizontal axis and the vertical axis cross.
