Lesson 14
Four Representations
14.1: Which is the Bluest? (5 minutes)
Warm-up
In this warm-up, students are asked to reason which group of blocks is the bluest and explain how they arrived at that decision. The goal is to prompt students to visualize and articulate different ways they can use ratios, equivalent ratios and proportions to support their reasoning.
Launch
Students in groups of 2. Tell students you will show them five groups of blocks. Their job is to determine which group of blocks is the bluest. Display the image for all to see. Give students 2 minutes of quiet think time. Encourage students who have one way of supporting their decision to think about another way while they wait.
Student Facing
- Which group of blocks is the bluest?

- Order the groups of blocks from least blue to bluest.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share which group of blocks is the bluest and their reasoning. Record and display student explanations for all to see. To involve more students in the conversation, consider asking some of the following questions:
- Did anyone choose the same group of blocks but would explain it differently?
- Does anyone want to add an observation to the way ____ saw the blocks?
- Do you agree or disagree? Why? Ask students to order the groups of blocks from less blue to bluest after deciding on the bluest group of blocks.
14.2: One Scenario, Four Representations (20 minutes)
Activity
In this activity, students choose from different lists of things to define their own proportional and nonproportional relationships. Some of the things on the list will be familiar and others will be unfamiliar. This is a significant change from previous activities where students were always given two quantities and they had to decide if they were proportional or not. This new step gives students the opportunity to think about what quantities are related to some of the items on the lists, which is an important step of modeling with mathematics (MP4).
This activity and the next go together. Students use the work from this activity to make a visual display of their work in the next activity.
Launch
Arrange students in groups of 2.
The names of things in the task may be unfamiliar to both English Language Learners and fluent English speakers. Before students start, take some time to ensure they know the meaning of their chosen things or ask them to do some research on their meanings. You might ask each pair of students to choose a different unfamiliar word, spend five minutes to research it, and prepare a drawing or explanation to share with the class.
It is best to approve of students’ choices before they work. For example, if students choose “legs” and “earthworms,” that will not make for a very interesting relationship.
Supports accessibility for: Organization; Conceptual processing; Attention
Design Principle(s): Optimize output (for justification); Support sense-making
Student Facing
-
Select two things from different lists. Make up a situation where there is a proportional relationship between quantities that involve these things.
creatures
- starfish
- centipedes
- earthworms
- dinosaurs
length
- centimeters
- cubits
- kilometers
- parsecs
time
- nanoseconds
- minutes
- years
- millennia
volume
- milliliters
- gallons
- bushels
- cubic miles
body parts
- legs
- eyes
- neurons
- digits
area
- square microns
- acres
- hides
- square light-years
weight
- nanograms
- ounces
- deben
- metric tonnes
substance
- helium
- oobleck
- pitch
- glue
- Select two other things from the lists, and make up a situation where there is a relationship between quantities that involve these things, but the relationship is not proportional.
-
Your teacher will give you two copies of the “One Scenario, Four Representations” sheet. For each of your situations, describe the relationships in detail. If you get stuck, consider asking your teacher for a copy of the sample response.
- Write one or more sentences describing the relationship between the things you chose.
- Make a table with titles in each column and at least 6 pairs of numbers relating the two things.
- Graph the situation and label the axes.
- Write an equation showing the relationship and explain in your own words what each number and letter in your equation means.
- Explain how you know whether each relationship is proportional or not proportional. Give as many reasons as you can.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
As students work, pay attention to the numbers they use in their tables. Students can be haphazard when choosing values, and their numbers may end up being unfriendly. You can ask them questions that encourage them to reason about what numbers would be friendlier. Also, depending on the things chosen, they may need to consider scales for their axes. Watch out for scales like {1, 2, 3, . . . } for the number of legs on a centipede!
Creating a relationship that is not proportional may present too significant a challenge for struggling learners. An accommodation would be to change their task to creating only a proportional relationship, or even assigning two quantities that are straightforward like “starfish legs vs. number of starfish.”
Activity Synthesis
Ask groups to trade their work with another group to give feedback about their analysis.
14.3: Make a Poster (15 minutes)
Optional activity
In this activity, students make a visual display of their scenarios from the previous activity (after sharing their rough draft with another group and getting some feedback).
When the posters are complete and displayed around the room, students view each others' work and use sentence starters to give feedback and to critique the reasoning of others (MP3).
Launch
Keep students in the same groups. Tell them that they should incorporate the feedback they received when making their posters.
Supports accessibility for: Attention; Social-emotional skills
Student Facing
Create a visual display of your two situations that includes all the information from the previous activity.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
When the posters are complete, hang them around the room. Provide students with these sentence starters, and give them an opportunity to view their classmates’ work and write their responses. This provides a structured way for students to critique the reasoning of others (MP3).
The most surprising combination of things was ____________________ because ______________________________________________________________.
The group _______________________________ should check their work where they ___________________________________________________________________.
I really liked when the group ____________________________ did this __________________________________ because _______________________________________.
Design Principle(s): Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Reflect on the following questions.
- "Describe any part of your work today that you would do differently, if you could start over."
- "Tell me about something new you learned in this class recently."
- "Tell me about any questions you still have, or anything that is confusing you."
14.4: Cool-down - Explain Their Work (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
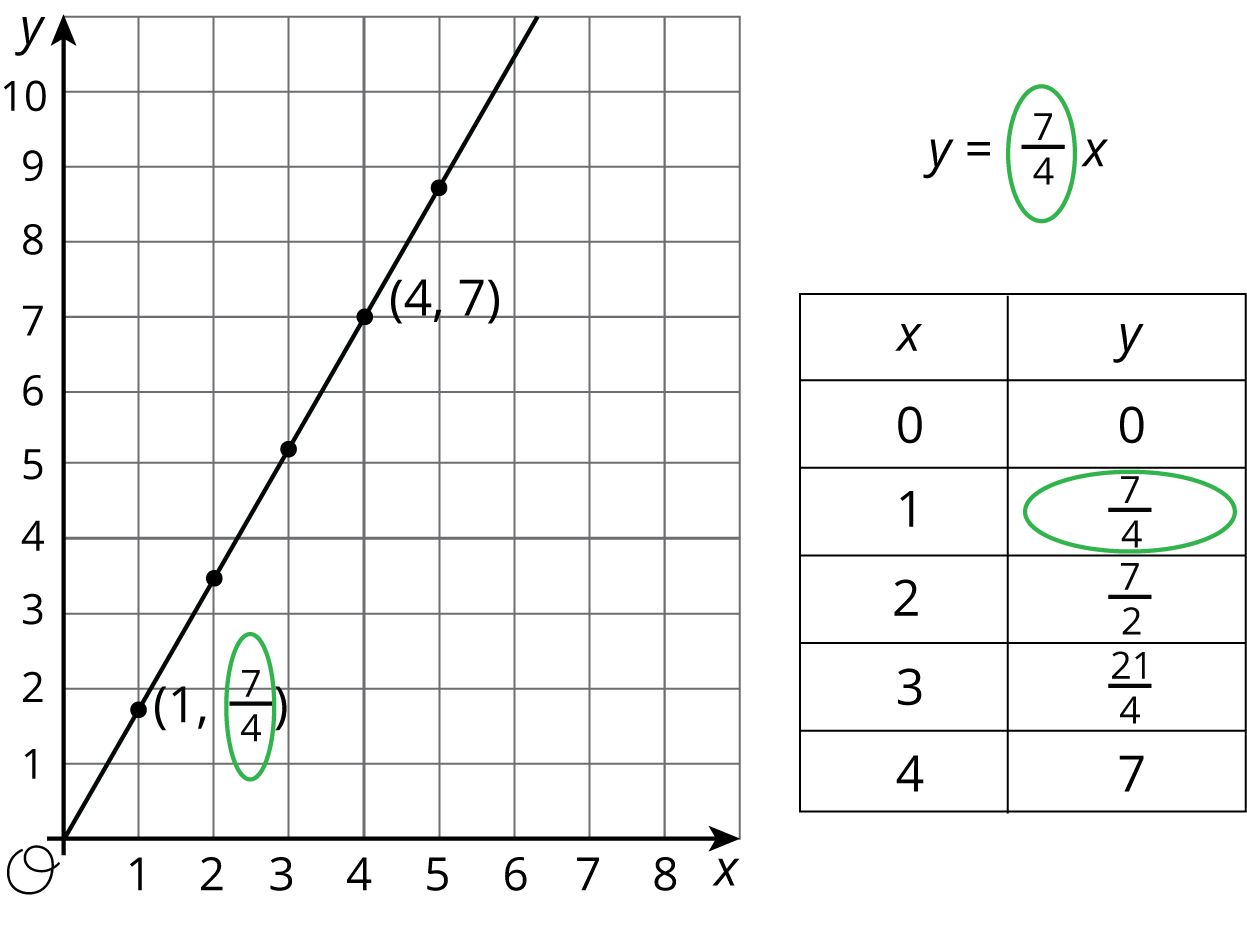
The constant of proportionality for a proportional relationship can often be easily identified in a graph, a table, and an equation that represents it. Here is an example of all three representations for the same relationship. The constant of proportionality is circled:
On the other hand, some relationships are not proportional. If the graph of a relationship is not a straight line through the origin, if the equation cannot be expressed in the form \(y = kx\), or if the table does not have a constant of proportionality that you can multiply by any number in the first column to get the associated number in the second column, then the relationship between the quantities is not a proportional relationship.