Lesson 3
More about Constant of Proportionality
3.1: Equal Measures (5 minutes)
Warm-up
This warm-up prompts students to review work in grade 5 of converting across different-sized standard units within a given measurement system.
Launch
Arrange students in groups of 2. Ask students to use the following numbers and units to record as many equivalent expressions as they can. Tell them they are allowed to reuse numbers and units. Give students 2 minutes of quiet think time followed by 1 minute to share their equations with their partner.
Student Facing
Use the numbers and units from the list to find as many equivalent measurements as you can. For example, you might write “30 minutes is \(\frac12\) hour.”
You can use the numbers and units more than once.
1
12
0.4
60
50
\(\frac{1}{2}\)
40
0.01
\(3\frac{1}{3}\)
30
0.3
24
\(\frac{1}{10}\)
6
2
\(\frac{2}{5}\)
centimeter
meter
hour
feet
minute
inch
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite a few students to share equations that they had in common with their partner and ones that were different. Record these answers for all to see. After each equation is shared, ask students to give a signal if they had the same one recorded. Display the following questions for all to see and discuss:
- “What number(s) did you use the most? Why?”
- “If you could include two more cards to this selection, what would they be? Why?”
3.2: Centimeters and Millimeters (10 minutes)
Activity
This activity has two purposes. First, it involves an important context that can be represented by proportional relationships, namely measurement conversion. Second, it introduces the idea that there are two constants of proportionality, and that they are reciprocals (also known as multiplicative inverses). Students understand why this is the case later when they use equations to represent proportional relationships. Students start to use “is proportional to” language to distinguish between the two constants of proportionality. During the discussion, students should be reminded that dividing by a number is equivalent to multiplying by its reciprocal. In principle, this is something students learn in grade 6, but they often need to be reminded. This will be needed in future lessons, so it is important to discuss it here.
Conversion of centimeters to millimeters has a constant of proportionality of 10 while conversion of millimeters to centimeters has a constant of proportionality of \(\frac{1}{10}\). One way to explain why these two constants of proportionality are multiplicative inverses is to imagine starting with a measurement in centimeters, 15 cm for example. When we convert to millimeters we multiply by 10: 15 cm = 150 mm. If we convert the measurement in millimeters back to centimeters, we know it will be 15, so the constant of proportionality we need to multiply by is \(\frac{1}{10}\).
Launch
Tell students, “Let’s look at how centimeters and millimeters are related and how it is related to what we have been doing recently.”
Supports accessibility for: Memory; Conceptual processing
Student Facing
There is a proportional relationship between any length measured in centimeters and the same length measured in millimeters.

There are two ways of thinking about this proportional relationship.
-
If you know the length of something in centimeters, you can calculate its length in millimeters.
- Complete the table.
- What is the constant of proportionality?
length (cm) length (mm) 9 12.5 50 88.49 -
If you know the length of something in millimeters, you can calculate its length in centimeters.
- Complete the table.
- What is the constant of proportionality?
length (mm) length (cm) 70 245 4 699.1 - How are these two constants of proportionality related to each other?
-
Complete each sentence:
- To convert from centimeters to millimeters, you can multiply by ________.
- To convert from millimeters to centimeters, you can divide by ________ or multiply by ________.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
- How many square millimeters are there in a square centimeter?
- How do you convert square centimeters to square millimeters? How do you convert the other way?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may say that the constants of proportionality are both 10 since you can divide by 10 in the second table. Tell students, “The constant of proportionality is what you multiply by. Can you find a way to multiply the numbers in the first column to get the numbers in second column?”
Activity Synthesis
The goal of this discussion is to help students see the connection between this situation and the earlier tasks, so they can use the structure of the table (MP7) to find the constants of proportionality. Ask questions like, “Can you use any of the strategies we have been discussing in earlier problems to help you solve this problem?” as students work to help them make this connection.
If there is disagreement about the constants of proportionality, ask students to explain their thinking.
Look for students who have seen the connection between dividing by 10 and multiplying by \(\frac{1}{10}\). Ask the students if there is a generalization to be made here. Help them articulate the idea that when you divide by a number, that is the same as multiplying by the reciprocal.
Design Principle(s): Support sense-making
3.3: Pittsburgh to Phoenix (15 minutes)
Activity
This activity focuses on making connections between constant speed and proportional relationships, with special attention to the constant of proportionality. In grade 6, students solved problems involving constant speed, but they need opportunities to make the connection to proportional relationships; students who successfully make this connection are reasoning abstractly about contexts with constant speed (MP2). Students who need support in understanding the context can trace the segments in the map, labeling the distances they know and putting question marks for unknown distances. An empty double number line could also be a useful tool in helping students reason about the context.
The numbers are chosen so that students are more likely to use unit rate rather than scale factors. The goal of the discussion is for students to understand that when speed is constant, time elapsed and distance traveled are proportional. The constant of proportionality indicates the magnitude of the speed. For example, if distance is given in miles and time in hours, then the constant of proportionality indicates the speed in miles per hour.
Students might wonder about the route. If they ask about it, teachers can share some reasons why airplane routes are complex, e.g., the need to avoid congested areas and the fact that the shortest distances on the curved surface of Earth do not always correspond to lines on a map.
Launch
It may have been some time since students reasoned about constant speed, so before they start on this activity, consider posing some simple problems about constant speed. For example:
- Someone walks at a constant speed of 4 miles per hour. How much time does it take them to walk 4 miles? 8 miles? 20 miles? 2 miles? \(\frac12\) mile? How far do they get in 3 hours? In 10 minutes?
- Someone rides a bike at a constant speed. They go 30 miles in 2 hours. What was their speed? If students did some work with double number lines when learning about constant speed in grade 6, they may be inclined to create one to help them think through these launch questions and when they get into the activity. If no one suggests it, it might be worth showing a double number line when talking through this launch, so that while working on the activity, students recall that these are useful tools. For example:

Supports accessibility for: Memory; Conceptual processing
Design Principle(s): Optimize output (for explanation)
Student Facing
On its way from New York to San Diego, a plane flew over Pittsburgh, Saint Louis, Albuquerque, and Phoenix traveling at a constant speed.
Complete the table as you answer the questions. Be prepared to explain your reasoning.
| segment | time | distance | speed |
|---|---|---|---|
| Pittsburgh to Saint Louis | 1 hour | 550 miles | |
| Saint Louis to Albuquerque | 1 hour 42 minutes | ||
| Albuquerque to Phoenix | 330 miles |
-
What is the distance between Saint Louis and Albuquerque?
-
How many minutes did it take to fly between Albuquerque and Phoenix?
- What is the proportional relationship represented by this table?
- Diego says the constant of proportionality is 550. Andre says the constant of proportionality is \(9 \frac16\). Do you agree with either of them? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The goal of the discussion is for students to understand that when speed is constant, then distance traveled is proportional to elapsed time. The constant of proportionality is the speed. For example, if distance is given in miles and time in hours, then the constant of proportionality indicates the speed in miles per hour.
Begin by having a student share a table that is all in hours, miles, and miles per hour. Use this example to point out that every number in the first column can be multiplied by the speed to get the number in the second column. Ask:
- “Which quantities are in a proportional relationship? How do you know?”
- “What is the constant of proportionality in this case?”
If a student wrote their times in minutes and speed in miles per minute, you can have the same discussion if the class seems ready for that leap, but it is not required. In any case, summarize by making it explicit that when time and distance are in a proportional relationship, the constant of proportionality is the speed.
Lesson Synthesis
Lesson Synthesis
Briefly revisit the two contexts, demonstrating the use of new terms. For example,
- In the first activity, we examined the proportional relationship between millimeters and centimeters from two different perspectives and found two constants of proportionality. What were they? What is the relationship between the two constants of proportionality? (They are reciprocals.)
- In the second activity, we examined a proportional relationship between the time a plane flies and the distance it travels. What was the constant of proportionality in this task? What does the constant of proportionality represent in terms of the context? (Magnitude of speed.)
3.4: Cool-down - Fish Tank (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
When something is traveling at a constant speed, there is a proportional relationship between the time it takes and the distance traveled. The table shows the distance traveled and elapsed time for a bug crawling on a sidewalk.
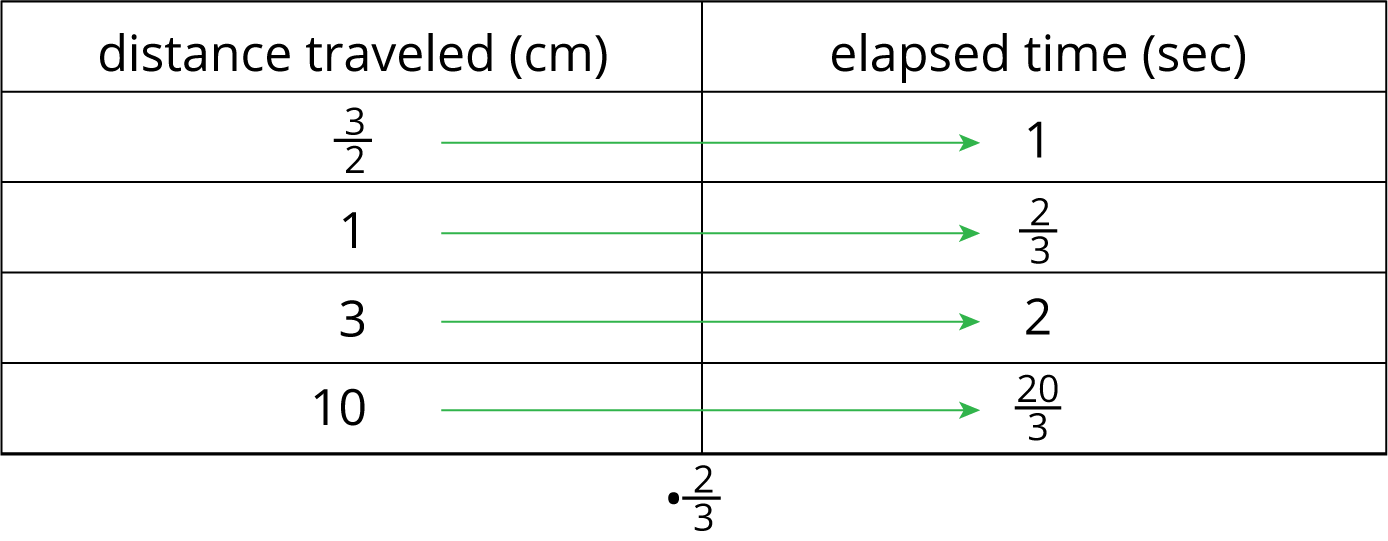
We can multiply any number in the first column by \(\frac23\) to get the corresponding number in the second column. We can say that the elapsed time is proportional to the distance traveled, and the constant of proportionality is \(\frac23\). This means that the bug’s pace is \(\frac23\) seconds per centimeter.
This table represents the same situation, except the columns are switched.
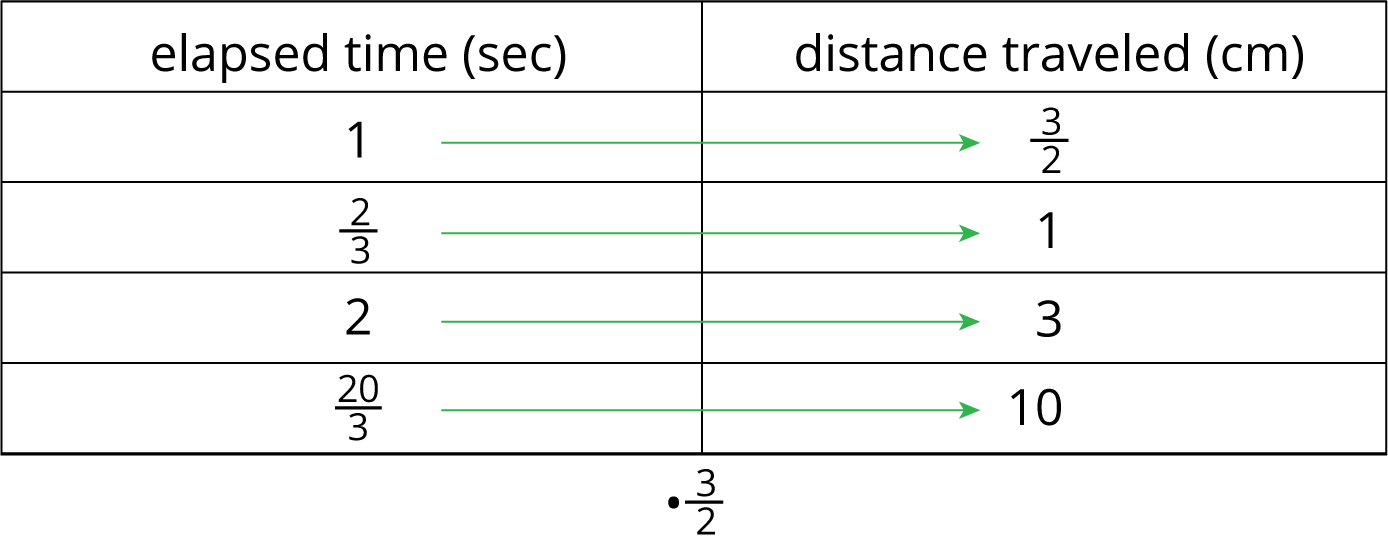
We can multiply any number in the first column by \(\frac32\) to get the corresponding number in the second column. We can say that the distance traveled is proportional to the elapsed time, and the constant of proportionality is \(\frac32\). This means that the bug’s speed is \(\frac32\) centimeters per second.
Notice that \(\frac32\) is the reciprocal of \(\frac23\). When two quantities are in a proportional relationship, there are two constants of proportionality, and they are always reciprocals of each other. When we represent a proportional relationship with a table, we say the quantity in the second column is proportional to the quantity in the first column, and the corresponding constant of proportionality is the number we multiply values in the first column to get the values in the second.