Lesson 13
Two Graphs for Each Relationship
13.1: True or False: Fractions and Decimals (5 minutes)
Warm-up
This warm-up encourages students to connect and reason algebraically about various computational relationships and patterns from previous exercises. While students may evaluate each side of the equation to determine if it is true or false, encourage students to think about the following ideas in each:
- The multiplicative relationships between the factors. Multiplying one factor by 2 and dividing the other by 2 on the left side of the equation results in the two factors on the right hand side.
- In this case, the factors on the left hand side of the equation are adjusted in the same manner as the first equation, however since the operation is division, this strategy results in one side being 4 times the value of the other.
- This equation applies the same reasoning as the first equation except the factors are adjusted by multiplying and dividing by 4.
Launch
Display one problem at a time. Tell students to give a signal when they have an answer and a strategy. After each problem, give students 1 minute of quiet think time and follow with a whole-class discussion.
Student Facing
Decide whether each equation is true or false. Be prepared to explain your reasoning.
- \(\frac32\boldcdot 16 = 3\boldcdot 8\)
- \(\frac34\div\frac12 = \frac64\div\frac14\)
- \((2.8)\boldcdot (13) = (0.7)\boldcdot (52)\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may think the same strategies that work for multiplication can be applied to division. For these students ask them for a context to demonstrate what happens we we double a dividend and halve the divisor.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their explanations for all to see. Ask students if or how the factors in the problem impacted the strategy choice. To involve more students in the conversation, consider asking:
- “Do you agree or disagree? Why?”
- “Who can restate ___’s reasoning in a different way?”
- “Does anyone want to add on to _____’s strategy?”
- “Will that strategy always work? How do you know?”
After each true equation, ask students if they could rely on the same reasoning to determine if other similar problems are equivalent. After each false equation, ask students how the problem could be changed to make the equation true.
13.2: Tables, Graphs, and Equations (20 minutes)
Activity
Note: if it is possible in your local environment, we recommend using the digital version of this activity.
This activity is intended to help students identify correspondences between parts of a table, graph, and an equation of a line through the origin in the first quadrant. Students are guided to notice:
- Any pair of positive values \((a, b)\) determine a proportional relationship.
- Given a point \((a,b)\) other than the origin on the graph of a line through the origin, the constant of proportionality is always \(\frac{b}{a}\).
- In an equation \(y=\frac{b}{a} x\) that represents the relationship, the constant of proportionality appears as the coefficient of \(x\).
- The constant of proportionality is the \(y\)-coordinate when \(x\) is 1, that is, \((1,\frac{b}{a})\) is a point on the graph.
In the print version, students plot one point and draw a ray that starts at the origin and passes through their point. They also create a table and an equation to represent the relationship. They respond to a series of questions about their representations. Then, they compare their representations of their relationship with the representations of other relationships created by members of their group.
In the digital version (recommended), students interact with a dynamic sketch while recording observations and responding to prompts. In the sketch, students are able to manipulate the graph of a proportional relationship, while changes to an associated table and equation automatically update.
Launch
For the print version: Arrange students in groups of 3. Assign each student in each group a letter: A, B, or C. Provide access to rulers.
For the digital version: Arrange students in groups of 2–3 and have them complete the task.
Supports accessibility for: Organization; Attention
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
Explore the graph. Start by dragging the gray bar on the left across the screen until you can see both the table and the graph. Notice the values in the table and the coordinates of the labeled point. Grab the point and move it around.
- What stays the same and what changes in the table? in the equation? on the graph?
- Choose one row in the table and write it here. To what does this row correspond on the graph?
| \(x\) | \(y\) |
|---|---|
Grab and drag the point until you see the equation \(y=\frac 32 x\).
- Do not move the point. Choose three rows from the table, other than the origin. Record \(x\) and \(y\), and compute \(\frac yx\).
| \(x\) | \(y\) | \(\frac{y}{x}\) |
|---|---|---|
- What do you notice? What does this have to do with the equation of the line?
- Do not move the point. Check the box to view the coordinates \((1, ?)\). What are the coordinates of this point? What does this correspond to in the table? What does this correspond to in the equation?
- Drag the point to a different location. Record the equation of the line, the coordinates of three points, and the value of \(\frac yx\).
Equation of the line: _______________________________
| \(x\) | \(y\) | \(\frac{y}{x}\) |
|---|---|---|
- Based on your observations, summarize any connections you see between the table, characteristics of the graph, and the equation.
Student Response
For access, consult one of our IM Certified Partners.
Launch
For the print version: Arrange students in groups of 3. Assign each student in each group a letter: A, B, or C. Provide access to rulers.
For the digital version: Arrange students in groups of 2–3 and have them complete the task.
Supports accessibility for: Organization; Attention
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
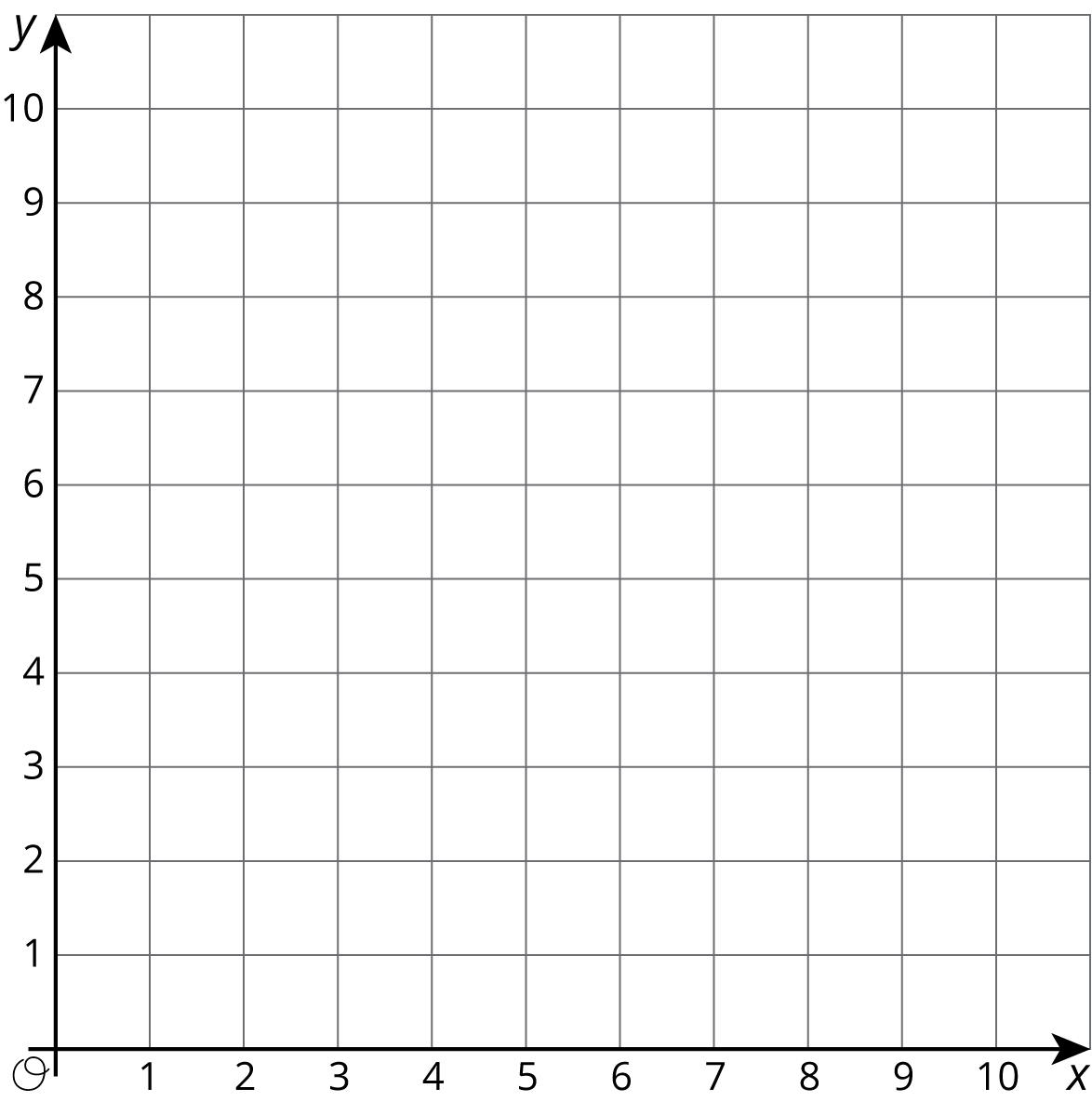
Your teacher will assign you one of these three points:
\(A=(10,4)\), \(B=(4,5)\), \(C=(8,5)\).
| \(x\) | \(y\) | \(\frac{y}{x}\) |
|---|---|---|
| 0 | NA | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 |
- On the graph, plot and label only your assigned point.
- Use a ruler to line up your point with the origin, \((0,0)\). Draw a line that starts at the origin, goes through your point, and continues to the edge of the graph.
- Complete the table with the coordinates of points on your graph. Use a fraction to represent any value that is not a whole number.
- Write an equation that represents the relationship between \(x\) and \(y\) defined by your point.
-
Compare your graph and table with the rest of your group. What is the same and what is different about:
- your tables?
- your equations?
- your graphs?
- What is the \(y\)-coordinate of your graph when the \(x\)-coordinate is 1? Plot and label this point on your graph. Where do you see this value in the table? Where do you see this value in your equation?
- Describe any connections you see between the table, characteristics of the graph, and the equation.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
The graph of an equation of the form \(y = kx\), where \(k\) is a positive number, is a line through \((0,0)\) and the point \((1,k)\).
- Name at least one line through \((0,0)\) that cannot be represented by an equation like this.
- If you could draw the graphs of all of the equations of this form in the same coordinate plane, what would it look like?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
When all students have completed the activity, ask them to share their responses with a partner or small group. After a minute, go around the room asking each group to share one thing from the last question, and display these for all to see. When each group has shared, ask if there were any important observations that were missed.
Ensure that all the important connections are highlighted:
- A graph of a line through the origin and passing through the first quadrant represents a proportional relationship.
- The value of \(\frac ba\) computed from any point \((a,b)\) on that line (other than the origin) is the constant of proportionality.
- An equation of the relationship is given by \(y = kx\) where \(k\) is \(\frac ba\) for any point \((a,b)\) on the graph other than the origin.
13.3: Hot Dog Eating Contest (10 minutes)
Activity
The purpose of this activity is to help students understand derived units and rates. It is intended to help students see that a proportional relationship between two quantities is associated with two rates. The first rate indicates how many hot dogs someone eats in one minute (number of hot dogs per minute), and the second indicates how many minutes it takes to eat one hot dog (number of minutes per hot dog). The need for care with units (MP6) will become very clear should any students express rates in seconds per hot dog. If any students make this choice, it can be an opportunity to make connections between different ways of representing the same situation.
Monitor for students who take each approach.
Launch
Keep students in the same groups.
Supports accessibility for: Visual-spatial processing
Student Facing
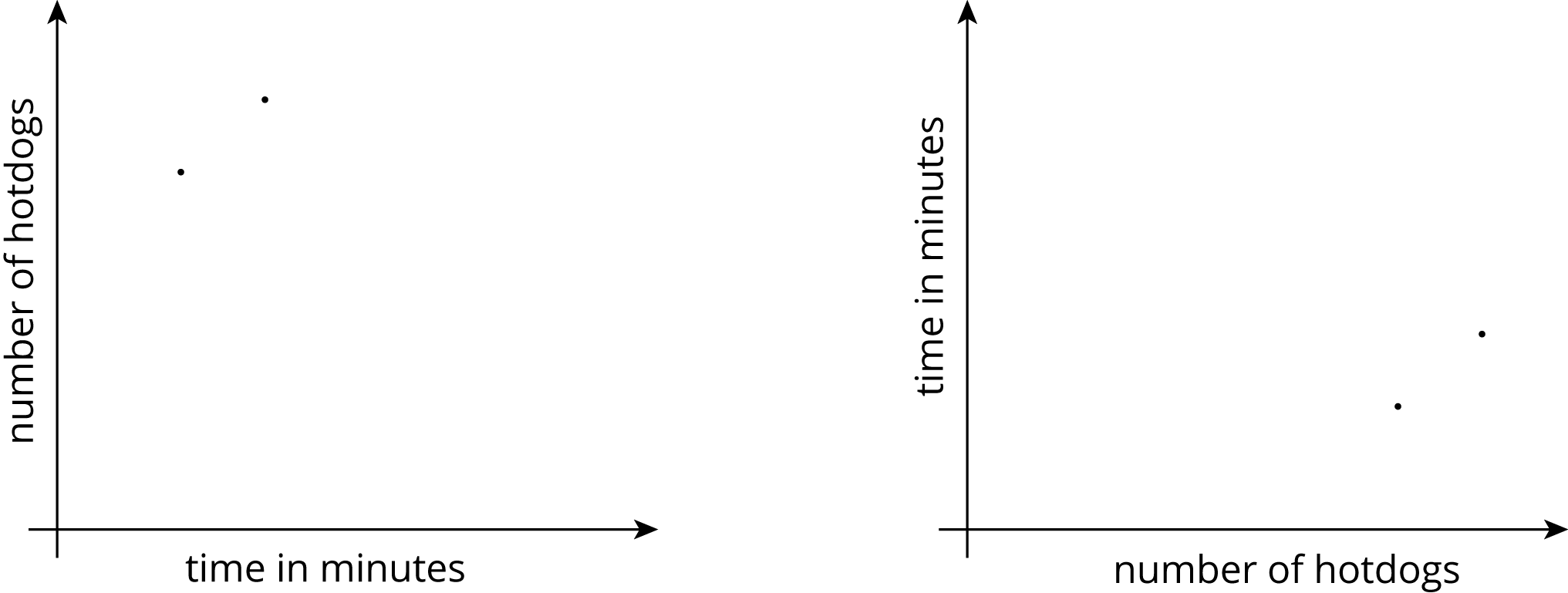
Andre and Jada were in a hot dog eating contest. Andre ate 10 hot dogs in 3 minutes. Jada ate 12 hot dogs in 5 minutes.
-
The points shown on the first set of axes display information about Andre’s and Jada’s consumption. Which point indicates Andre’s consumption? Which indicates Jada’s consumption? Label them.
-
Draw two lines: one through the origin and Andre’s point, and one through the origin and Jada’s point. Write an equation for each line. Use \(t\) to represent time in minutes, and \(h\) to represent number of hot dogs.
-
For each equation, what does the constant of proportionality tell you?
-
The points shown on the second set of axes display information about Andre’s and Jada’s consumption. Which point indicates Andre’s consumption? Which indicates Jada’s consumption? Label them.
-
Draw lines from the origin through each of the two points. Write an equation for each line. What does the constant of proportionality tell you in each case?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Keep students in the same groups.
Supports accessibility for: Visual-spatial processing
Student Facing
Andre and Jada were in a hot dog eating contest. Andre ate 10 hot dogs in 3 minutes. Jada ate 12 hot dogs in 5 minutes.
Here are two different graphs that both represent this situation.
-
On the first graph, which point shows Andre’s consumption and which shows Jada’s consumption? Label them.
-
Draw two lines: one through the origin and Andre’s point, and one through the origin and Jada’s point.
-
Write an equation for each line. Use \(t\) to represent time in minutes and \(h\) to represent number of hot dogs.
-
Andre:
-
Jada:
-
-
For each equation, what does the constant of proportionality tell you?
-
Repeat the previous steps for the second graph.
-
Andre:
-
Jada:
-
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select students to share their reasoning. An important point to bring out in the discussion is that we can describe the rate of hot dog eating in two different ways as hot dogs per minute or minutes per hot dog.
Consider asking the following sequence of questions:
- “At what rate did Andre eat hot dogs?” (Some students might say \(\frac{10}{3}\) or three and a third, while some say \(\frac{3}{10}\) or 0.3.)
- “Well, you’re both right, but we need more information to know what you’re talking about. Can you be more precise?” (This will prompt students to modify their response and say “\(\frac{10}{3}\) or three and a third hot dogs per minute” and “\(\frac{3}{10}\) or 0.3 minutes per hot dog.”)
Reassure students that either response is correct, as long as units are included. The important thing is that we communicate the meaning of the number clearly. Highlight the fact that \(\frac{3}{10}\) and \(\frac{10}{3}\) are reciprocals of each other.
Lesson Synthesis
Lesson Synthesis
Display the graphs and the corresponding equations from the "Hot Dog Eating Contest" activity. Ask student:
- "Do the graphs and equations tell the same story?"
- "How can you see the same information in both?"
When we have two quantities \(x\) and \(y\) in a proportional relationship, we have two choice for writing an equation, making a table, and drawing a graph to represent the relationship. Often the choice is arbitrary and if two people have made different choices, i.e. one views \(x\) as proportional to \(y\) and the other views \(y\) as proportional to \(x\), the representations are related and still provide the same information.
Recall the new units used for the constants of proportionality in the activity: hot dogs per minute, minutes per hot dog. Note that if there is a proportional relationship between two quantities with units \(A\) and \(B\), then the associated rates are expressed in \(A\)s per \(B\) and \(B\)s per \(A\).
13.4: Cool-down - Spicy Popcorn (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Imagine that a faucet is leaking at a constant rate and that every 2 minutes, 10 milliliters of water leaks from the faucet. There is a proportional relationship between the volume of water and elapsed time.
- We could say that the elapsed time is proportional to the volume of water. The corresponding constant of proportionality tells us that the faucet is leaking at a rate of \(\frac15\) of a minute per milliliter.
- We could say that the volume of water is proportional to the elapsed time. The corresponding constant of proportionality tells us that the faucet is leaking at a rate of 5 milliliters per minute.
Let’s use \(v\) to represent volume in milliliters and \(t\) to represent time in minutes. Here are graphs and equations that represent both ways of thinking about this relationship:
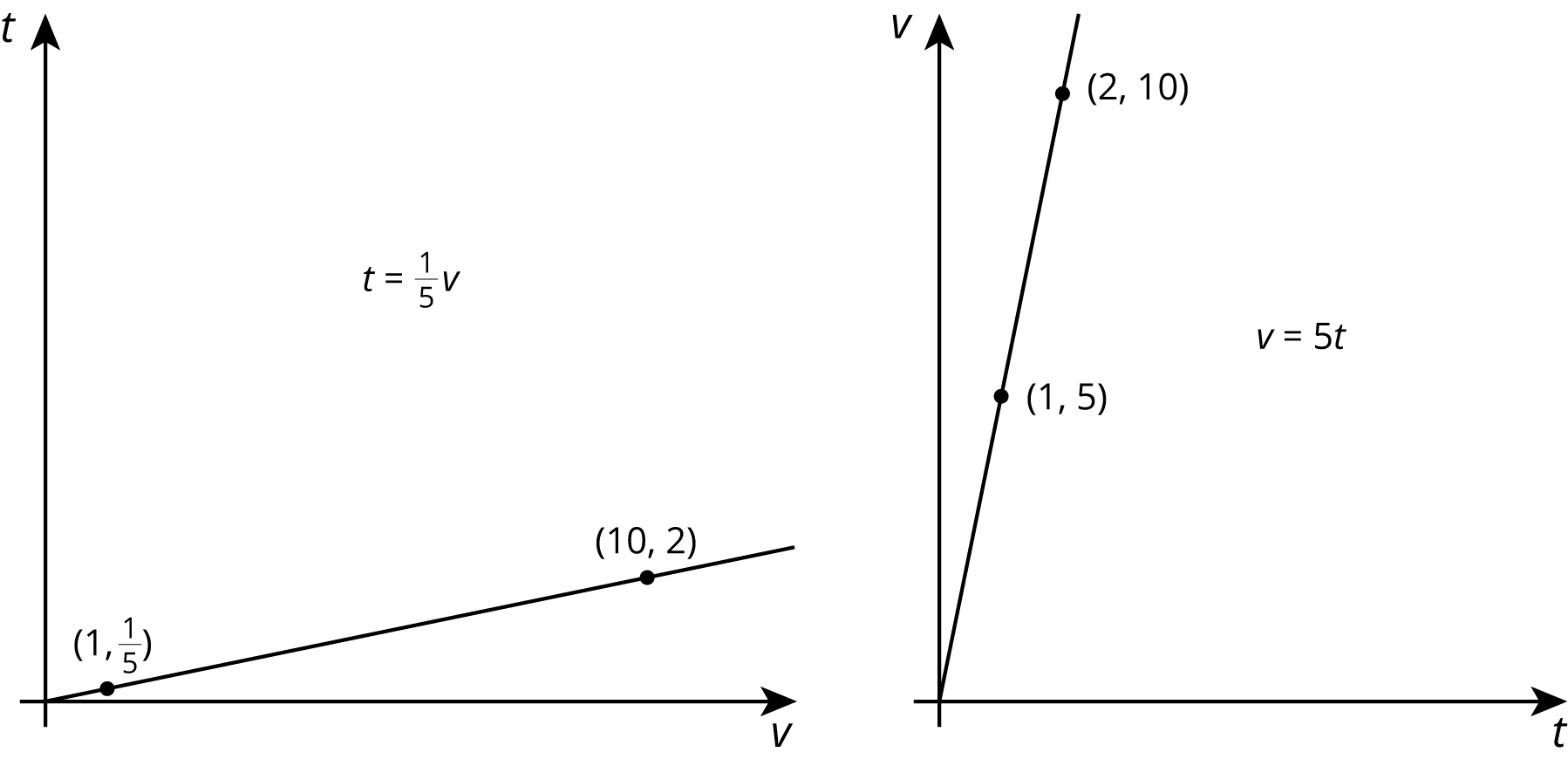
Even though the relationship between time and volume is the same, we are making a different choice in each case about which variable to view as the independent variable. The graph on the left has \(v\) as the independent variable, and the graph on the right has \(t\) as the independent variable.