Lesson 1
One of These Things Is Not Like the Others
1.1: Remembering Double Number Lines (5 minutes)
Warm-up
This activity prompts students to reason about equivalent ratios on a double number line and think of reasonable scenarios for these ratios as a review of their work in grade 6. As students discuss their answers with their partner, select students to share their answers during the whole-class discussion.
Launch
Arrange students in groups of 2. Display the double number line for all to see. Give students 2 minutes of quiet think time and ask them to give a signal when they have found the missing values. Ask students to compare their double number line with a partner and share the values they placed on the number line and their reasoning for each.
Student Facing
-
Complete the double number line diagram with the missing numbers.

- What could each of the number lines represent? Invent a situation and label the diagram.
- Make sure your labels include appropriate units of measure.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may struggle thinking of a scenario with a \(1:2\) ratio. For those students, ask them if they can draw a picture that would represent that ratio and label each line accordingly.
Activity Synthesis
Invite selected students to explain how they reasoned about possible labels for each of the number lines and the units of each. After each student shares, invite others to agree, disagree, or question the reasonableness of the number line descriptions. If there is time, ask students to name other equivalent ratios that would appear if the double number line continued to the right.
1.2: Mystery Mixtures (15 minutes)
Activity
The purpose of this activity is for students to articulate that the taste of the mixture depends both on the amount of water and the amount of drink mix used to make the mixture.
Ideally, students come into the class knowing how to draw and use diagrams or tables of equivalent ratios to analyze contexts like the one in the task. If the diagnostic assessment suggests that some students can and some students can’t, make strategic pairings of students for this task.
Launch
Show students images of the drinks.




If possible, give each student three cups containing the drink mixtures.
Tell students to work through the first question and pause for a discussion. Ask questions like,
- “What does it mean to say that it has more drink mix in it?”
- “Imagine you take different amounts of the two that taste the same. There will be more drink mix in the larger amount, but it will not taste different. Why is that?”
The goal is to see that in the same quantity of each mixture (say a teaspoon), the more flavored drink mixture has more drink mix for the same amount of water. (Alternatively, we can say the more flavored drink mixture has less water for the same amount of drink mix.) Use MLR 8 (Discussion Supports) by making gestures or acting out facial expressions for “strength” of the mixture.
After the students have made some progress understanding this idea, the class should continue to the second question. If students finish quickly, press them to find the amount of drink mix per cup of water in each recipe, thus emphasizing the unit rate.
Design Principle(s): Support sense-making
Student Facing
Your teacher will show you three mixtures. Two taste the same, and one is different.
- Which mixture tastes different? Describe how it is different.
-
Here are the recipes that were used to make the three mixtures:
- 1 cup of water with \(1\frac12\) teaspoons of powdered drink mix
- 2 cups of water with \(\frac12\) teaspoon of powdered drink mix
- 1 cup of water with \(\frac14\) teaspoon of powdered drink mix
Which of these recipes is for the stronger tasting mixture? Explain how you know.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Salt and sugar give two distinctly different tastes, one salty and the other sweet. In a mixture of salt and sugar, it is possible for the mixture to be salty, sweet or both. Will any of these mixtures taste exactly the same?
- Mixture A: 2 cups water, 4 teaspoons salt, 0.25 cup sugar
- Mixture B: 1.5 cups water, 3 teaspoons salt, 0.2 cup sugar
- Mixture C: 1 cup water, 2 teaspoons salt, 0.125 cup sugar
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The key takeaway from this activity is that the flavor depends on both how much drink mix and how much water there is in the mixture. For a given amount of water, the more drink mix you add, the stronger the mixture tastes. Likewise, for a given amount of drink mix, the more water you add, the weaker the mixture tastes. To compare the amount of flavor of two mixtures, when both the amounts of drink mix and the amounts of water are different in the two mixtures, we can write ratios equivalent to each situation so that we are comparing the amount of drink mix for the same amount of water or the amount of water for the same amount of drink mix. Computing a unit rate for each situation is a particular instance of this strategy. Make these ideas explicit if the students do not express them.
If students do not create them, draw discrete diagrams like this:

Or double number line diagrams like this:

For each mixture, identify correspondences between the discrete and number line diagrams, and between the diagrams and tables:
| water (cups) | drink mix (teaspoons) |
|---|---|
| 1 | \(1\frac12\) |
| 2 | 3 |
| water (cups) | drink mix (teaspoons) |
|---|---|
| 2 | \(\frac12\) |
| 1 | \(\frac14\) |
Ask questions like, “On the double number line diagram we see the 1 to \(1\frac12\) relationship at the first tick mark. Where do we see that relationship in the double tape diagram? In the table?”
Use MLR 7 (Compare and Connect) for students to compare methods of how they knew which recipe was strongest. Who used multiplication? Who used division? Who used a unit rate of water per drink mix teaspoon? Who used a unit rate of drink mix per water cup?
Supports accessibility for: Visual-spatial processing
1.3: Crescent Moons (15 minutes)
Activity
In the previous unit, students studied scale drawings of real-world objects. In grade 8, they will study dilations and similarity. The purpose of this activity is to use students’ recent study of scale drawings as a transition to the study of proportional relationships. Initially, students may describe the difference between Moons A, B, C, and D in qualitative terms, e.g., “D is more squished than the others.” They may also use the term “scaled copies,” which appeared in the work of the previous unit, but struggle to identify measurements to use in these figures that consist only of curved sides. It is important to ask students to articulate what they mean by “squished” in quantitative terms, for example, by talking about the height relative to the width and helping students to define “height” and “width” of a moon in some appropriate way. Once students have that, they can note that the height of the enclosing rectangle is always one and a half times its width for Moons A, B, and C, but not D, or they might note that the distance tip to tip is three times the width of the widest part of the moon for Moons A, B, and C, but not so for D.
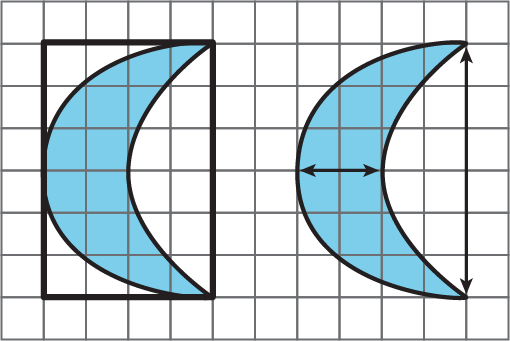
As students explore these transformations, ask questions with the goal of having students articulate that for two images to look like scaled copies of each other, the ratios of the side lengths need to be the same.
In the third question, students are asked to represent the situation with tables and double number line diagrams, providing students with an opportunity to recall these representations from their work in grade 6.
Launch
Give students 3 minutes of quiet think time and tell them to pause after the first two questions. After the quiet think time, ask students to discuss their answers with a partner to describe how Moon D is different. Use MLR 2 (Collect and Display) as students share. Record the explanations that students are using to describe the moons. Ensure that students see some ways to measure lengths associated with the moons, then complete the last question.
If using the digital activity, give students 3 minutes of quiet think time and tell them to pause after the first two questions. After the quiet think time, students can discuss answers with a partner. Based on student conversations, you may want to have a whole-group discussion to ensure they see a way to measure the lengths associated with the moons before they attempt to answer the last question.
Supports accessibility for: Memory; Organization
Student Facing
Here are four different crescent moon shapes.
- What do Moons A, B, and C all have in common that Moon D doesn’t?
- Use numbers to describe how Moons A, B, and C are different from Moon D.
- Use a table or a double number line to show how Moons A, B, and C are different from Moon D.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Can you make one moon cover another by changing its size? What does that tell you about its dimensions?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Give students 3 minutes of quiet think time and tell them to pause after the first two questions. After the quiet think time, ask students to discuss their answers with a partner to describe how Moon D is different. Use MLR 2 (Collect and Display) as students share. Record the explanations that students are using to describe the moons. Ensure that students see some ways to measure lengths associated with the moons, then complete the last question.
If using the digital activity, give students 3 minutes of quiet think time and tell them to pause after the first two questions. After the quiet think time, students can discuss answers with a partner. Based on student conversations, you may want to have a whole-group discussion to ensure they see a way to measure the lengths associated with the moons before they attempt to answer the last question.
Supports accessibility for: Memory; Organization
Student Facing
Here are four different crescent moon shapes.

- What do Moons A, B, and C all have in common that Moon D doesn’t?
- Use numbers to describe how Moons A, B, and C are different from Moon D.
- Use a table or a double number line to show how Moons A, B, and C are different from Moon D.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
For question 2, students might attempt to find the area of each moon by counting individual square units. Suggest that they create a rectangle around each moon instead and compare the width-height ratios.
For question 3, if students are not sure how to set up these representations, providing a template may be helpful.
Activity Synthesis
As students suggest ways to characterize the difference between Moons A, B, and C and Moon D, ask questions that help them clarify and make their statements more precise. For example,
- “What does it mean to be ‘smashed down?’ What measurements might you make to show that this is true?”
- “Is there anything else about what A, B, and C have in common that you can identify?”
- “What things might we measure about these moons to be able to talk about what makes them different in a more precise way?”
- “How can you represent the ratios of the measurements you are comparing using a table and a double number line diagram?”
If some students are still struggling with the tables or diagrams, ask students who were successful to share their representations with the class.
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
Revisit each activity (the drink mixture and the moons), and note that in each, there are two quantities. The ratios of those quantities are equivalent for all but one of the things, the one that is different in an important way. This unit is the study of situations where equivalent ratios characterize something important about a situation. As part of the discussion, use and emphasize ratio and rate language in contexts and review representations like double number line diagrams and tables of equivalent ratios.
- “In what important way were the drink mixtures the same and different?”
- “How could we tell using ratios that these were the same and different?”
- “In what important way were the moons the same and different?”
- “How could we tell using numbers that these were the same and different?”
1.4: Cool-down - Orangey-Pineapple Juice (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
When two different situations can be described by equivalent ratios, that means they are alike in some important way.
An example is a recipe. If two people make something to eat or drink, the taste will only be the same as long as the ratios of the ingredients are equivalent. For example, all of the mixtures of water and drink mix in this table taste the same, because the ratios of cups of water to scoops of drink mix are all equivalent ratios.
| water (cups) | drink mix (scoops) |
|---|---|
| 3 | 1 |
| 12 | 4 |
| 1.5 | 0.5 |
If a mixture were not equivalent to these, for example, if the ratio of cups of water to scoops of drink mix were \(6:4\), then the mixture would taste different.
Notice that the ratios of pairs of corresponding side lengths are equivalent in figures A, B, and C. For example, the ratios of the length of the top side to the length of the left side for figures A, B, and C are equivalent ratios. Figures A, B, and C are scaled copies of each other; this is the important way in which they are alike.

If a figure has corresponding sides that are not in a ratio equivalent to these, like figure D, then it’s not a scaled copy. In this unit, you will study relationships like these that can be described by a set of equivalent ratios.