Lesson 4
Adding and Subtracting Decimals with Many Non-Zero Digits
Let’s practice adding and subtracting decimals.
4.1: The Cost of a Photo Print
-
Here are three ways to write a subtraction calculation. What do you notice? What do you wonder?
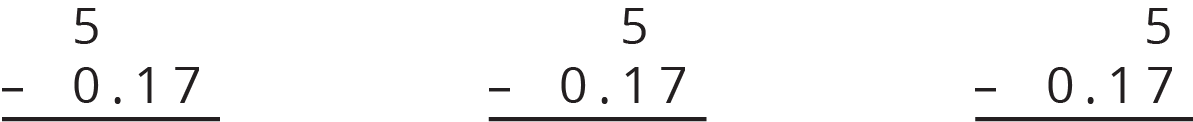
-
Clare bought a photo for 17 cents and paid with a $5 bill. Look at the previous question. Which way of writing the numbers could Clare use to find the change she should receive? Be prepared to explain how you know.
-
Find the amount of change that Clare should receive. Show your reasoning, and be prepared to explain how you calculate the difference of 0.17 and 5.
4.2: Decimals All Around
-
Find the value of each expression. Show your reasoning.
- \(11.3 - 9.5\)
- \(318.8 - 94.63\)
- \(0.02 - 0.0116\)
-
Discuss with a partner:
- Which method or methods did you use in the previous question? Why?
- In what ways were your methods effective? Was there an expression for which your methods did not work as well as expected?
- Lin’s grandmother ordered needles that were 0.3125 inches long to administer her medication, but the pharmacist sent her needles that were 0.6875 inches long. How much longer were these needles than the ones she ordered? Show your reasoning.
- There is 0.162 liter of water in a 1-liter bottle. How much more water should be put in the bottle so it contains exactly 1 liter? Show your reasoning.
- One micrometer is 1 millionth of a meter. A red blood cell is about 7.5 micrometers in diameter. A coarse grain of sand is about 70 micrometers in diameter. Find the difference between the two diameters in meters. Show your reasoning.
4.3: Missing Numbers
Write the missing digits in each calculation so that the value of each sum or difference is correct. Be prepared to explain your reasoning.
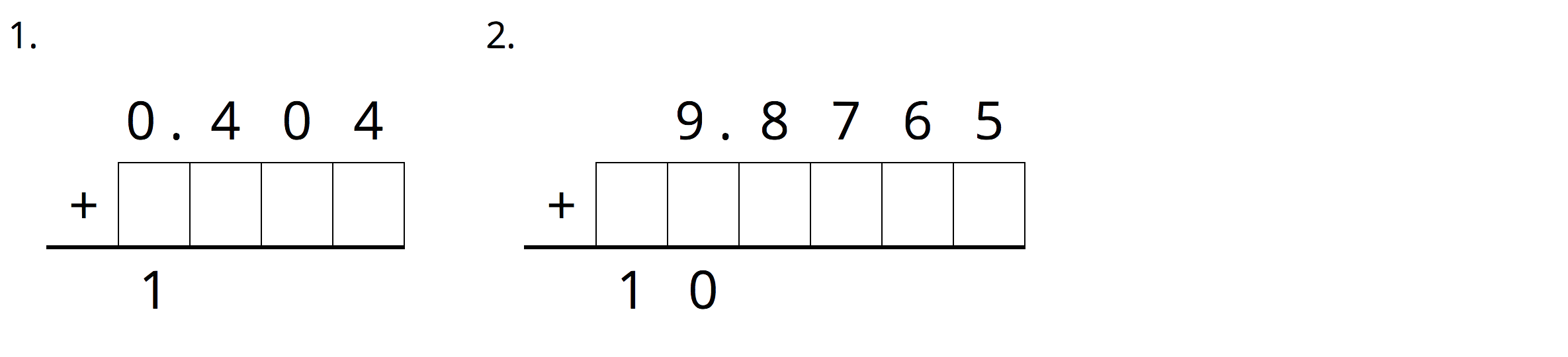
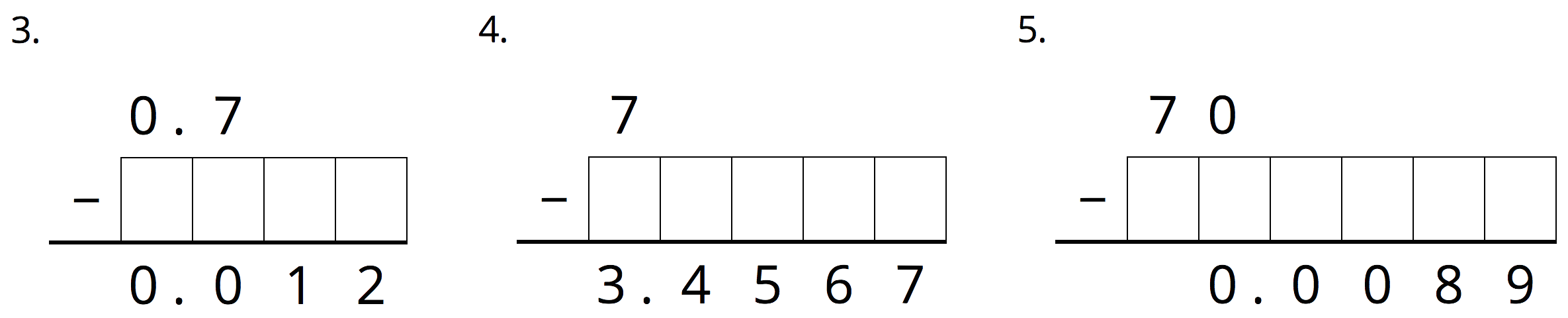
In a cryptarithmetic puzzle, the digits 0-9 are represented using the first 10 letters of the alphabet. Use your understanding of decimal addition to determine which digits go with the letters A, B, C, D, E, F, G, H, I, and J. How many possibilities can you find?
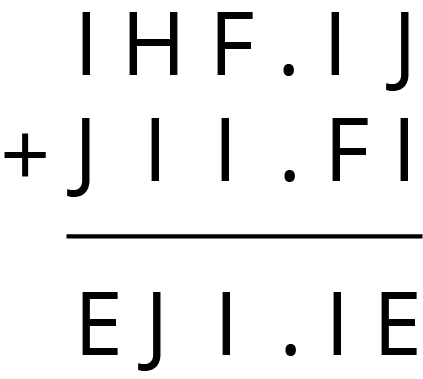
Summary
Base-ten diagrams work best for representing subtraction of numbers with few non-zero digits, such as \(0.16 - 0.09\). For numbers with many non-zero digits, such as \(0.25103 - 0.04671\), it would take a long time to draw the base-ten diagram. With vertical calculations, we can find this difference efficiently.
Thinking about base-ten diagrams can help us make sense of this calculation.
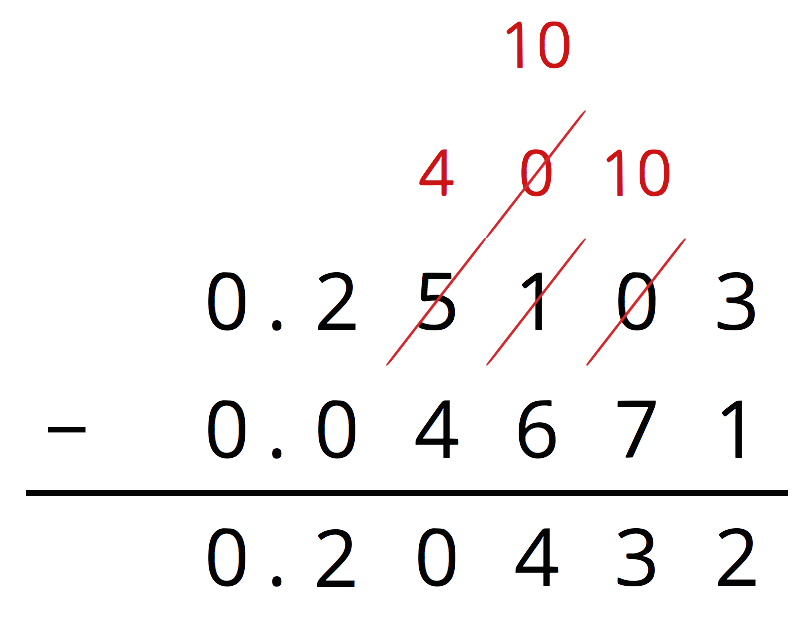
The thousandth in 0.25103 is unbundled (or decomposed) to make 10 ten-thousandths so that we can subtract 7 ten-thousandths. Similarly, one of the hundredths in 0.25103 is unbundled (or decomposed) to make 10 thousandths.