Lesson 11

Dividing Numbers that Result in Decimals

View Student Lesson

Problem 1

Use long division to show that the fraction and decimal in each pair are equal.

\(\frac{3}{4}\) and 0.75

\(\frac{3}{50}\) and 0.06

\(\frac{7}{25}\) and 0.28

 

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Mai walked \(\frac{1}{8}\) of a 30-mile walking trail. How many miles did Mai walk? Explain or show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Use long division to find each quotient. Write your answer as a decimal.

  1. \(99\div 12\)

  2. \(216 \div 5\)

  3. \(1,\!988 \div 8\)

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Tyler reasoned: “\(\frac{9}{25}\) is equivalent to \(\frac{18}{50}\) and to \(\frac {36}{100}\), so the decimal of \(\frac{9}{25}\) is 0.36.”
 

  1. Use long division to show that Tyler is correct.

  2. Is the decimal of \(\frac{18}{50}\) also 0.36? Use long division to support your answer.

Solution

For access, consult one of our IM Certified Partners.

Problem 5

Complete the calculations so that each shows the correct difference.

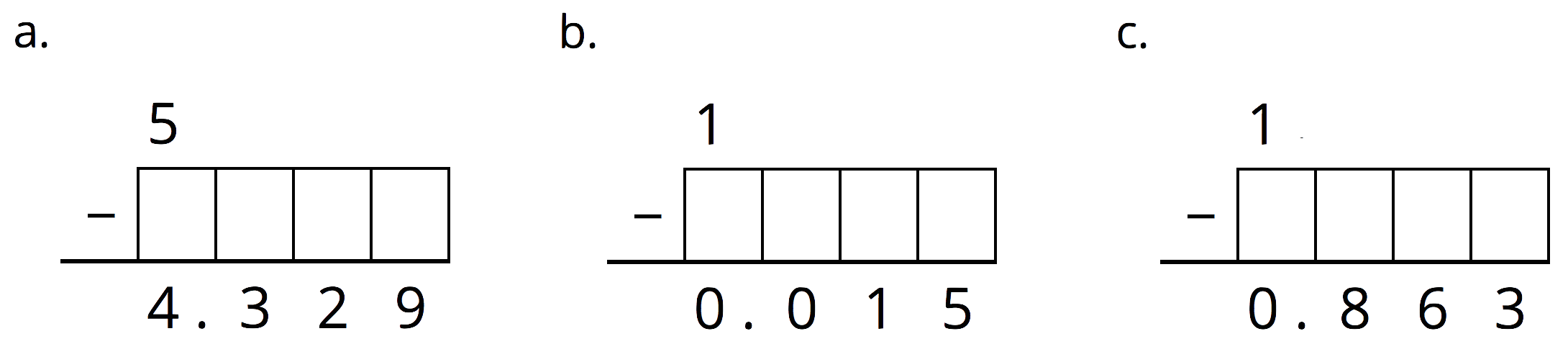
3 fill in the blank subtraction problems.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 5, Lesson 4.)

Problem 6

Use the equation \(124 \boldcdot 15 = 1,\!860\) and what you know about fractions, decimals, and place value to explain how to place the decimal point when you compute \((1.24) \boldcdot (0.15)\).

Solution

For access, consult one of our IM Certified Partners.

(From Unit 5, Lesson 6.)