Lesson 15
Part-Part-Whole Ratios
Lesson Narrative
Up to this point, students have worked with ratios of quantities where the units are the same (e.g., cups to cups) and ratios of quantities where the units are different (e.g., miles to hours). Sometimes in the first case, the sum of the quantities makes sense in the context, and we can ask questions about the total amount as well as the component parts. For example, when mixing 3 cups of yellow paint with 2 cups of blue paint, we get a total of 5 cups of green paint. (Notice that this does not always work; 3 cups of water mixed with 2 cups of dry oatmeal will not make 5 cups of soggy oatmeal.) In the paint scenario, the ratio of yellow paint to blue paint to green paint is \(3 : 2 : 5\). Furthermore, if we double the amount of both yellow and blue paint, we will double the amount of green paint. In general, if the ratio of yellow to blue paint is equivalent, the ratio of yellow to blue to green paint will also be the equivalent. We can see this is always true because of the distributive property:
\(a : b : (a+b)\) is equivalent to \(2a : 2b : (2a+2b)\) because \(2a+2b = 2(a+b)\).
These ratios are sometimes called “part-part-whole” ratios.
In this lesson, students learn about tape diagrams as a handy tool to represent ratios with the same units and as a way to reason about individual quantities (the parts) and the total quantity (the whole). Here students also see ratios expressed not in terms of specific units (milliliters, cups, square feet, etc.) but in terms of “parts” (e.g., the recipe calls for 2 parts of glue to 1 part of water).
Learning Goals
Teacher Facing
- Comprehend the word “parts” as an unspecified unit in sentences (written and spoken) describing ratios.
- Draw and label a tape diagram to solve problems involving ratios and the total amount. Explain (orally) the solution method.
Student Facing
Let’s look at situations where you can add the quantities in a ratio together.
Required Materials
Required Preparation
Prepare a set of 50 red snap cubes and 30 blue snap cubes for each group of students.
Learning Targets
Student Facing
- I can create tape diagrams to help me reason about problems involving a ratio and a total amount.
- I can solve problems when I know a ratio and a total amount.
Glossary Entries
-
tape diagram
A tape diagram is a group of rectangles put together to represent a relationship between quantities.
For example, this tape diagram shows a ratio of 30 gallons of yellow paint to 50 gallons of blue paint.
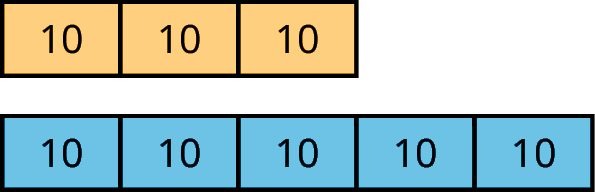
If each rectangle were labeled 5, instead of 10, then the same picture could represent the equivalent ratio of 15 gallons of yellow paint to 25 gallons of blue paint.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |