Lesson 13
Tables and Double Number Line Diagrams
Problem 1
The double number line shows how much water and how much lemonade powder to mix to make different amounts of lemonade.

Make a table that represents the same situation.
Solution
For access, consult one of our IM Certified Partners.
Problem 2
A bread recipe uses 3 tablespoons of olive oil for every 2 cloves of crushed garlic.
- Complete the table to show different-sized batches of bread that taste the same as the recipe.
- Draw a double number line that represents the same situation.
- Which representation do you think works better in this situation? Explain why.
| olive oil (tablespoons) | crushed garlic (cloves) |
|---|---|
| 3 | 2 |
| 1 | |
| 2 | |
| 5 | |
| 10 |
Solution
For access, consult one of our IM Certified Partners.
Problem 3
Clare travels at a constant speed, as shown on the double number line.
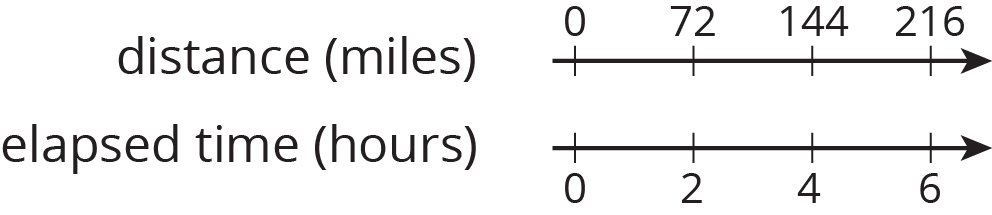
At this rate, how far does she travel in each of these intervals of time? Explain or show your reasoning. If you get stuck, consider using a table.
- 1 hour
- 3 hours
- 6.5 hours
Solution
For access, consult one of our IM Certified Partners.
Problem 4
Lin and Diego travel in cars on the highway at constant speeds. In each case, decide who was traveling faster and explain how you know.
- During the first half hour, Lin travels 23 miles while Diego travels 25 miles.
- After stopping for lunch, they travel at different speeds. To travel the next 60 miles, it takes Lin 65 minutes and it takes Diego 70 minutes.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 2, Lesson 9.)Problem 5
A sports drink recipe calls for \(\frac{5}{3}\) tablespoons of powdered drink mix for every 12 ounces of water. How many batches can you make with 5 tablespoons of drink mix and 36 ounces of water? Explain your reasoning.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 2, Lesson 3.)Problem 6
In this cube, each small square has side length 1 unit.
- What is the surface area of this cube?
- What is the volume of this cube?

Solution
For access, consult one of our IM Certified Partners.
(From Unit 1, Lesson 18.)