Lesson 1
Introducing Ratios and Ratio Language
Lesson Narrative
In this lesson, students use collections of objects to make sense of and use ratio language. Students see that there are several different ways to describe a situation using ratio language. For example, if we have 12 squares and 4 circles, we can say the ratio of squares to circles is \(12:4\) and the ratio of circles to squares is 4 to 12. We may also see a structure that prompts us to regroup them and say that there are 6 squares for every 2 circles, or 3 squares for every one circle (MP7).
Expressing associations of quantities in a context—as students will be doing in this lesson—requires students to use ratio language with care (MP6). Making groups of physical objects that correspond with “for every” language is a concrete way for students to make sense of the problem (MP1).
It is important that in this first lesson students have physical objects they can move around. Later, they will draw diagrams that reflect the same structures and learn to reason with and interpret abstract representations like double number line diagrams and tables. Working with objects that can be physically rearranged in the beginning of the unit can help students make sense of increasingly abstract representations they will encounter as the unit progresses. Students will continue to develop ratio language throughout the unit and will learn about equivalent ratios in a future lesson.
Learning Goals
Teacher Facing
- Comprehend the word “ratio” (in written and spoken language) and the notation $a:b$ (in written language) to refer to an association between quantities.
- Describe (orally and in writing) associations between quantities using the language “For every $a$ of these, there are $b$ of those” and “The ratio of these to those is $a:b$ (or $a$ to $b$).”
Student Facing
Let’s describe two quantities at the same time.
Required Materials
Required Preparation
A few days before this lesson, ask students to bring a personal collection of 10–50 small objects. Examples include rocks, seashells, trading cards, or coins. Bring in your personal collection and display it ahead of time. Think of possible ways to sort your collection. (See the Launch section of the first activity for details.) Prepare a few extra collections for students who don’t bring one.
Learning Targets
Student Facing
- I can write or say a sentence that describes a ratio.
- I know how to say words and numbers in the correct order to accurately describe the ratio.
Glossary Entries
-
ratio
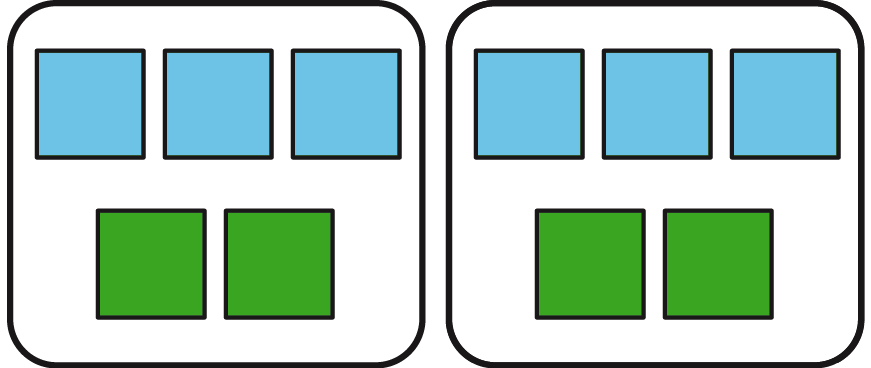
A ratio is an association between two or more quantities.
For example, the ratio \(3:2\) could describe a recipe that uses 3 cups of flour for every 2 eggs, or a boat that moves 3 meters every 2 seconds. One way to represent the ratio \(3:2\) is with a diagram that has 3 blue squares for every 2 green squares.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |