Lesson 3

In this hanger, the weight of the triangle is \(x\) and the weight of the square is \(y\).

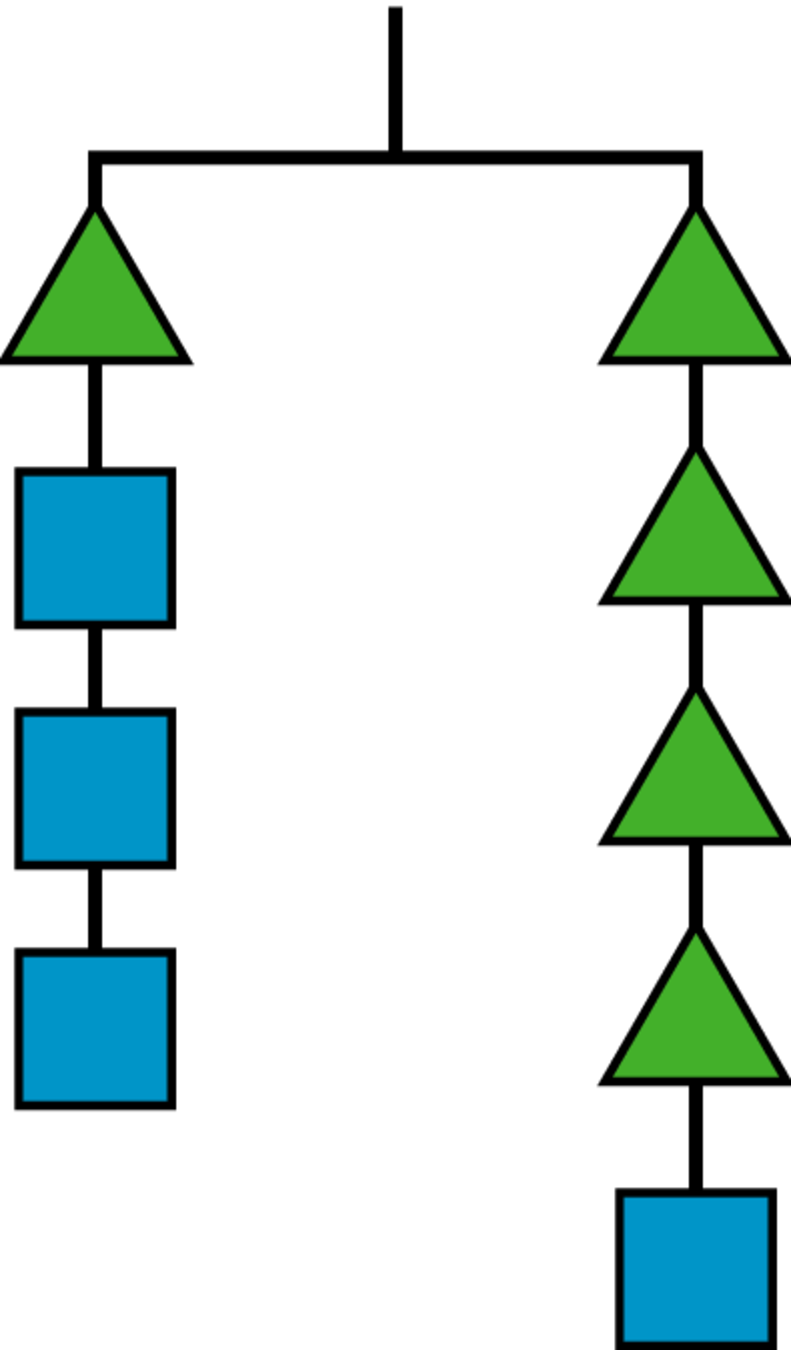
1. Write an equation using \(x\) and \(y\) to represent the hanger.

2. If \(x\) is 6, what is \(y\)?

Andre and Diego were each trying to solve \(2x+6=3x-8\). Describe the first step they each make to the equation.

1. The result of Andre’s first step was \(\text-x+6=\text-8\).
    
    
2. The result of Diego’s first step was \(6=x-8\).
    

1. Complete the table with values for \(x\) or \(y\) that make this equation true: \(3x+y=15\).

   \(x\)	2		6	0	3
   \(y\)		3				0	8




2. Create a graph, plot these points, and find the slope of the line that goes through them.​​​​

   

   

Match each set of equations with the move that turned the first equation into the second.

Select all the situations for which only zero or positive solutions make sense.

Measuring temperature in degrees Celsius at an Arctic outpost each day in January.

The height of a candle as it burns over an hour.

The elevation above sea level of a hiker descending into a canyon.

The number of students remaining in school after 6:00 p.m.

A bank account balance over a year.

The temperature in degrees Fahrenheit of an oven used on a hot summer day.