Lesson 11
On Both of the Lines
11.1: Notice and Wonder: Bugs Passing in the Night (10 minutes)
Warm-up
The purpose of this warm-up is to get students to think about a context that will be explored in the following activity and to reason about the speed, distance, and time each animal is traveling in relation to one another. In the next activity, students will write equations for the bugs and graph these relationships.
Launch
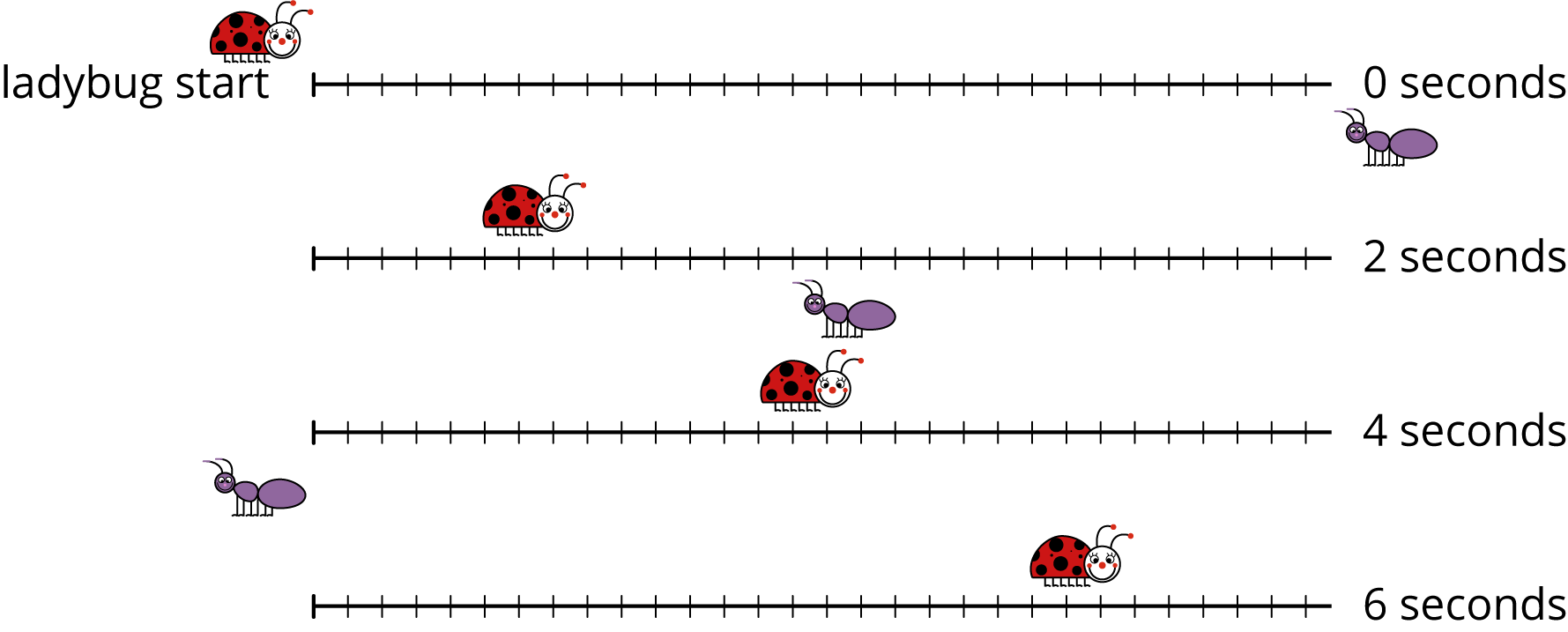
Tell students they will see a picture that shows a ladybug and ant traveling for 6 seconds. Tell students to think of at least one thing they notice and at least one thing they wonder about the picture. Display the problem for all to see and give 1 minute of quiet think time. Ask students to give a signal when they have noticed or wondered about something.
Student Facing
What do you notice? What do you wonder?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share things they noticed and wondered. Record and display their responses for all to see. If any students remember a similar representation from an earlier unit where both the ladybug and the ant started on the same side, you may wish to include how this situation is similar and how it is different.
Important ideas to highlight during the discussion:
- The bugs are moving in opposite directions and at some time in between \(t=2\) and \(t=4\), they pass each other.
- The bugs are moving at a constant speed.
- The ant is moving faster than the ladybug.
11.2: Bugs Passing in the Night, Continued (10 minutes)
Activity
In this task, students find and graph a linear equation given only the graph of another equation, information about the slope, and the coordinates where the lines intersect. The purpose of this task is to check student understanding about the point of intersection in relationship to the context while applying previously learned skills of equation writing and graphing.
Identify students who use different strategies to answer the first problem to share during the whole-class discussion. For example, some students may reason about the equation from an algebraic perspective while others may start by drawing in the graph for the ant based on the provided information. Also, make note of what strategy is most common among students.
Launch
Display the graph from the task statement. Tell students that this activity is about a different ant and ladybug from the warm-up, and we are going to think about their distances using a coordinate plane. Give 4–6 minutes for students to complete the problems followed by a whole-class discussion.
Supports accessibility for: Memory; Conceptual processing
Student Facing
A different ant and ladybug are a certain distance apart, and they start walking toward each other. The graph shows the ladybug’s distance from its starting point over time and the labeled point \((2.5,10)\) indicates when the ant and the ladybug pass each other.

The ant is walking 2 centimeters per second.
- Write an equation representing the relationship between the ant’s distance from the ladybug’s starting point and the amount of time that has passed.
- If you haven’t already, draw the graph of your equation on the same coordinate plane.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is to ensure all students understand both how the labeled point in the task statement relates to the context and how to write and graph an equation from the given information.
Select previously identified students to share their strategy for the first problem, starting with the most common strategy used in the class. Record and display in one place the equations students write. While students may come up with equations like \(\text-2=\frac{d-10}{t-2.5}\), let them know that this approach is valid, but that an equation of the form \(d=\text-2t+15\) will be easier to work with today. Ask each student who shares how they knew to use the point \((2.5, 10)\) when making the equation for the ant.
If students struggled to graph the ant’s path, you may wish to conclude the discussion by asking students for different ways to add the graph of the ant’s distance onto the coordinate plane. For example, some students may say to use the equation figured out in the first problem to plot points and then draw a line through them. Other students may suggest starting from the known point, \((2.5, 10)\), and “working backwards” to figure out that 1 second earlier at 1.5 seconds, the ant would have to be 12 centimeters away since \(10+2=12\).
Design Principle(s): Support sense-making
11.3: A Close Race (15 minutes)
Activity
In previous lessons, students encountered equations with a single variable that had infinitely many solutions. In this activity, students interpret a situation with infinitely many solutions. A race is described using different representations (a table and a description in words). Students graph the relationships given by the descriptions and notice that the lines overlap so that both relationships are true for any pair of values along the graphed line.
Launch
Allow students 7–10 minutes of silent work time followed by a whole-class discussion.
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
Elena and Jada were racing 100 meters on their bikes. Both racers started at the same time and rode at constant speed. Here is a table that gives information about Jada’s bike race:
| time from start (seconds) | distance from start (meters) |
|---|---|
| 6 | 36 |
| 9 | 54 |
- Graph the relationship between distance and time for Jada’s bike race. Make sure to label and scale the axes appropriately.
- Elena traveled the entire race at a steady 6 meters per second. On the same set of axes, graph the relationship between distance and time for Elena’s bike race.
- Who won the race?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The key point for discussion is to connect what students observed about the graph they made to the concept of “infinitely many solutions” encountered in earlier lessons. Graphically, students see that there are situations where two lines align “on top of each other.” We can interpret each point on the line as representing a solution to both Elena’s and Jada’s equations. If \(t\) is the time from start and \(y\) is the distance from the start, the equation for Elena is \(y=6t\). The equation for Jada is also \(y = 6t\). Every solution to Elena’s equation is also a solution to Jada’s equation, and every solution to Jada’s equation is also a solution to Elena's equation. In this way, there are infinitely many points that are solutions to both equations at the same time.
Ensure students clearly understand that just because there are infinitely many points that are solutions, it does not mean that any pair of values will solve both Elena’s and Jada’s equations. In this example, the pair of values must still be related by the equation \(y = 6x\). So, pairs of values like \((1, 6)\), \((10, 60),\) and \(\left( \frac{1}{2}, 3\right)\) are all solutions, but \((1, 8)\) is not.
Lesson Synthesis
Lesson Synthesis
Display a set of axes for all to see. Ask each question one at a time, allowing students time to work through each problem. As students share their responses, add graphs of the lines described to the axes.
- “A line goes through the point \((2, 5)\) and has a slope of 1.5. What is an equation for this line?” (\(y = 1.5x + 2\))
- “A second line goes through the point \((2,5)\) and has a \(y\)-intercept of \((0,10)\). What is an equation for this line?” (\(y = \text-2.5x+10\))
- “What does the point \((2,5)\) represent for these lines?” (The pair of values that is true in both situations.)
- "A third line goes through this same point. How would that show up in a table representing the relationship for the third line?" (The number 2 would be in the \(x\) column right next to the number 5 in the \(y\) column.)
11.4: Cool-down - Saving Cash (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The solutions to an equation correspond to points on its graph. For example, if Car A is traveling 75 miles per hour and passes a rest area when \(t = 0\), then the distance in miles it has traveled from the rest area after \(t\) hours is
\(\displaystyle d = 75t\)
The point \((2, 150)\) is on the graph of this equation because \(150 = 75 \boldcdot 2\): two hours after passing the rest area, the car has traveled 150 miles.
If you have two equations, you can ask whether there is an ordered pair that is a solution to both equations simultaneously. For example, if Car B is traveling towards the rest area and its distance from the rest area is
\(\displaystyle d = 14 - 65t\)
We can ask if there is ever a time when the distance of Car A from the rest area is the same as the distance of Car B from the rest area. If the answer is “yes”, then the solution will correspond to a point that is on both lines.
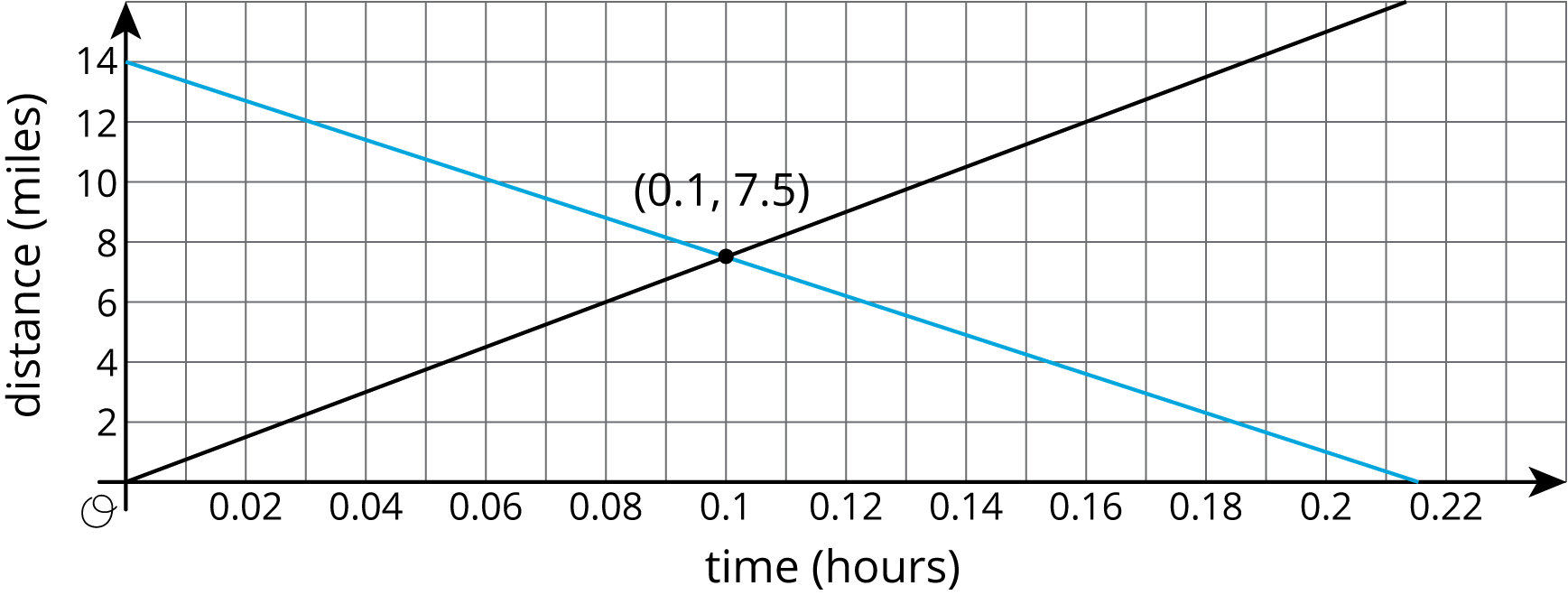
Looking at the coordinates of the intersection point, we see that Car A and Car B will both be 7.5 miles from the rest area after 0.1 hours (which is 6 minutes).
Now suppose another car, Car C, had also passed the rest stop at time \(t=0\) and traveled in the same direction as Car A, also going 75 miles per hour. It's equation would also be \(d=75t\). Any solution to the equation for Car A would also be a solution for Car C, and any solution to the equation for Car C would also be a solution for Car A. The line for Car C would land right on top of the line for Car A. In this case, every point on the graphed line is a solution to both equations, so that there are infinitely many solutions to the question “when are Car A and Car C the same distance from the rest stop?” This would mean that Car A and Car C were side by side for their whole journey.
When we have two linear equations that are equivalent to each other, like \(y = 3x+2\) and \(2y = 6x +4\), we will get two lines that are “right on top” of each other. Any solution to one equation is also solution to the other, so these two lines intersect at infinitely many points.