Lesson 6
Strategic Solving
6.1: Equal Perimeters (5 minutes)
Warm-up
The purpose of this activity is for students to begin building linear equations and solving them.
Launch
Arrange students in groups of 2. Give students 2 minutes quiet think time, then 2 minutes to discuss their solutions with a partner. Instruct groups to explain to each other how they came up with expressions and an equation to represent the situation.
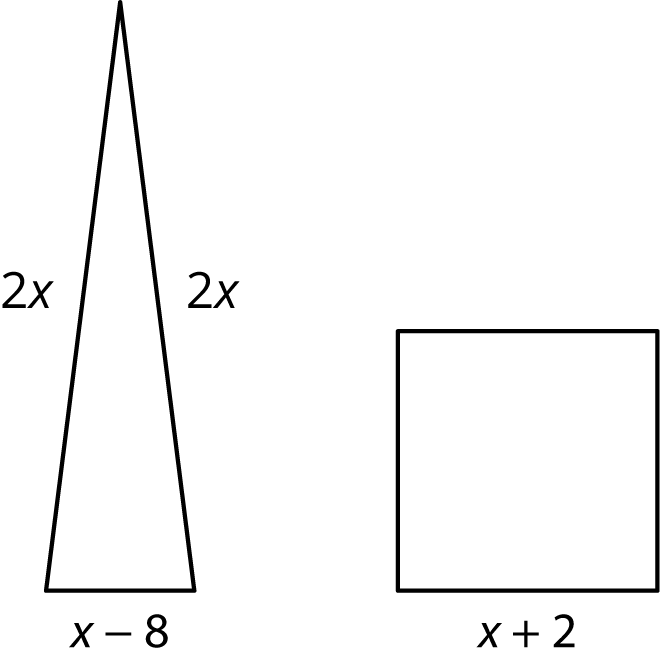
Student Facing
The triangle and the square have equal perimeters.
- Find the value of \(x\).
- What is the perimeter of each of the figures?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask groups to share their strategies for solving the question. Consider asking some of the following questions:
- “What expression represents the perimeter of the triangle? The perimeter of the square?” (The expression for perimeter of the triangle is \(5x-8\), and the perimeter of the square is \(4(x+2)\).)
- “What was your strategy in making an equation?” (If both perimeters are the same, we can say their expressions are equal.)
- “What does \(x\) mean in the situation?” (It means an unknown value. None of the sides or perimeter is represented by \(x\), so we cannot say it represents a specific thing on the figures.)
- “Looking at the figures, are there any values that \(x\) could not be? Explain your reasoning.” (Since the triangles have sides that are \(2x\), \(x\) cannot be 0 or a negative value. Triangles cannot have sides with 0 or negative side lengths. Since the third side is \(x-8\), we can use this same reasoning to realize that \(x\) must actually be greater than 8.)
- “How does this information help when solving?” (If I make a mistake in my solution and get a value of \(x\) that is less than or equal to 8, then I know immediately that my answer is not reasonable and I can try to find my error.)
6.2: Predicting Solutions (10 minutes)
Activity
The purpose of this activity is to shift the focus from solving an equation to thinking about what it means for a number to be a solution of an equation. Students inspect each equation, looking at the structure, the signs, and the operations in it to decide if the solution is positive, negative, or zero. Some questions are paired with another question (for example, the last two questions) so students can take advantage of their thinking from one to the next.
Launch
Arrange students in groups of 2.
Display the equation \(5x=6x\) for all to see.
Ask students, "How might we know whether \(x\) is a positive number, negative number, or zero, without solving the equation?" (The variables can be combined into one term, but there are no constant terms. That means eventually the variable term has to equal 0, so \(x\) must be 0.)
Display the equation \(5x=\text-16.5\) for all to see and ask the same question. (Without solving, we can see that a positive number of \(x\)s has to equal a negative value, so \(x\) must be a negative number.)
Instruct students to inspect each equation carefully and use reasoning to answer the questions in the activity rather than trying to solve each equation for a specific value. Give 5 minutes of quiet think time, and then ask students to compare their work with their partner. For any questions they disagree on, students should work to reach an agreement.
Supports accessibility for: Memory; Conceptual processing
Design Principle(s): Cultivate conversation; Support sense-making
Student Facing
Without solving, identify whether these equations have a solution that is positive, negative, or zero.
- \(\frac{x}{6}=\frac{3x}{4}\)
- \(7x=3.25\)
- \(7x=32.5\)
- \(3x+11=11\)
- \(9-4x=4\)
- \(\text-8+5x=\text-20\)
- \(\text-\frac12(\text-8+5x)=\text-20\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
For each equation, invite groups to share how they decided if the solution was positive, negative, or zero. After each group shares, ask if any other group reasoned about the problem in a different way and invite them to share their reasoning.
The purpose of this discussion is for students to practice talking about equations, the operations within them, and use logical thinking. There is no need to try and formally generalize student thinking for all cases at this time. In later grades, students will continue the work started here looking for structure in equations.
6.3: Which Would You Rather Solve? (20 minutes)
Activity
The purpose of this activity is for students to think about what they see as “least difficult” and “most difficult” when looking at equations and to practice solving equations. Students also discuss strategies for dealing with “difficult” parts of equations.
Launch
Keep students in the same groups of 2. Give students 3–5 minutes quiet think time to get started and then 5–8 minutes to discuss and work with their partner. Leave ample time for a whole-class discussion.
Supports accessibility for: Memory; Conceptual processing
Student Facing
Here are a lot of equations:
A. \(\text{-} \frac56(8+5b)=75+\frac53 b\)
B. \(\text-\frac12(t+3)-10=\text-6.5\)
C. \(\frac{10-v}{4}=2(v+17)\)
D. \(2(4k+3)-13=2(18-k)-13\)
E. \(\frac{n}{7}-12=5n+5\)
F. \(3(c-1)+2(3c+1)=\text-(3c+1)\)
G. \(\frac{4m-3}4=\text{-}\frac{9+4m}8\)
H. \(p-5(p+4)=p-(8-p)\)
I. \(2(2q+1.5)=18-q\)
J. \(2r+49=\text{-}8(\text{-}r-5)\)
- Without solving, identify 3 equations that you think would be least difficult to solve and 3 equations you think would be most difficult to solve. Be prepared to explain your reasoning.
- Choose 3 equations to solve. At least one should be from your "least difficult" list and one should be from your "most difficult" list.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Mai gave half of her brownies, and then half a brownie more, to Kiran. Then she gave half of what was left, and half a brownie more, to Tyler. That left her with one remaining brownie. How many brownies did she have to start with?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is for students to discuss strategies for solving different types of equations. Some students may have thought that an equation was in the “least difficult” category, while others thought that the same equation was in the “most difficult” category. Remind students that once you feel confident about the strategies for solving an equation, it may move into the “least difficult” category, and recognizing good strategies takes practice and time.
Poll the class for each question as to whether they placed it in the “most difficult” category, “least difficult” category, or if it was somewhere in the middle. Record and display the results of the poll for all to see.
For questions with a split vote, have a group share something that was difficult about it and something that made it seem easy. If there are any questions that everyone thought would be more difficult or everyone thought would be less difficult, ask students why it seemed that way. Ask students, “Were there any equations that were more difficult to solve than you expected? Were there any that were less difficult to solve than you expected?”
Consider asking some of the following questions to further the discussion:
- “For equation A, what could we do to eliminate the fraction?” (Multiply each side by the common denominator of 6. Then the terms will all have integer coefficients.)
- “Which other equations could we use this strategy for?” (Any equations that had fractions, such as B, C, E, and G.)
- “What steps do you need to do to solve equation D? Which other equations are like this one?” (There is a lot of distributing and collecting like terms. F and H also have to distribute several times.)
- “What other strategies or steps did you use in solving the equations?”
Design Principle(s): Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Instruct students to write an equation with a variable and a constant term on each side that they would look at and consider difficult to solve.
Select several students' equations to display for all to see. Discuss with students:
- “What are some things these equations have in common that might be considered difficult to solve?” (Answers vary, but students may use fractions, decimals, distribution, and negatives to increase level of difficulty.)
- “What strategies do we know for solving equations that have each of these things?” (For fractions, we can find a common denominator and multiply each side of the equation by the denominator to eliminate the fractions. For distribution, we can make sure to collect like terms before we do other steps. For use of decimals and negatives, we can make sure we perform calculations carefully.)
Choose one of the displayed equations for students to solve. Have them compare solutions with a partner. Ask students, “Did any of you use different strategies for solving this equation than your partner? How many of you followed the same solution path?” Share a correct solution with the class so they can compare their solutions.
6.4: Cool-down - Think Before You Step (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Sometimes we are asked to solve equations with a lot of things going on on each side. For example,
\(x-2(x+5)=\dfrac{3(2x-20)}{6}\)
This equation has variables on each side, parentheses, and even a fraction to think about. Before we start distributing, let's take a closer look at the fraction on the right side. The expression \(2x-20\) is being multiplied by 3 and divided by 6, which is the same as just dividing by 2, so we can re-write the equation as
\(x-2(x+5)=\dfrac{2x-20}{2}\)
But now it’s easier to see that all the terms on the numerator of right side are divisible by 2, which means we can re-write the right side again as
\(x-2(x+5)=x-10\)
At this point, we could do some distribution and then collect like terms on each side of the equation. Another choice would be to use the structure of the equation. Both the left and the right side have something being subtracted from \(x\). But, if the two sides are equal, that means the "something" being subtracted on each side must also be equal. Thinking this way, the equation can now be re-written with less terms as
\(2(x+5)=10\)
Only a few steps left! But what can we tell about the solution to this problem right now? Is it positive? Negative? Zero? Well, the 2 and the 5 multiplied together are 10, so that means the 2 and the \(x\) multiplied together cannot have a positive or a negative value. Finishing the steps we have:
\(\begin{align} 2(x+5)&=10\\ x+5&=5&&\text{Divide each side by 2}\\ x &=0&&\text{Subtract 5 from each side}\\ \end{align}\)
Neither positive nor negative. Just as predicted.