Lesson 3
Balanced Moves
3.1: Matching Hangers (10 minutes)
Warm-up
The purpose of this warm-up is for students to revisit ideas they learned in the previous lesson about balanced hangers:
- You can add or subtract the same thing on each side and the hanger stays in balance.
- You can divide each side by the same number and the hanger stays in balance.
Launch
Give students 2 minutes of quiet work time followed by a whole-class discussion.
Student Facing
Figures A, B, C, and D show the result of simplifying the hanger in Figure A by removing equal weights from each side.
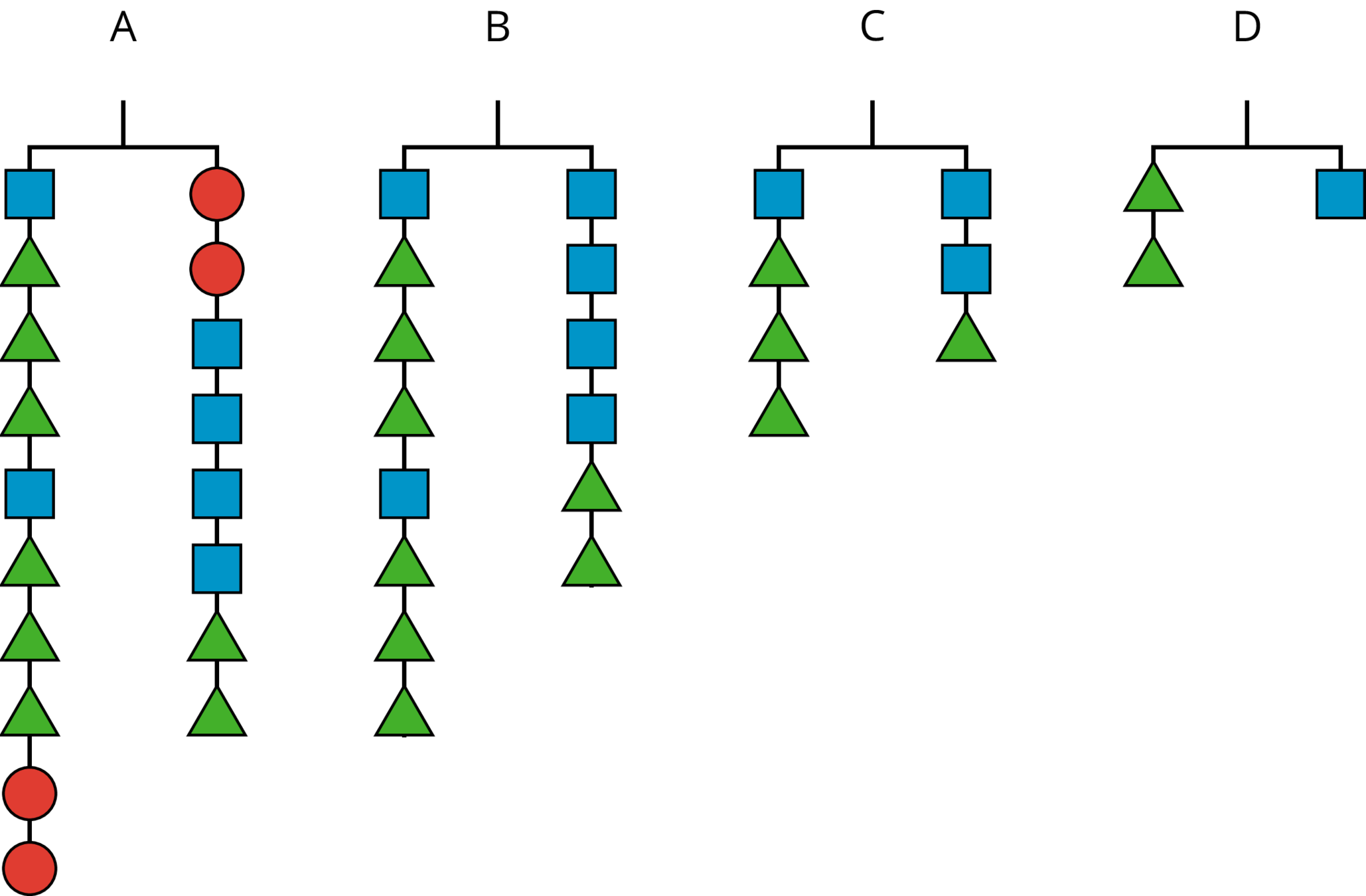
Here are some equations. Each equation represents one of the hanger diagrams.
\(2(x + 3y) = 4x + 2y\)
\(2y = x\)
\(2(x + 3y) + 2z = 2z + 4x + 2y\)
\(x + 3y = 2x + y\)
-
Write the equation that goes with each figure:
A:
B:
C:
D:
- Each variable (\(x\), \(y\), and \(z\)) represents the weight of one shape. Which goes with which?
- Explain what was done to each equation to create the next equation. If you get stuck, think about how the hangers changed.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may think a variable stands for more than one object. Tell these students that a variable only stands for one object, as it also only represents one number.
Activity Synthesis
Ask students to explain how they decided on the matching equation. As students discuss the final questions, highlight responses that emphasize the same objects being removed from each side creates the next figure in line. The exception to this is the move from Hanger B to Hanger C, where the number of objects on each side is halved. Ask students to explain why this is an okay move, even though different objects are being removed from each side (1 square and 3 triangles on the left, 2 squares and 1 triangle on the right). Refer to MLR 2 (Collect and Display).
3.2: Matching Equation Moves (15 minutes)
Activity
In this activity, students match a card with two equations to another card describing the move that turns the first equation into the second. The goal is to help students think about equations the same way they have been thinking about hangers: objects where equality is maintained so long as the same move is made on each side. Additionally, this is the first activity where students encounter equation moves involving negative numbers, which is not possible when using hangers.
Launch
Review with students what we know about equations based on reasoning about hangers:
- We can add the same quantity to each side, and the equation is still true (the hanger is still in balance).
- We can subtract the same quantity from each side, and the equation is still true.
- We can double or triple or halve or third the things that appear on each side, and the equation is still true. More generally, we can multiply the number of things on each side by the same number.
Tell students that hanger diagrams are really only useful for reasoning about positive numbers, but the processes above also work for negative numbers. Negative numbers are just numbers, and they have to follow the same rules as positive numbers. In fact, if we allow negative numbers into the mix, we can express any maneuver with one of two types of moves:
- Add the same thing to each side. (The “thing” could be negative.)
- Multiply each side by the same thing. (The “thing” could be a fraction less than 1.)
Arrange students in groups of 2. Give each group 12 pre-cut slips from the blackline master. Give 3–4 minutes for partners to match the numbered slips with the lettered slips then 1–2 minutes to trade places with another group and review each other’s work. Ask partners who finish early to write down on a separate sheet of paper what the next move would be for each of the numbered cards if the goal were to solve for \(x\). Follow with a whole-class discussion.
Supports accessibility for: Conceptual processing; Organization
Student Facing
Your teacher will give you some cards. Each of the cards 1 through 6 show two equations. Each of the cards A through E describe a move that turns one equation into another.
- Match each number card with a letter card.
- One of the letter cards will not have a match. For this card, write two equations showing the described move.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The goal of this discussion is to get students using the language of equations and describing the changes happening on each side when solving. Ask:
- “What is a move you could do to the equation \(7=2x\) on card 1 that would result in an equation of the form \(x=\underline{ }\)? What is another move that would also work?” (Multiply each side by \(\frac12\). Divide each side by 2.)
- “Which numbered card was the most challenging to match?” (Card 2, because it at first I only looked at the \(x\)-terms and thought the move involved a change of \(8x\).)
- “Does anyone have a value for \(x\) that would solve one of the numbered cards? How did you figure it out?” (\(x=2\) is a solution for card 5. I added 3 to each side and then multiplied each side by \(\frac14\).)
End the discussion by inviting groups to share the equations they wrote for card 6 and describe how they match the move "add \(3x\) to each side."
Design Principle(s): Optimize output (for generalization)
3.3: Keeping Equality (10 minutes)
Activity
The purpose of this activity is to get students thinking about strategically solving equations by paying attention to their structure. Distribution first versus dividing first is a common point of divergence for students as they start solving.
Identify students who choose different solution paths to solve the last two problems.
Launch
Arrange students in groups of 2. Give students 2 minutes quiet think time for problem 1, then 3–5 minutes partner time to discuss problem 1 and complete the other problems. Follow with a whole-class discussion.
Design Principle(s): Maximize meta-awareness; Cultivate conversation
Student Facing
- Noah and Lin both solved the equation \(14a=2(a-3)\).
Do you agree with either of them? Why?
Noah's solution:
\(\begin{align*} 14a&=2(a-3) \\ 14a&=2a-6 \\ 12a&=\text-6 \\ a&=\text-\frac12 \\ \end{align*}\)
Lin's solution:
\(\begin{align} 14a&=2(a-3) \\ 7a&=a-3\\ 6a&=\text-3\\a&=\text-\frac12 \end{align}\)
- Elena is asked to solve \(15 - 10x = 5(x + 9)\). What do you recommend she does to each side first?
- Diego is asked to solve \(3x -8 = 4(x + 5)\). What do you recommend he does to each side first?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
In a cryptarithmetic puzzle, the digits 0–9 are represented with letters of the alphabet. Use your understanding of addition to find which digits go with the letters A, B, E, G, H, L, N, and R.
HANGER + HANGER + HANGER = ALGEBRA
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may not distribute or collect like terms before performing the same operation on each side.
Activity Synthesis
Have previously identified groups share the different solution paths they chose for solving the last two questions.
To highlight the different strategies, ask:
- “What are the advantages of choosing to distribute first? To divide first?” (Answers vary. Distributing first eliminates confusion about which terms can be subtracted from each side. Dividing first makes the numbers smaller and easier to mentally calculate.)
- “What makes it easier to distribute versus divide first on the last question?” (Dividing by 4 before distributing will result in non-integer terms, which can be harder to add and subtract mentally.)
- “Is one path more ‘right’ than another?” (No. As long as we follow valid steps, like adding or multiplying the same thing to each side of an equation, the steps are right and will give a correct solution.)
Lesson Synthesis
Lesson Synthesis
Display the equation \(6x + 12 = 10x - 4\) for all to see. Tell students to think of three different things they could do to each side of the question but still maintain equality. Invite students to share their moves. Possible responses include:
- subtract \(6x\) from each side
- add 4 to each side
- divide each side by 2
Ask students, "If you made a mistake when solving this equation and thought that \(x=2\), how would you be able to tell?" (If I put 2 into the equation, I would get that \(24=16\), which isn't true.)
3.4: Cool-down - More Matching Moves (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
An equation tells us that two expressions have equal value. For example, if \(4x+9\) and \(\text-2x-3\) have equal value, we can write the equation
\(4x + 9 = \text-2x - 3\)
Earlier, we used hangers to understand that if we add the same positive number to each side of the equation, the sides will still have equal value. It also works if we add negative numbers! For example, we can add -9 to each side of the equation.
\(\begin{align} 4x+9+\text-9 &= \text-2x-3+\text-9 &&\text{add \(\text-9\) to each side}\\ 4x &= \text-2x-12 && \text{combine like terms} \end{align}\)
Since expressions represent numbers, we can also add expressions to each side of an equation. For example, we can add \(2x\) to each side and still maintain equality.
\(\begin{align} 4x+2x &= \text-2x-12 +2x && \text{add \(2x\) to each side} \\ 6x &= \text-12 && \text{combine like terms} \end{align}\)
If we multiply or divide the expressions on each side of an equation by the same number, we will also maintain the equality (so long as we do not divide by zero).
\(\begin{align} 6x\boldcdot \frac16=\text-12\boldcdot \frac16 && \text{multiply each side by }\frac16 \end{align}\)
or
\(\begin{align} 6x\div6=\text-12\div6 && \text{divide each side by 6} \end{align}\)
Now we can see that \(x = \text-2\) is the solution to our equation.
We will use these moves in systematic ways to solve equations in future lessons.