Lesson 2
Keeping the Equation Balanced
2.1: Notice and Wonder: Hanging Socks (5 minutes)
Warm-up
The purpose of this warm-up is to give students an opportunity to ground their understanding of equality in the context of weight, which is a context that will be used throughout the lesson.
Launch
Tell students they will look at a picture, and their job is to think of at least one thing they notice and at least one thing they wonder about the picture. Display the problem for all to see and give 1 minute of quiet think time. Ask students to give a signal when they have noticed or wondered about something.
Student Facing
What do you notice? What do you wonder?

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their ideas. Record and display the responses for all to see. In the interest of time, you can ask if anything students wondered was a “why” question, meaning the question begins with the word why. Refer to MLR 2 (Collect and Display).
If not brought up during the first part of the discussion, ask students why they think the left hanger is balanced while the right hanger is unbalanced. Students should understand that a hanger will only balance if the weight of the unknown objects in both socks is the same. If they are not the same, then the heavier side is lower than the lighter side.
2.2: Hanging Blocks (10 minutes)
Activity
The purpose of this task is for students to understand and explain why they can add or subtract expressions from each side of an equation and still maintain the equality, even if the value of those expressions are not known. Both problems have shapes with unknown weight on each side to promote students thinking about unknown values in this way before the transition to equations.
While the focus of this activity is on the relationship between both sides of the hanger and not equations, some students may start the second problem by writing and solving an equation to find the weight of a square. While students are working, identify those using equations and those not using equations to answer the second problem during the whole-class discussion.
Launch
Display the problem image for all to see. Tell students that this is a hanger problem similar to the one in the warm-up, only instead of the weights hidden inside socks, each block type represents a different weight. Give 5 minutes of quiet work time followed by a whole-class discussion.
If using the digital activity, introduce the hanger problem to set the context and connection to the warm-up. Give students individual work time to figure out the weights and use the applet to check their work.
Supports accessibility for: Conceptual processing; Visual-spatial processing
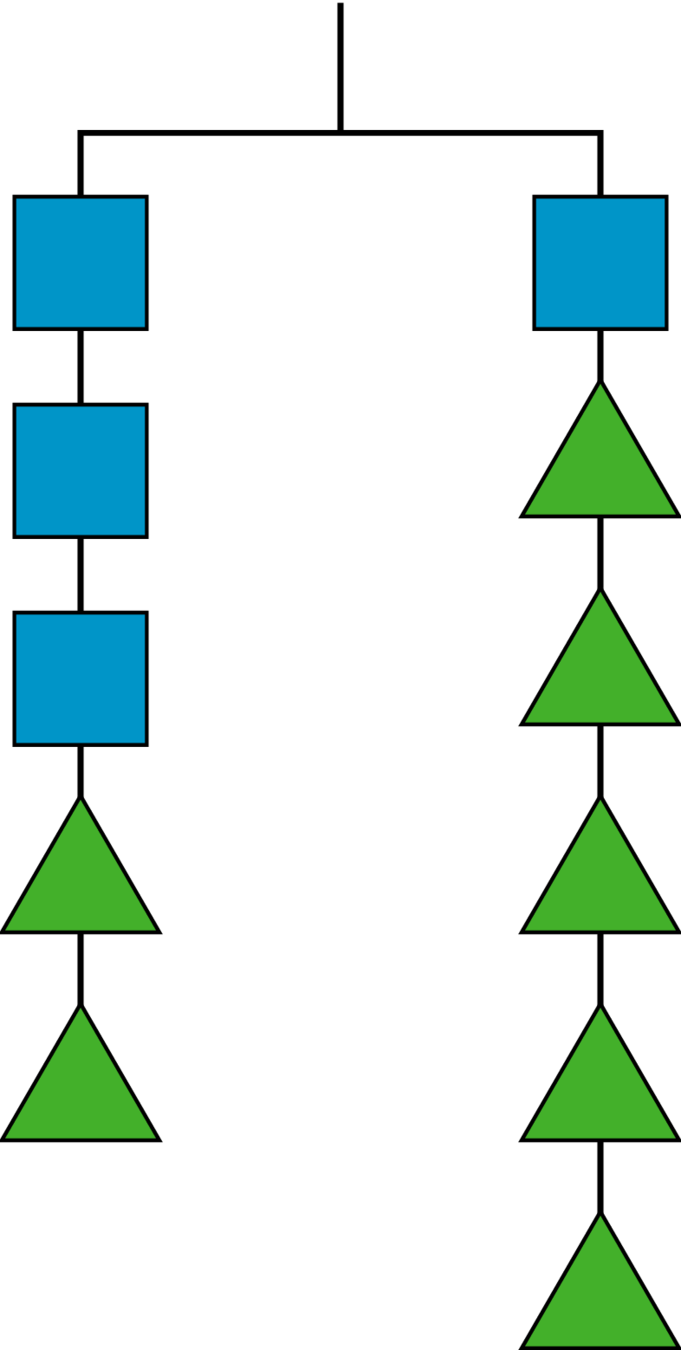
Student Facing
This picture represents a hanger that is balanced because the weight on both sides is the same.
-
Elena takes two triangles off of the left side and three triangles off of the right side. Will the hanger still be in balance, or will it tip to one side? Which side? Explain how you know.
-
Use the applet to see if your answer to question [1] was correct. Can you find another way to make the hanger balance?
-
If a triangle weighs 1 gram, how much does a square weigh? After you make a prediction, use the applet to see if you were right. Can you find another pair of values that makes the hanger balance?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Try your own Hanger Balances!
Student Response
For access, consult one of our IM Certified Partners.
Launch
Display the problem image for all to see. Tell students that this is a hanger problem similar to the one in the warm-up, only instead of the weights hidden inside socks, each block type represents a different weight. Give 5 minutes of quiet work time followed by a whole-class discussion.
If using the digital activity, introduce the hanger problem to set the context and connection to the warm-up. Give students individual work time to figure out the weights and use the applet to check their work.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Student Facing
This picture represents a hanger that is balanced because the weight on each side is the same.
- Elena takes two triangles off of the left side and three triangles off of the right side. Will the hanger still be in balance, or will it tip to one side? Which side? Explain how you know.
- If a triangle weighs 1 gram, how much does a square weigh?

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
In the first question, students may think the hanger will stay in balance since removing the 5 triangles results in three shapes on each side.
Activity Synthesis
Begin the discussion by asking if students think the hanger will stay in balance, tip to the left, or tip to the right. Select 2–3 students to explain their vote. Make sure the class understands that removing unequal amounts of weight from the two sides results in the hanger tipping before moving on. Use MLR 2 (Collect and Display) to capture student reasoning about it being okay to add or remove terms of the same “size” from both sides of an equation.
For the second question, select previously identified students to explain their answers, with the students who used equations going last. Record and display the specific equations the selected students wrote for all to see, such as \(x+x+x+1+1=x+1+1+1+1+1\) or \(3x+2=x+5\), and use it to help the class visualize how that student solved for the weight of a square.
The outcome of this discussion should be that it is okay to add or remove terms of the same “size” from both sides of an equation, and the sides will still be equal. This can be thought of in terms of shapes hanging on hangers, where you can remove one square from both sides or add two triangles to both sides, and the hanger will stay in balance. Equations are a more abstract representation of this, but the same concept holds: you can remove one \(x\) from both sides or add two 3s to both sides and the equation is still true with the left side equal to the right side. Removing equal weights from both sides can leave the hanger with 2 squares on the left and 3 triangles (or just 3) on the right. In equation form, this is the same as \(2x = 3\). Finally, you can halve the amount of weight on both sides of the hanger and keep it in balance, which is the same as multiplying \(2x = 3\) by \(\frac{1}{2}\) (or dividing both sides by 2).
Design Principle(s): Support sense-making
2.3: More Hanging Blocks (15 minutes)
Activity
Building on the previous activity, students now solve two more hanger problems and write equations to represent each hanger. In the first problem, the solution is not an integer, which will challenge any student who has been using guess-and-check in the previous activities to look for a more efficient method. In the second problem, the solution is any weight, which is a preview of future lessons when students purposefully study equations with one solution, no solution, and infinite solutions. The goal of this activity is for students to transition their reasoning about solving hangers by maintaining the equality of each side to solving equations using the same logic. In future lessons, students will continue to develop this skill as equations grow more complex culminating in solving systems of equations at the end of this unit.
As students work, identify those using strategies to find the weight of one square/pentagon that do not involve an equation. For example, some students may cross out pairs of shapes that are on each side (such as one circle and one square from each side of hanger A) to reason about a simpler problem while others may replace triangles with 3s and circles with 6s first before focusing on the value of 1 square. This type of reasoning should be encouraged and built upon using the language of equations.
Launch
Arrange students in groups of 2. Give 5 minutes of quiet work time followed by partner discussion. Let students know that they should be prepared to share during the whole-class discussion, so they should make sure their partner understands and agrees with their solution.
If students use the digital activity, the applet provides a way for students to check solutions. Encourage students to work individually (most likely they will need paper/pencil to work these problems) and then check their thinking using the digital applet. After students have had 5 minutes to work alone and with the applet, give them time to discuss their thinking with a partner before the whole-class discussion.
Supports accessibility for: Conceptual processing
Student Facing
A triangle weighs 3 grams, and a circle weighs 6 grams.
-
Find the weight of a square.
-
Find the weight of a pentagon.
-
Write an equation to represent each hanger.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Try your own!
Launch
Arrange students in groups of 2. Give 5 minutes of quiet work time followed by partner discussion. Let students know that they should be prepared to share during the whole-class discussion, so they should make sure their partner understands and agrees with their solution.
If students use the digital activity, the applet provides a way for students to check solutions. Encourage students to work individually (most likely they will need paper/pencil to work these problems) and then check their thinking using the digital applet. After students have had 5 minutes to work alone and with the applet, give them time to discuss their thinking with a partner before the whole-class discussion.
Supports accessibility for: Conceptual processing
Student Facing
A triangle weighs 3 grams and a circle weighs 6 grams.
-
Find the weight of a square in Hanger A and the weight of a pentagon in
Hanger B. - Write an equation to represent
each hanger.

Student Response
For access, consult one of our IM Certified Partners.
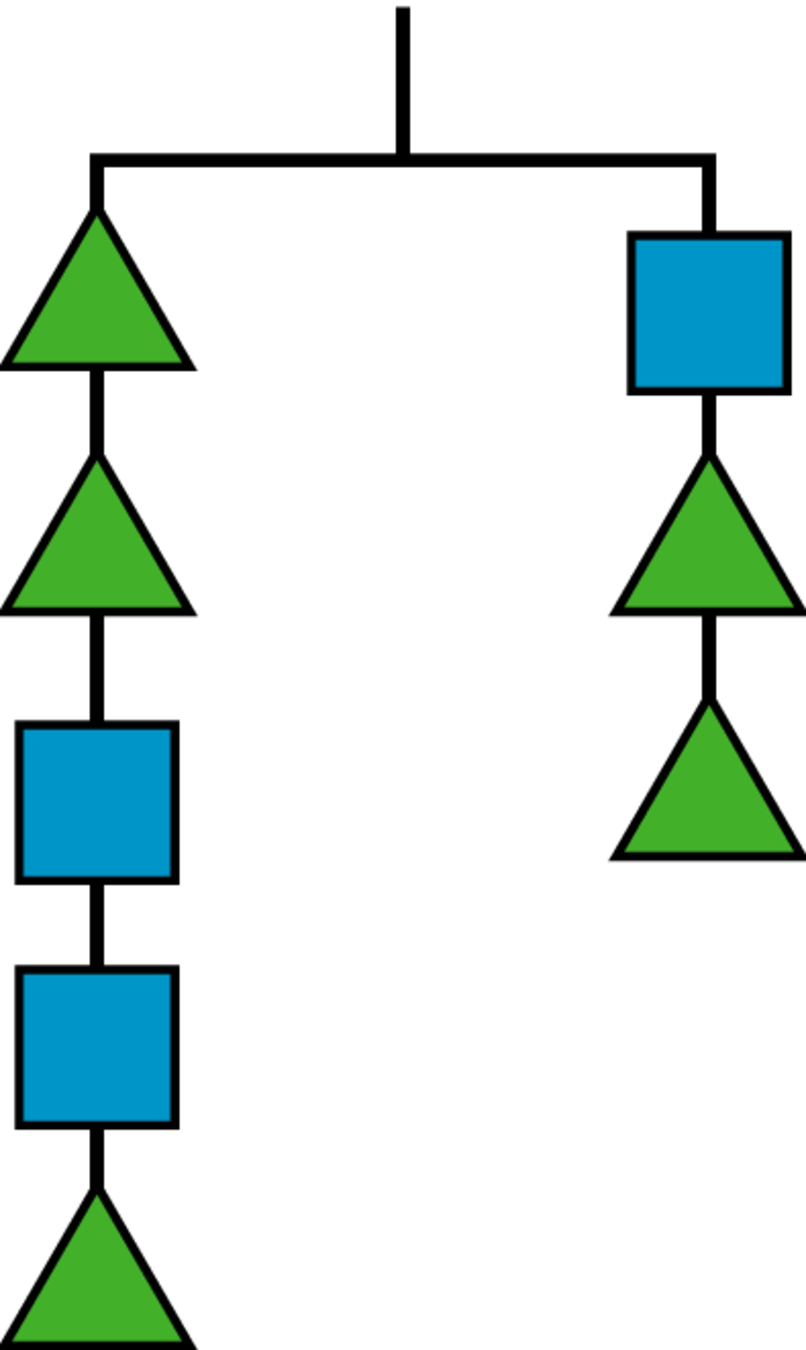
Student Facing
Are you ready for more?
What is the weight of a square on this hanger if a triangle weighs 3 grams?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Triangles weigh 3 grams in this activity instead of 1 gram as in the previous activity.
Activity Synthesis
Select previously identified students to share their strategies for finding the unknown weight without using an equation. Ask students to be clear how they are changing each side of the hanger equally as they share their solutions.
Next, record the equations written by students for each hanger and display for all to see in two lists. Assign half the class to the list for Hanger A and the other half to the list for Hangar B. Give students 1–2 minutes to examine the equations for their assigned hanger and be prepared to explain how different pairs of equations are related. The goal here is for student to use the language they developed with the hangers (e.g., “remove 6 from each side”) on equations.
For example, for Hanger A, you might contrast \(3 + 6 + 6 +6 = 4x+ 6\) with \(21 + x = 6 + 5x\). Possible student responses:
- Removing an \(x\) from each side of the second equation would result in the first equation.
- \(x = 3.75\) grams makes both equations true.
- You can subtract 6s from the sides of each equation and they are still both true.
For Hanger B, examining equations should illuminate why it is impossible to know the weight of the unknown shape. If we start with \(6+6+x+x = x+x+3+3+6\) and keep removing things of equal weight from each side, we might end up with an equation like \(2x=2x\). Any value of \(x\) will work to make this equation true. For example if \(x\) is 10, then the equation is \(20=20\). It is also possible to keep removing things of equal weight from each side and end up with an equation like \(6 = 6\), which is always true.
Design Principle(s): Optimize output; Cultivate conversation
Lesson Synthesis
Lesson Synthesis
The purpose of this discussion is to have students revisit the warm-up and connect it to the activities, reflecting on why the hanger is an appropriate and helpful analogy for an equation.
Ask these questions:
- “In the warm-up we wondered why one hanger was slanted, whether there were weights in one blue sock that made it heavier than the other, whether the crooked hanger would straighten out if another sock was added to the other side (add any other pertinent things your students wondered). How would you answer these questions now?”
- “What is an equation? What does the equal sign in an equation tell you?” (An equation is a statement that two expressions have the same value. The equal sign tells you that the expressions on either side must have the same value, however that value is measured—as a count of objects, a measurement like 10 miles or 6 seconds, or numbers without units.)
- “What features do balanced hangers and equations have in common?” (Both representations have sides that are equal in value, even if the actual value of a side is unknown. Each side can contain numbers we do not know in the form of either shapes or variables. Changing the value of one side of a hanger or equations means changing the value of the other side by the same amount.)
- “You saw an example of a hanger where the unknown weight could not be determined. Can you design your own hanger like this one? How would you think about the weights needed on each side?” (If students completed the extension, you might ask them to also design a hanger with no solution.)
2.4: Cool-down - Changing Blocks (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
If we have equal weights on the ends of a hanger, then the hanger will be in balance. If there is more weight on one side than the other, the hanger will tilt to the heavier side.

We can think of a balanced hanger as a metaphor for an equation. An equation says that the expressions on each side have equal value, just like a balanced hanger has equal weights on each side.
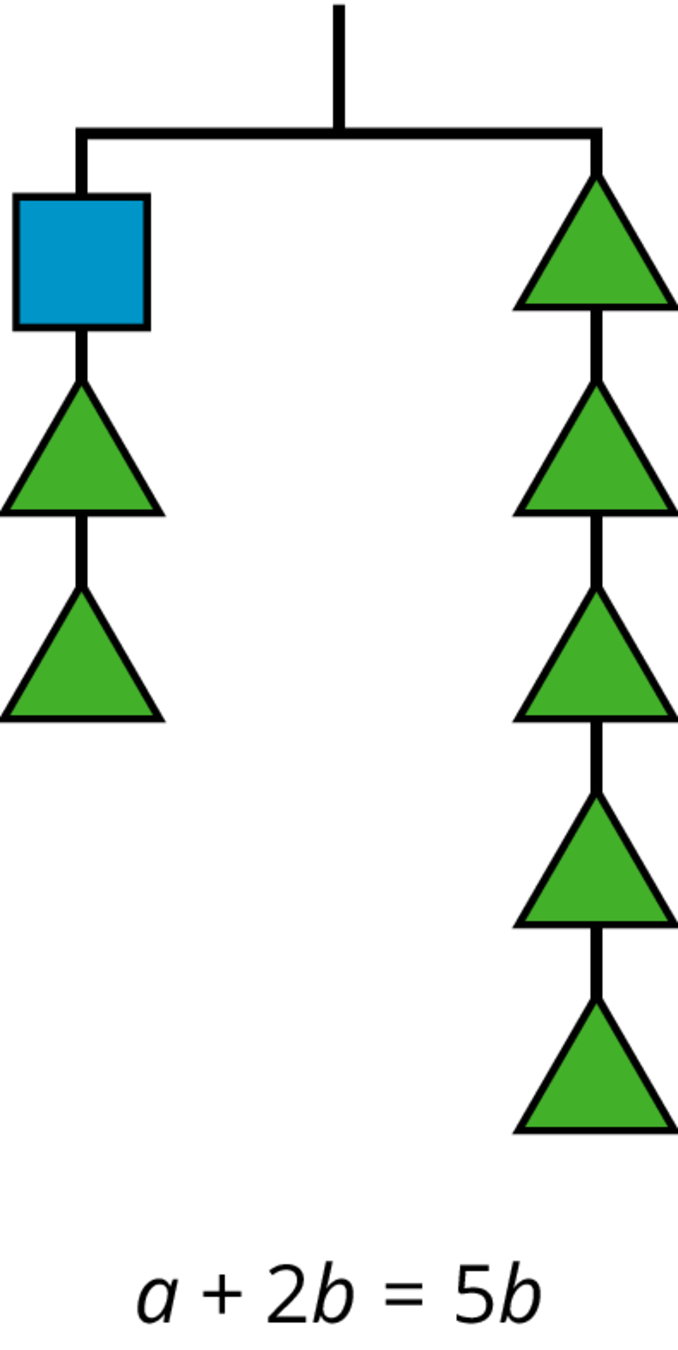
If we have a balanced hanger and add or remove the same amount of weight from each side, the result will still be in balance.
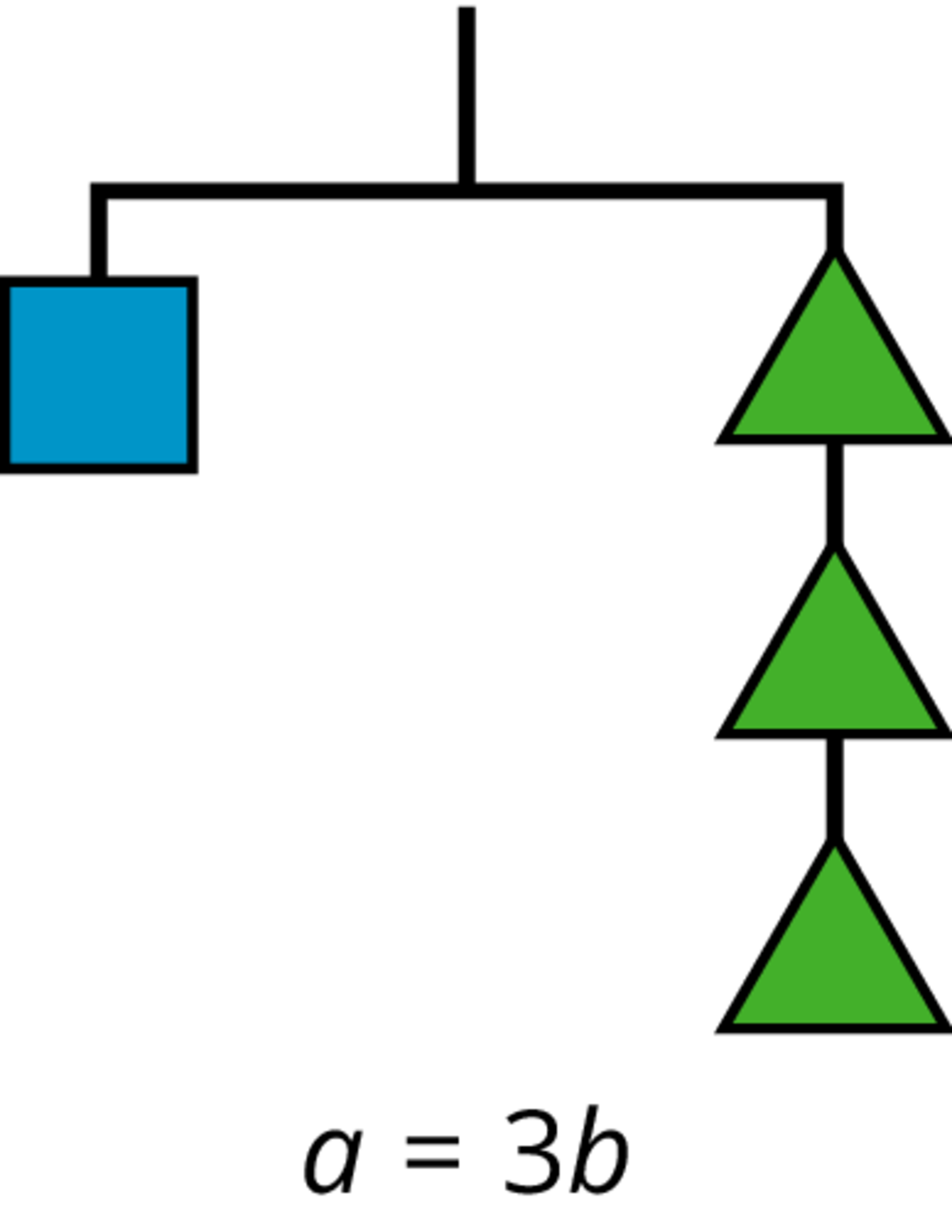
We can do these moves with equations as well: adding or subtracting the same amount from each side of an equation maintains the equality.