Lesson 10
On or Off the Line?
10.1: Which One Doesn’t Belong: Lines in the Plane (5 minutes)
Warm-up
The purpose of this warm-up is to elicit ways students can describe different characteristics that arise when more than one line is graphed in a coordinate plane.
Launch
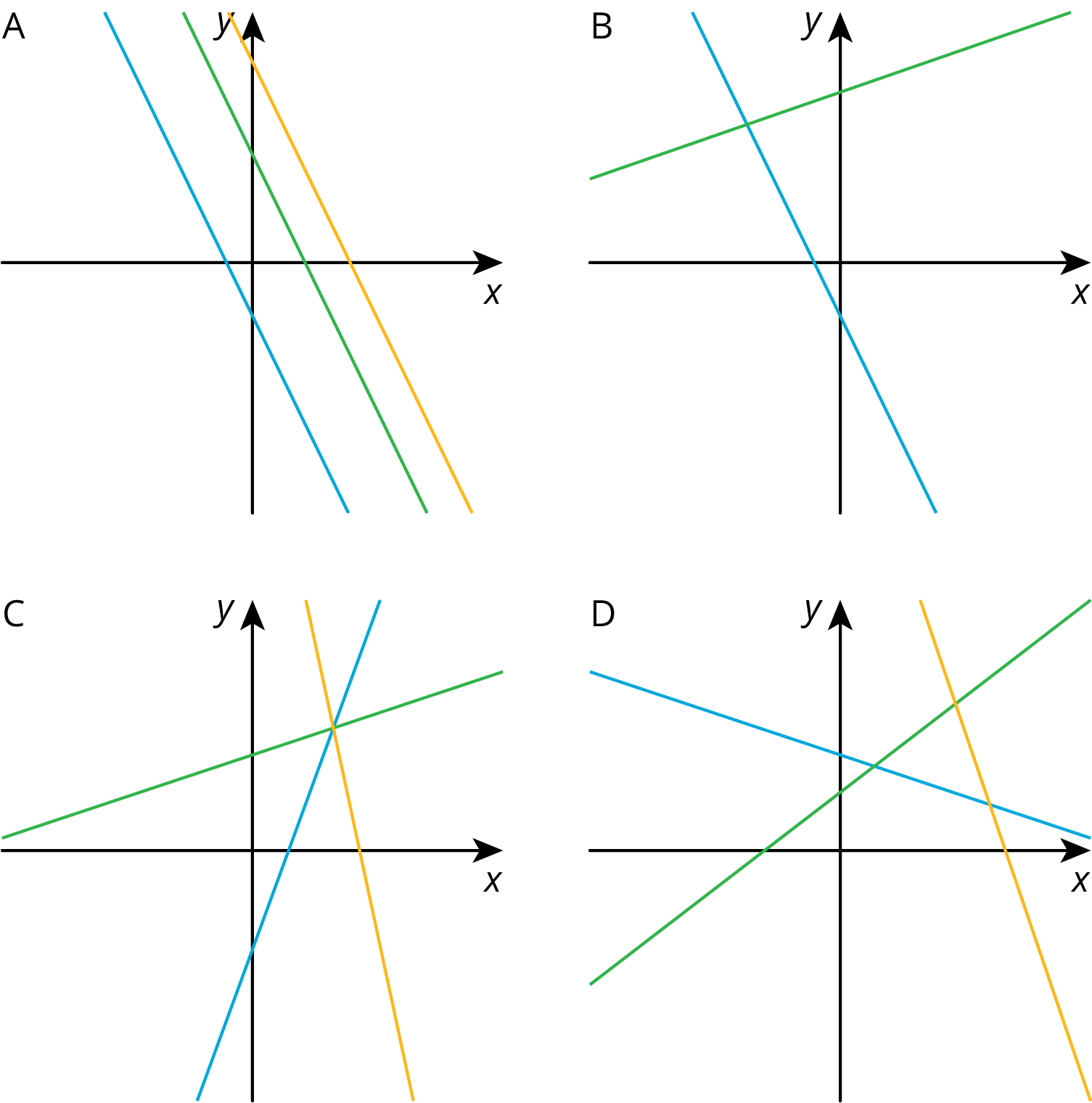
Arrange students in groups of 2–4. Display the image of all four graphs for all to see. Give students 1 minute of quiet think time and then time to share their thinking with their group. After everyone has conferred in groups, ask the groups to offer at least one reason why each graph doesn’t belong.
Student Facing
Which one doesn’t belong? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
After students have conferred in groups, invite each group to share one reason why a particular graph might not belong. Record and display the responses for all to see. After each response, ask the rest of the class if they agree or disagree. Since there is no single correct answer to the question of which graph does not belong, attend to students’ explanations and ensure the reasons given are correct. Encourage students to use concepts and language introduced in previous lessons about lines such as slope and intercepts. In particular, draw students’ attention to any intersections of the lines.
10.2: Pocket Full of Change (15 minutes)
Activity
In previous lessons, students have set two expressions equal to one another to find a common value where both expressions are true (if it exists). A system of two equations asks a similar question: at what common pair of values are both equations true? In this activity, students focus on a context involving coins and use multiple representations to think about the context in different ways. The goal of this activity is not for students to write equations or learn the language “system of equations,” but rather investigate the mathematical structure with two stated facts using familiar representations and context while reasoning about what must be true.
Monitor for students using different representations, such as a graph, table, or words, as they solve the final problem to share during the whole-class discussion.
Launch
Before looking at the task, tell students, “I have $2 in my pocket. What might be in my pocket?” Students will likely guess that you have two $1 bills, but ask what else it might be. Some answers could be 8 quarters; 200 pennies; a $2 bill; or 20 nickels, 2 quarters, and 5 dimes.
Read the problem context together. Ensure students understand that we know that Jada has exactly $2 in her pocket, that she only has quarters and dimes, and that she has exactly 17 coins. Give 1–2 minutes for students to read and complete the first problem. Display the table for all to see and ask students for values to fill in the table.
Give students 5–7 minutes of quiet work time to finish the remaining problems followed by a whole-class discussion.
Student Facing
Jada told Noah that she has $2 worth of quarters and dimes in her pocket and 17 coins all together. She asked him to guess how many of each type of coin she has.
- Here is a table that shows some combinations of quarters and dimes that are worth $2. Complete the table.
number of quarters number of dimes 0 20 4 0 5 - Here is a graph of the relationship between the number of quarters and the number of dimes when there are a total of 17 coins.
- What does Point \(A\) represent?
- How much money, in dollars, is the combination represented by Point \(A\) worth?

- Is it possible for Jada to have 4 quarters and 13 dimes in her pocket? Explain how you know.
- How many quarters and dimes must Jada have? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may be confused about the last row of the table. Tell them they can enter any values that make sense in the context and are not already on the table.
Activity Synthesis
The goal of this discussion is to focus students on what must be true based on the two facts they know: that the coins total $2 and that there are 17 coins. Begin the discussion by asking students about some things they know cannot be true about the coins in Jada’s pocket and how they know. Students may respond that Jada cannot have 20 dimes and 0 quarters because that is not 17 coins or other variations where either the coins do not total $2, there are not exactly 17 coins, or neither are true.
Select previously identified students to share how they answered the last problem. If possible, begin a sequence with a student who added on to the table representation to figure out the solution, followed by one who added onto the graph. Include any students who wrote out their reasoning in words last. After each student shares, connect to the idea that their solution is one where both facts are true.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Design Principle(s): Optimize output; Cultivate conversation
10.3: Making Signs (10 minutes)
Activity
In the previous activity, the system of equations was represented in words, a table, and a graph. In this activity, the system of equations is partially given in words, but key elements are only provided in the graph. Students have worked with lines that represent a context before. Now they must work with two lines at the same time to determine whether a point lies on one line, both lines, or neither line.
Launch
Arrange students in groups of 2. Give students 1 minute to read the problem and answer any questions they have about the context. Tell students to complete the table one row at a time with one person responding for Clare and the other responding for Andre. Give students 2–3 minutes to finish the table followed by whole-class discussion.
Supports accessibility for: Organization; Attention
Design Principle(s): Cultivate conversation; Maximize meta-awareness
Student Facing
Clare and Andre are making signs for all the lockers as part of the decorations for the upcoming spirit week. Yesterday, Andre made 15 signs and Clare made 5 signs. Today, they need to make more signs. Each person's progress today is shown in the coordinate plane.
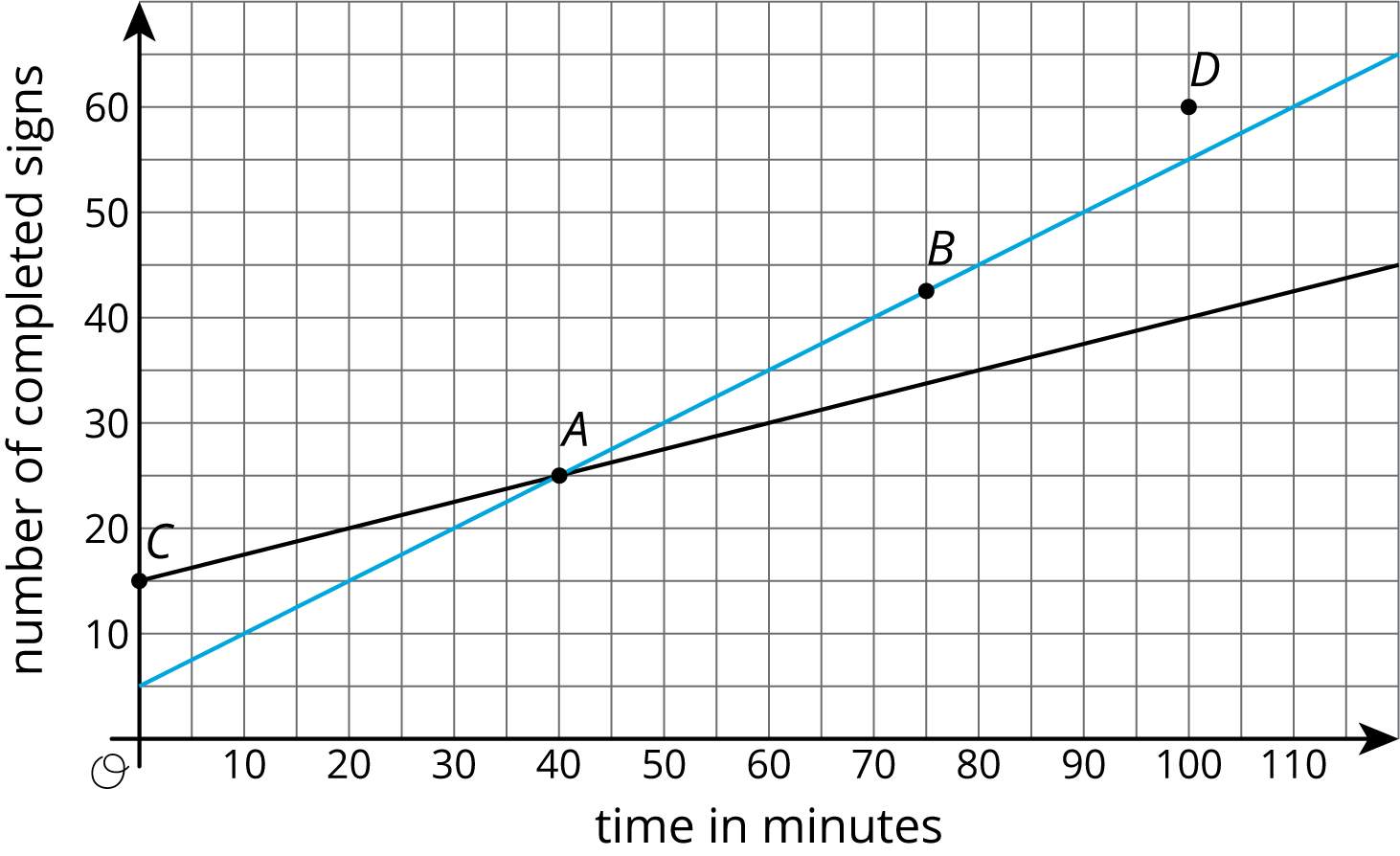
Based on the lines, mark the statements as true or false for each person.
| point | what it says | Clare | Andre |
|---|---|---|---|
| \(A\) | At 40 minutes, I have 25 signs completed. | ||
| \(B\) | At 75 minutes, I have 42 and a half signs completed. | ||
| \(C\) | At 0 minutes, I have 15 signs completed. | ||
| \(D\) | At 100 minutes, I have 60 signs completed. |
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
- 4 toothpicks make 1 square
- 7 toothpicks make 2 squares
- 10 toothpicks make 3 squares

Do you see a pattern? If so, how many toothpicks would you need to make 10 squares according to your pattern? Can you represent your pattern with an expression?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Display the graphs from the task statement. The goal of this discussion is for students to realize that points that lie on one line can be interpreted as statements that are true for Clare, and points that lie on the other line as statements that are true for Andre. Ask students:
- “What is true for Clare and Andre after 20 minutes?” (Clare has 15 signs completed and Andre has 20 signs completed.)
- “What, then, do you know about the point \((20, 15)\) and the equation for Clare's graph?” (The point \((20, 15)\) is a solution to the equation for Clare's graph.)
- “What do you know about the point \((20, 20)\) and the equation for Andre's graph?” (The point \((20, 20)\) is a solution to the equation for Andre's graph.)
Invite groups to share their reasoning about points A–D. Conclude by pointing out to students that, in this context, there are many points true for Clare and many points true for Andre but only one point true for both of them. Future lessons will be about how to figure out that point.
Lesson Synthesis
Lesson Synthesis
Tell students to think about how they found the ordered pair that makes two relationships true using tables and graphs today. Ask:
- “What are some advantages of tables? If you used two tables to describe the two relationships, how would you know whether a common point exists? If it did exist, how would you find it?” (Tables are good for knowing the exact values for individual points. If the common point is listed in each table, it may be easy to notice, but it may be missing from at least one table or difficult to find if the tables are large and unordered. If the common point is listed in each table, one row of the table should match in both columns.)
- “What are some advantages of graphs?” (Graphs give a better overall picture of the relationships and usually makes estimating (if not finding exactly) the common point easier.)
- “When using graphs, where are the points whose coordinates do not make a given relationship true? Do the coordinates of those points show up in a table of values?” (Points that are off of the line do not make the given relationship true. They can be above or below the line. The coordinates of these points do not show up in a table representing the given relationship.)
If time allows, invite students to make up their own stories with two quantities and two relationships to swap with a partner. Have each partner create either two tables of values, two graphs, or one of each to describe the situation and answer a question about the values of the two quantities that make both relationships true.
10.4: Cool-down - Another Pocket Full of Change (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We studied linear relationships in an earlier unit. We learned that values of \(x\) and \(y\) that make an equation true correspond to points \((x,y)\) on the graph. For example, if we have \(x\) pounds of flour that costs \$0.80 per pound and \(y\) pounds of sugar that costs \$0.50 per pound, and the total cost is \$9.00, then we can write an equation like this to represent the relationship between \(x\) and \(y:\)
\(\displaystyle 0.8x + 0.5y = 9\)
Since 5 pounds of flour costs \$4.00 and 10 pounds of sugar costs \$5.00, we know that \(x = 5\), \(y = 10\) is a solution to the equation, and the point \((5, 10)\) is a point on the graph. The line shown is the graph of the equation:
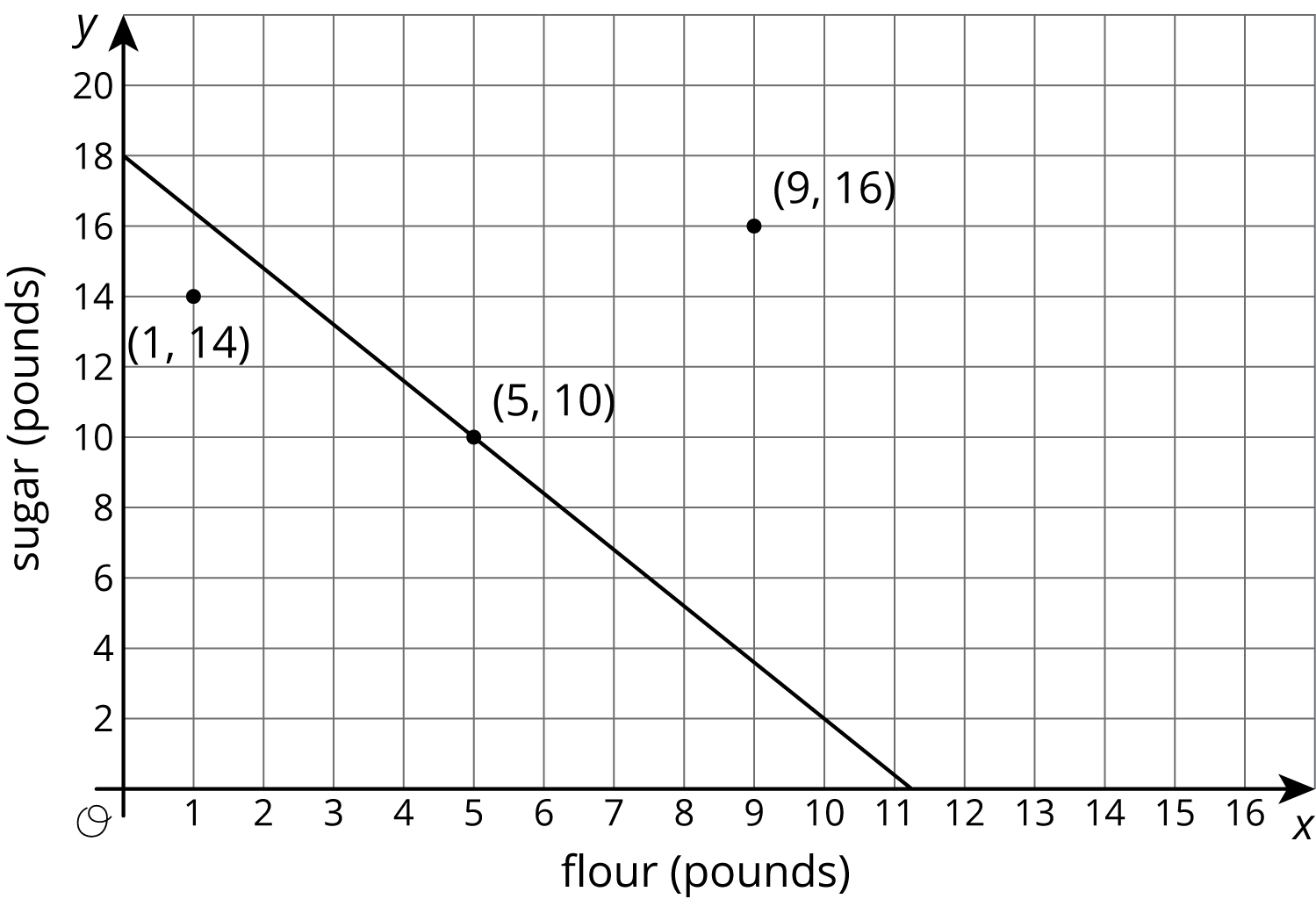
Notice that there are two points shown that are not on the line. What do they mean in the context? The point \((1,14)\) means that there is 1 pound of flour and 14 pounds of sugar. The total cost for this is \(0.8 \boldcdot 1 + 0.5 \boldcdot 14\) or \$7.80. Since the cost is not \$9.00, this point is not on the graph. Likewise, 9 pounds of flour and 16 pounds of sugar costs \(0.8 \boldcdot 9 + 0.5 \boldcdot 16\) or \$15.20, so the other point is not on the graph either.
Suppose we also know that the flour and sugar together weigh 15 pounds. That means that
\(\displaystyle x + y = 15\)
If we draw the graph of this equation on the same coordinate plane, we see it passes through two of the three labeled points:
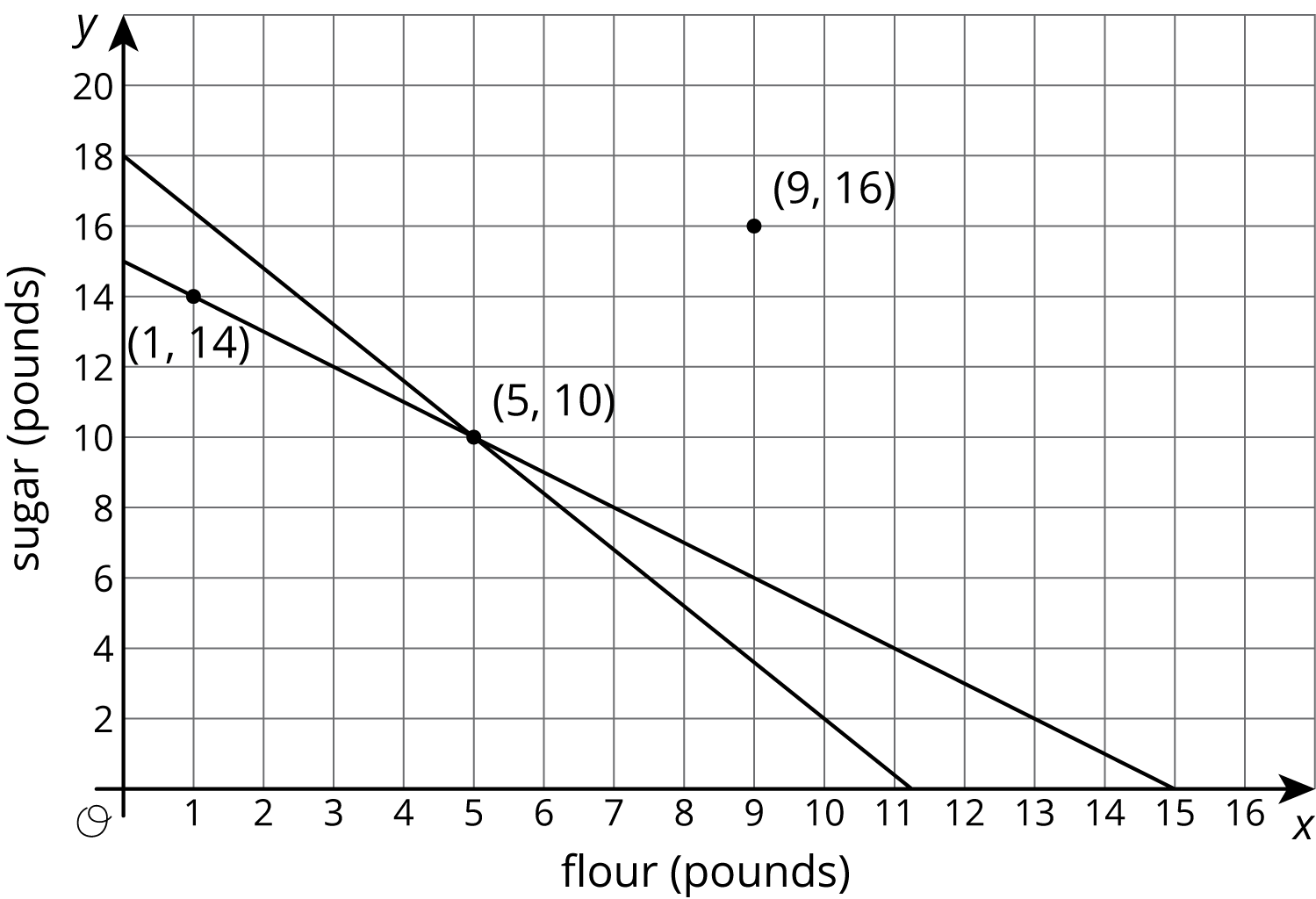
The point \((1,14)\) is on the graph of \(x+y=15\) because \(1 + 14 = 15\). Similarly, \(5 + 10 = 15\). But \(9 + 16 \neq 15\), so \((9, 16)\) is not on the graph of \(x+y = 15\). In general, if we have two lines in the coordinate plane,
- The coordinates of a point that is on both lines makes both equations true.
- The coordinates of a point on only one line makes only one equation true.
- The coordinates of a point on neither line make both equations false.