Lesson 13

Solving Systems of Equations

13.1: True or False: Two Lines (5 minutes)

The purpose of this warm-up is to get students to reason about solutions to equations by looking at their structure and reading their graphs. While some students may solve each equation to find if it is true or false without relating it to the graphs, encourage all students to show why their answer is correct based on the graphs of the equations during the whole-class discussion.

Arrange students in groups of 2. Display the image for all to see. Give students 2 minutes of quiet work time to begin the task individually and then 1 minute to discuss their responses with a partner followed by a whole-class discussion.

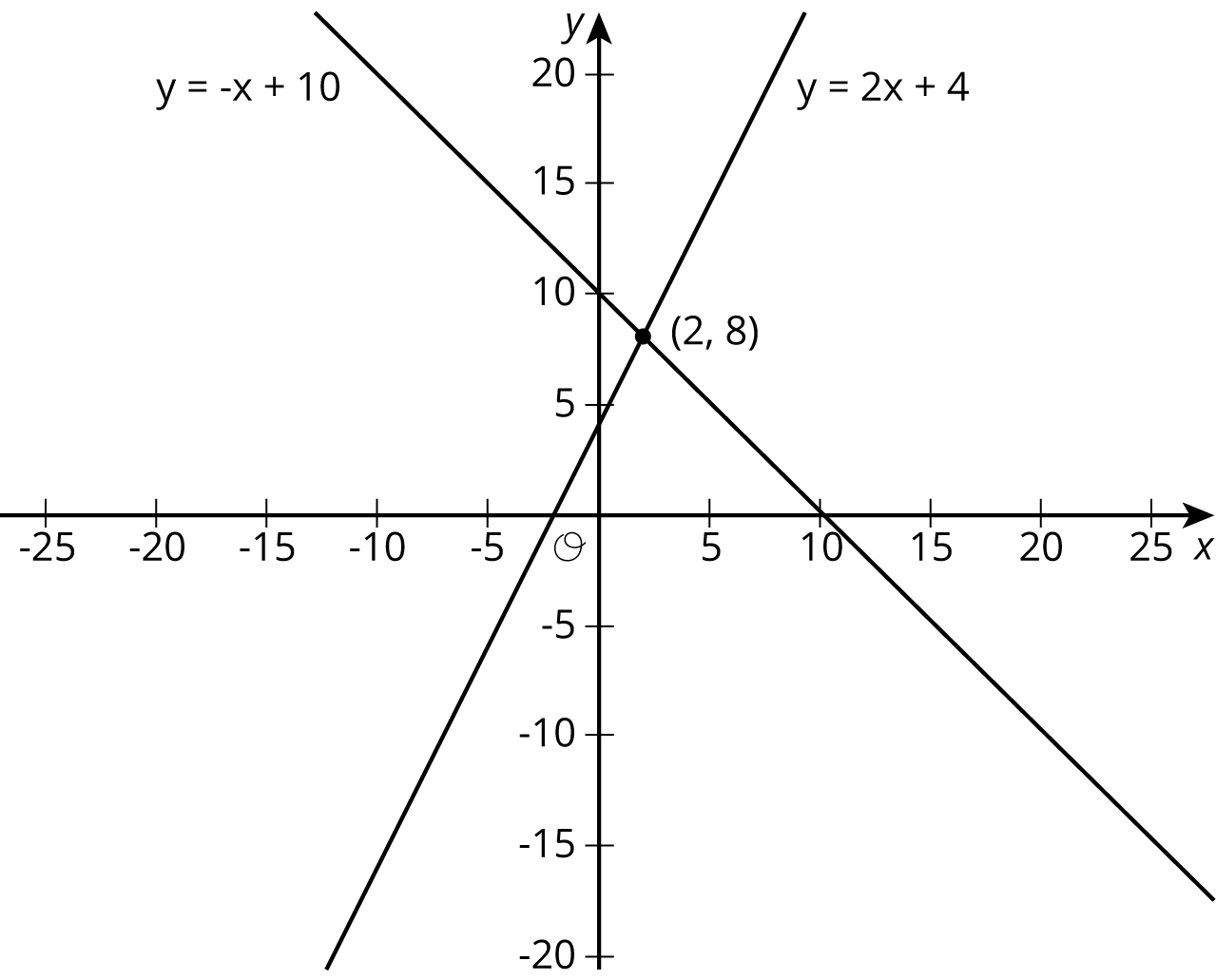
Use the lines to decide whether each statement is true or false. Be prepared to explain your reasoning using the lines.

A solution to \(8=\text-x+10\) is 2.
A solution to \(2=2x+4\) is 8.
A solution to \(\text-x+10=2x+4\) is 8.
A solution to \(\text-x+10=2x+4\) is 2.
There are no values of \(x\) and \(y\) that make \(y=\text-x+10\) and \(y=2x+4\) true at the same time.

For access, consult one of our IM Certified Partners.

Display the task image for all to see. Ask students to share their solutions and to reference the lines in their explanations. Emphasize the transitive property when students explain that since \(y=8\) at the point of intersection of \(y = 2x + 4\) and \(y=\text- x+10\), then both \(2x + 4 = 8\) and \(\text- x + 10 = 8\) are true, which leads to \(\text- x + 10 = 2x + 4\). If students do not mention this idea, bring it to their attention.

Ask students to solve \(\text- x + 10 = 2x + 4\) for \(x\) if they’ve not already done so and confirm that \(x=2\) is the \(x\)-coordinate of the solution to the system of equations.

13.2: Matching Graphs to Systems (15 minutes)

This activity represents the first time students solve a system of equations using algebraic methods. They first match systems of equations to their graphs and then calculate the solutions to each system. The purpose of matching is so students have a way to check that their algebraic solutions are correct, but not to shortcut the algebraic process since the graphs themselves do not include enough detail to accurately guess the coordinates of the solution.

Digital

Keep students in groups of 2. Give 2–3 minutes of quiet work time for the first problem and then ask students to pause their work. Select 1–2 students per figure to explain how they matched it to one of the systems of equations. For example, a student may identify the system matching Figure A as the only system with an equation that has negative slope. Give students 5–7 minutes of work time with their partner to complete the activity followed by a whole-class discussion. If students finish early and have not already done so on their own, ask them how they could check their solutions and encourage them to do so.

If using the digital activity, implement the lesson as indicated above. The only difference between the print and digital version is the digital lesson has an applet that will simulate the graphs so the students have another way of checking their solutions.

Representation: Internalize Comprehension. Demonstrate and encourage students to use color coding and annotations to highlight connections between representations in a problem. Invite students to illustrate connections between slopes and \(y\)-intercepts of each line to the corresponding parts of each equation using the same color.
Supports accessibility for: Visual-spatial processing

Conversing: MLR8 Discussion Supports. Use this routine to support small-group discussion as students describe the reasons for their matches. Arrange students in groups of 2. Invite Partner A to begin with this sentence frame: “Figure ____ matches with the system of equations ____, because ____.” Invite the listener, Partner B, to press for additional details referring to specific features of the graphs (e.g. positive slope, negative y-intercept, coordinates of the intersection point, etc). Students should switch roles for each figure. This will help students justify how features of the graph can be used to identify matching equations.
Design Principle(s): Support sense-making; Cultivate conversation

Here are three systems of equations graphed on a coordinate plane:

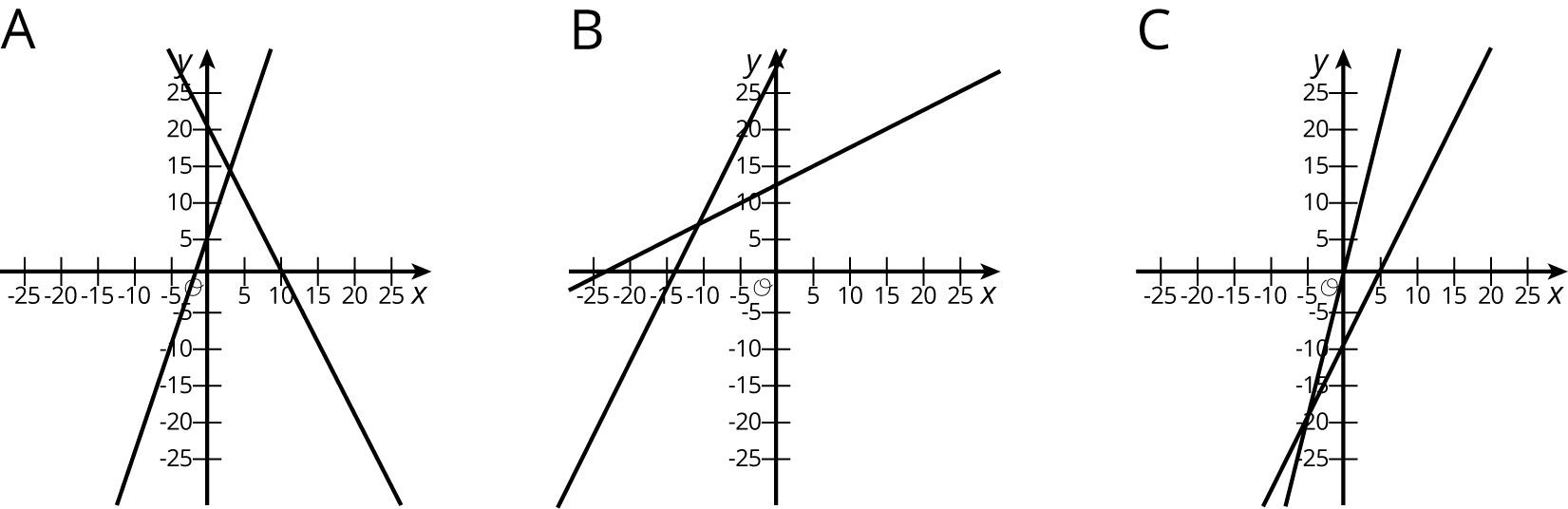
Three graphs, with two lines each, in the x y plane.

Match each figure to one of the systems of equations shown here.
1. \(\begin{cases} y=3x+5\\ y=\text- 2x+20 \end{cases}\)
2. \(\begin{cases} y=2x-10\\ y=4x-1 \end{cases}\)
3. \(\begin{cases} y=0.5x+12\\ y=2x+27 \end{cases}\)
Find the solution to each system and then check that your solution is reasonable on the graph.
- Notice that the sliders set the values of the coefficient and the constant term in each equation.
- Change the sliders to the values of the coefficient and the constant term in the next pair of equations.
- Click on the spot where the lines intersect and a labeled point should appear.

For access, consult one of our IM Certified Partners.

Here are three systems of equations graphed on a coordinate plane:

Match each figure to one of the systems of equations shown here.
1. \(\begin{cases} y=3x+5\\ y=\text-2x+20 \end{cases}\)
2. \(\begin{cases} y=2x-10\\ y=4x-1 \end{cases}\)
3. \(\begin{cases} y=0.5x+12\\ y=2x+27 \end{cases}\)
Find the solution to each system and check that your solution is reasonable based on the graph.

For access, consult one of our IM Certified Partners.

The goal of this discussion is to deliberately connect the current topic of systems of equations to the previous topic of solving equations with variables on both sides. For each of the following questions, give students 30 seconds of quiet think time and then invite students per question to explain their answer. The final question looks ahead to the following activity.

“Do you need to see the graphs of the equations in a system in order to solve the system?" (No, but the graphs made me feel more confident that my answer was correct.)
“How do you know your solution doesn’t contain any errors?" (I know my solution does not have errors because I substituted my values for \(x\) and \(y\) into the equations and they made both equations true.)
“How does solving systems of equations compare to solving equations with variables on both sides like we did in earlier lessons?" (They are very similar, only with a system of equations you are finding an \(x\) and a \(y\) to make both equations true and not just an \(x\) to make one equation true.)
“When you solved equations with variables on both sides, some had one solution, some had no solutions, and some had infinite solutions. Do you think systems of equations can have no solutions or infinite solutions?" (Yes. We have seen some graphs of parallel lines where there were no solutions and some graphs of lines that are on top of one another where there are infinite solutions.)

13.3: Different Types of Systems (15 minutes)

While students have encountered equations with different numbers of solutions in earlier activities, this is the first activity where students connect systems of equations with their previous thinking about equations that have no solution, one solution, or infinitely many solutions. The purpose of this activity is for students to connect the features of the graph of the equations of a system to the number of solutions of a system (MP7). While students are not asked to solve the systems of equations, they may choose to rewrite the equations in equivalent forms as they work to graph the lines.

Depending on instructional time available, you may wish to alter the activity and ask students to solve one or more of the systems of equations algebraically.

Digital

Remind students of the activity they did sorting equations with a single variable where each equation had either one solution, no solution, or infinitely many solutions. Tell them that, just like one variable equations, systems of equations can also have either one solution, no solution, or infinitely many solutions. Point out that in the previous activity, each of the three systems of equations had one solution, which they found algebraically by solving the system, and so the graphs of the equations of the system showed one point where the lines intersected. Ask students what they think the graphs of equations from systems with no or infinitely many solutions might look like. Allow 30 seconds of quiet think time before inviting a few students to suggest possibilities for each type of system while recording and displaying their ideas for all to see. Remind students of the activities in previous lessons where they have seen these situations and their graphs (a bike race between Elena and Jada had infinite solutions and stacking different sized cups had none).

Arrange students in groups of 2–3. Provide each group with access to straightedges and scissors as well as one copy of the blackline master. Encourage partners to split the work by cutting apart the problems, each taking one to three graphs, and then trading pages within their group to check the work. Give 4–6 minutes for groups to complete the graphs and remind students to use straightedges for precision while graphing.

Before beginning the final problem, have each group trade their work with another group and place a question mark next to the graphs they are not sure are correct. Give groups 3–4 minutes to revise as needed and write their descriptions for the second problem followed by a whole-class discussion.

If using the digital activity, use the discussion structure above. The digital applet will make the graphing and solving of systems go quickly so students can spend more time analyzing the solutions. Using technology to graph allows students to focus on the main purpose of the lesson and also recognize the value in technology when solving systems in addition to appreciating when the graphing method is efficient. In this activity, one of the main purposes is to notice what is common among systems with the same number of solutions. Therefore, it may be useful to ask students to justify why the lines graphed with no obvious intersections are actually parallel.

Your teacher will give you a page with 6 systems of equations.

Graph each system of equations by typing each pair of the equations in the applet, one at a time.
Describe what the graph of a system of equations looks like when it has . . .
1. 1 solution
2. 0 solutions
3. infinitely many solutions

Use the applet to confirm your answer to question 2.

For access, consult one of our IM Certified Partners.

Your teacher will give you a page with some systems of equations.

Graph each system of equations carefully on the provided coordinate plane.
Describe what the graph of a system of equations looks like when it has . . .
1. 1 solution
2. 0 solutions
3. infinitely many solutions

For access, consult one of our IM Certified Partners.

Are you ready for more?

The graphs of the equations \(Ax + By = 15\) and \(Ax - By = 9\) intersect at \((2,1)\). Find \(A\) and \(B\). Show or explain your reasoning.

For access, consult one of our IM Certified Partners.

The goal of this discussion is for students to draw conclusions about the relationship between the number of solutions a system of equations has and the appearance of the graphs of the equations in the system. Select 2–3 students to share and explain their answers to the second problem.

If no students mention it, bring in slope language and how inspecting the slopes of the equations before graphing or solving can give clues to the possible number of solutions the system has. In particular, students should notice that systems with lines that have different slopes have a single solution, lines that have the same slope and different \(y\)-intercept have no solution, and lines that have the same slope and \(y\)-intercept will have infinitely many solutions.

Assign a number of solutions (one, none, or infinite) to each group and ask them to write a system of equations that would have that number of solutions. Have a few groups share their systems and describe how the graphs of the systems would look. In particular, ask each group to describe how the slope and \(y\)-intercept of their written lines would be seen in the graph and how the number of solutions would appear on the graph. Following the description, display the graph of the system using a digital resource, if possible, or a general sketch on a set of displayed axes.

Writing: MLR1 Stronger and Clearer Each Time. Use this routine to give students an opportunity to revise and improve their response to the final question, “Describe what the graph of a system of equations looks like when it has one solution, zero solutions, and infinitely many solutions.” Give students time to meet with 2–3 partners, to share and get feedback on their response. Encourage the listener to press for supporting details and evidence by asking, “How do the slopes compare?”, “How do the \(y\)-intercepts compare?” or “What do you notice about the slopes and the \(y\)-intercepts?” Students can borrow ideas and language from each partner to strengthen the final product. This will help students produce a written generalization for how to identify the number of solutions for a system of equations by using the features of a graph.
Design Principle(s): Optimize output (for generalization)

Lesson Synthesis

To highlight the connection between the number of solutions to a system of equations and features of its graph and equations, ask:

“How can you know the number of solutions for a system of equations from its graph?” (If the two lines intersect at a point, there is one solution. If the two lines are parallel and do not intersect, there are no solutions. If the two lines are drawn through the same points, there are infinitely many solutions.)
“How can you know the number of solutions for a system of equations from their equations?” (If the two equations have different slopes, there is one solution. If the two equations have the same slope and different \(y\)-intercepts, there are no solutions. If the two equations have the same slope and the same \(y\)-intercept, there are infinitely many solutions.)

If students do not make the connection themselves, remind them of their earlier conclusions about the number of solutions and equation in one variable has.

13.4: Cool-down - Two Lines (5 minutes)

For access, consult one of our IM Certified Partners.

Student Lesson Summary

Sometimes it is easier to solve a system of equations without having to graph the equations and look for an intersection point. In general, whenever we are solving a system of equations written as

\(\displaystyle \begin{cases} y = \text{[some stuff]}\\ y = \text{[some other stuff]} \end{cases}\)

we know that we are looking for a pair of values \((x,y)\) that makes both equations true. In particular, we know that the value for \(y\) will be the same in both equations. That means that

\(\displaystyle \text{[some stuff]} = \text{[some other stuff]}\)

For example, look at this system of equations:

\(\displaystyle \begin{cases} y = 2x + 6 \\ y = \text-3x - 4 \end{cases}\)

Since the \(y\) value of the solution is the same in both equations, then we know \(\displaystyle 2x + 6 = \text-3x -4\)

We can solve this equation for \(x\):

\(\begin{align} 2x+6 &= \text-3x-4&& \\ 5x+6 &=\text-4\ &&\text{add \(3x\) to each side}\\ 5x &=\text-10\ &&\text{subtract 6 from each side}\\ x &=\text-2\ &&\text{divide each side by 5}\ \end{align}\)

But this is only half of what we are looking for: we know the value for \(x\), but we need the corresponding value for \(y\). Since both equations have the same \(y\) value, we can use either equation to find the \(y\)-value:

\(\displaystyle y = 2(\text-2) + 6\)

\(\displaystyle y = \text-3(\text-2) -4\)

In both cases, we find that \(y = 2\). So the solution to the system is \((\text-2,2)\). We can verify this by graphing both equations in the coordinate plane.

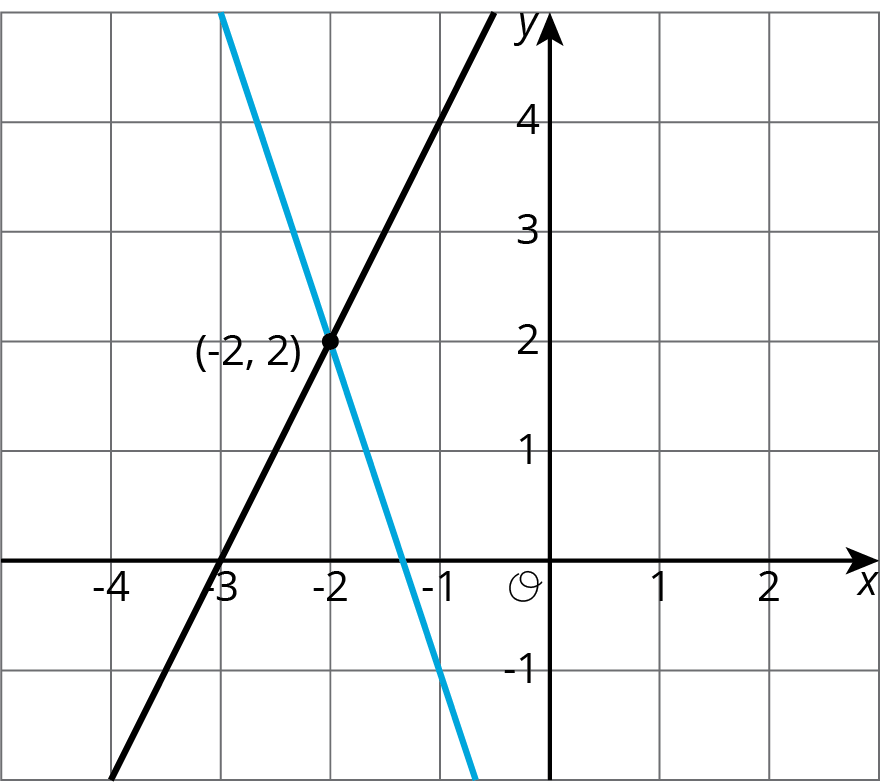
In general, a system of linear equations can have:

No solutions. In this case, the lines that correspond to each equation never intersect.
Exactly one solution. The lines that correspond to each equation intersect in exactly one point.
An infinite number of solutions. The graphs of the two equations are the same line!

Lesson 13

13.1: True or False: Two Lines (5 minutes)

Warm-up

Launch

Student Facing

Student Response

Activity Synthesis

13.2: Matching Graphs to Systems (15 minutes)

Activity

Launch

Student Facing

Student Response

Launch

Student Facing

Student Response

Activity Synthesis

13.3: Different Types of Systems (15 minutes)

Activity

Launch

Student Facing

Student Response

Launch

Student Facing

Student Response

Student Facing

Are you ready for more?

Student Response

Activity Synthesis

Lesson Synthesis

Lesson Synthesis

13.4: Cool-down - Two Lines (5 minutes)

Cool-Down

Student Lesson Summary

Student Facing