Lesson 2
Keeping the Equation Balanced
Problem 1
Which of the changes would keep the hanger in balance?
Select all that apply.
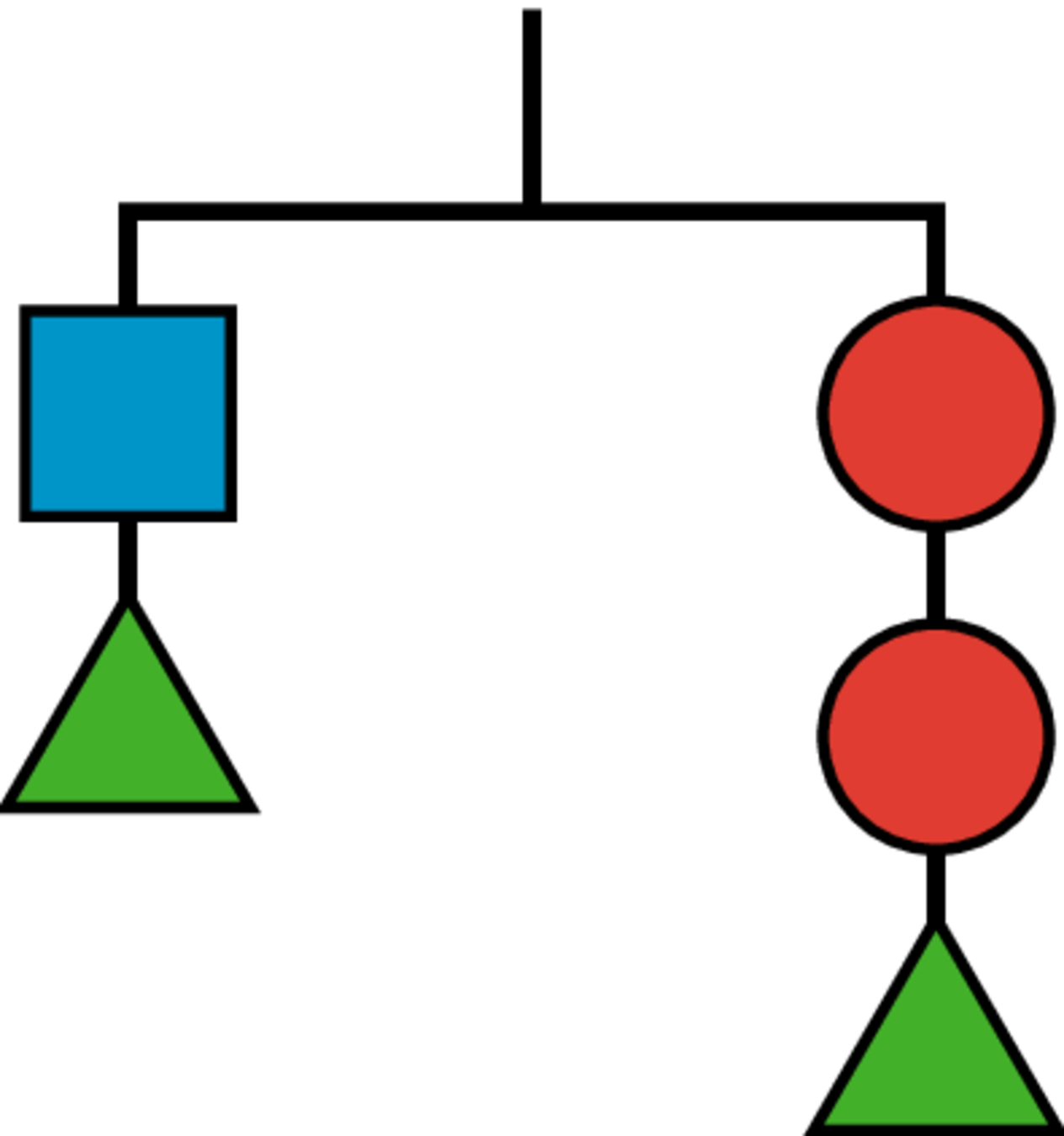
Adding two circles on the left and a square on the right
Adding 2 triangles to each side
Adding two circles on the right and a square on the left
Adding a circle on the left and a square on the right
Adding a triangle on the left and a square on the right
Solution
For access, consult one of our IM Certified Partners.
Problem 2
Here is a balanced hanger diagram.
Each triangle weighs 2.5 pounds, each circle weighs 3 pounds, and \(x\) represents the weight of each square. Select all equations that represent the hanger.

\(x+x+x+x+11=x+11.5\)
\(2x=0.5\)
\(4x+5+6=2x+2.5+6\)
\(2x+2.5=3\)
\(4x+2.5+2.5+3+3=2x+2.5+3+3+3\)
Solution
For access, consult one of our IM Certified Partners.
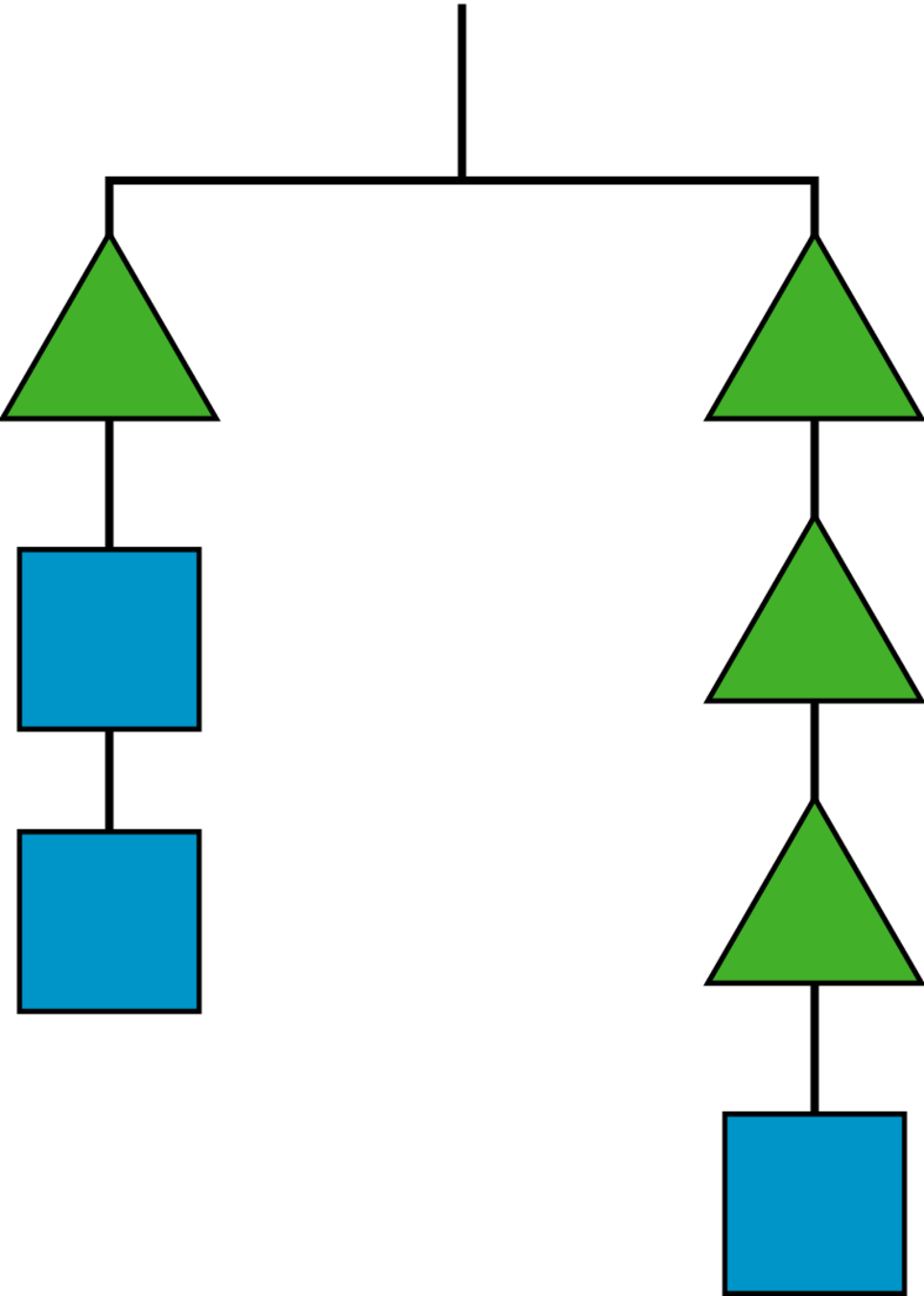
Problem 3
What is the weight of a square if a triangle weighs 4 grams?
Explain your reasoning.
Solution
For access, consult one of our IM Certified Partners.
Problem 4
Andre came up with the following puzzle. “I am three years younger than my brother, and I am 2 years older than my sister. My mom's age is one less than three times my brother's age. When you add all our ages, you get 87. What are our ages?”
-
Try to solve the puzzle.
-
Jada writes this equation for the sum of the ages: \((x)+(x+3)+(x-2) + 3(x+3) - 1=87\).
Explain the meaning of the variable and each term of the equation. -
Write the equation with fewer terms.
-
Solve the puzzle if you haven’t already.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 1.)Problem 5
These two lines are parallel. Write an equation for each.

Solution
For access, consult one of our IM Certified Partners.
(From Unit 3, Lesson 8.)