Lesson 10
On or Off the Line?
Let’s interpret the meaning of points in a coordinate plane.
10.1: Which One Doesn’t Belong: Lines in the Plane
Which one doesn’t belong? Explain your reasoning.
10.2: Pocket Full of Change
Jada told Noah that she has $2 worth of quarters and dimes in her pocket and 17 coins all together. She asked him to guess how many of each type of coin she has.
- Here is a table that shows some combinations of quarters and dimes that are worth $2. Complete the table.
number of quarters number of dimes 0 20 4 0 5 - Here is a graph of the relationship between the number of quarters and the number of dimes when there are a total of 17 coins.
- What does Point \(A\) represent?
- How much money, in dollars, is the combination represented by Point \(A\) worth?

- Is it possible for Jada to have 4 quarters and 13 dimes in her pocket? Explain how you know.
- How many quarters and dimes must Jada have? Explain your reasoning.
10.3: Making Signs
Clare and Andre are making signs for all the lockers as part of the decorations for the upcoming spirit week. Yesterday, Andre made 15 signs and Clare made 5 signs. Today, they need to make more signs. Each person's progress today is shown in the coordinate plane.
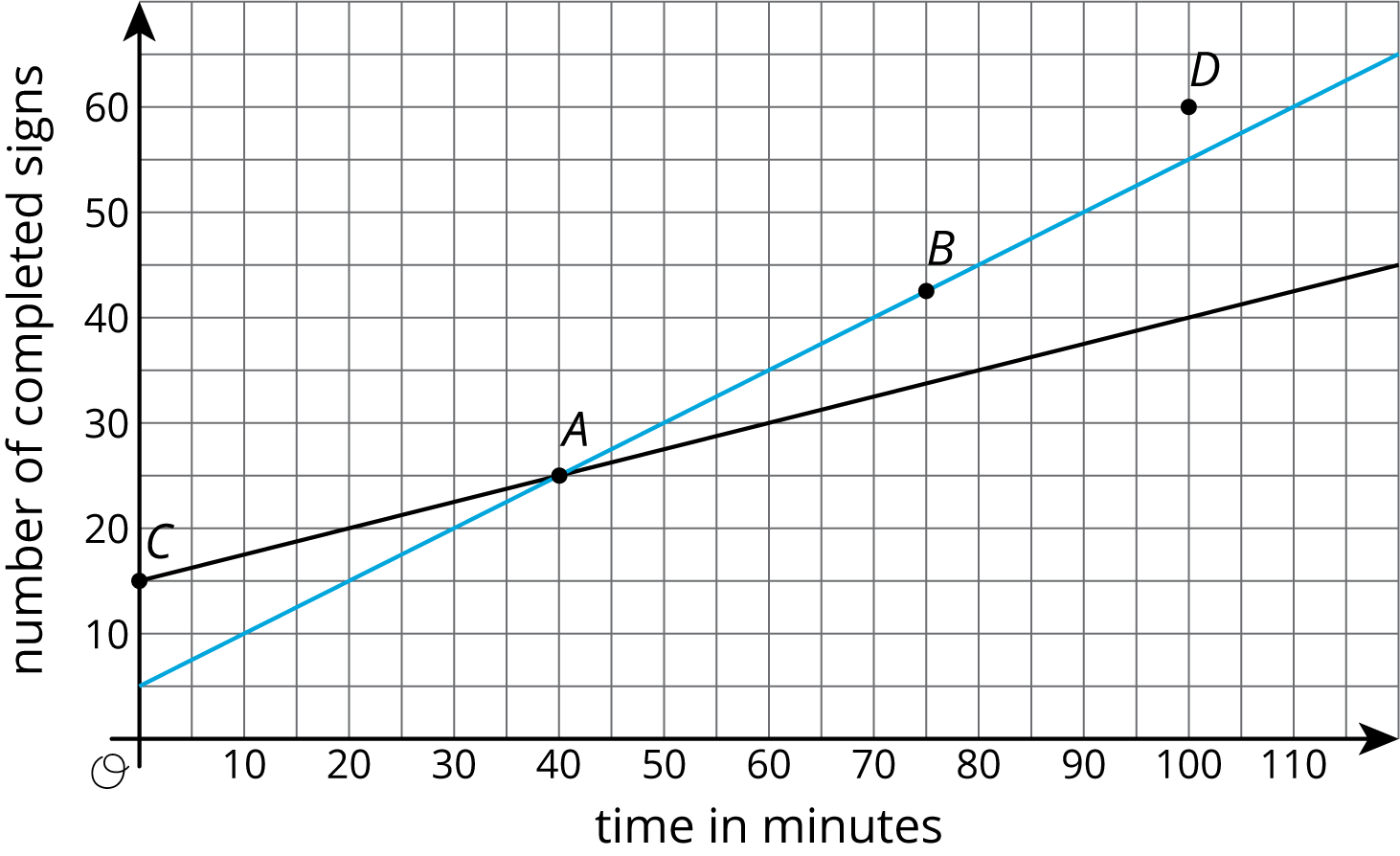
Based on the lines, mark the statements as true or false for each person.
| point | what it says | Clare | Andre |
|---|---|---|---|
| \(A\) | At 40 minutes, I have 25 signs completed. | ||
| \(B\) | At 75 minutes, I have 42 and a half signs completed. | ||
| \(C\) | At 0 minutes, I have 15 signs completed. | ||
| \(D\) | At 100 minutes, I have 60 signs completed. |
- 4 toothpicks make 1 square
- 7 toothpicks make 2 squares
- 10 toothpicks make 3 squares

Do you see a pattern? If so, how many toothpicks would you need to make 10 squares according to your pattern? Can you represent your pattern with an expression?
Summary
We studied linear relationships in an earlier unit. We learned that values of \(x\) and \(y\) that make an equation true correspond to points \((x,y)\) on the graph. For example, if we have \(x\) pounds of flour that costs \$0.80 per pound and \(y\) pounds of sugar that costs \$0.50 per pound, and the total cost is \$9.00, then we can write an equation like this to represent the relationship between \(x\) and \(y:\)
\(\displaystyle 0.8x + 0.5y = 9\)
Since 5 pounds of flour costs \$4.00 and 10 pounds of sugar costs \$5.00, we know that \(x = 5\), \(y = 10\) is a solution to the equation, and the point \((5, 10)\) is a point on the graph. The line shown is the graph of the equation:
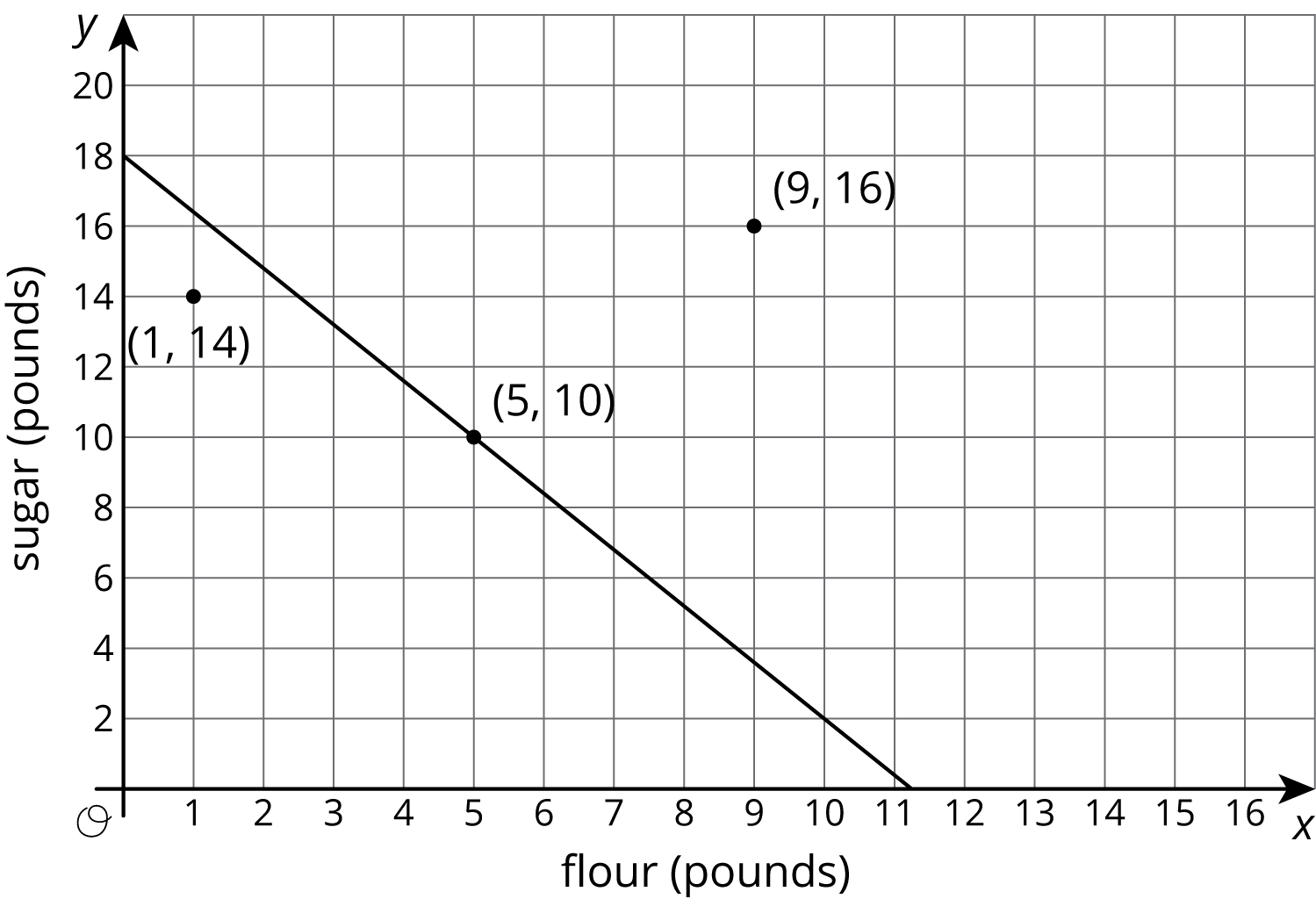
Notice that there are two points shown that are not on the line. What do they mean in the context? The point \((1,14)\) means that there is 1 pound of flour and 14 pounds of sugar. The total cost for this is \(0.8 \boldcdot 1 + 0.5 \boldcdot 14\) or \$7.80. Since the cost is not \$9.00, this point is not on the graph. Likewise, 9 pounds of flour and 16 pounds of sugar costs \(0.8 \boldcdot 9 + 0.5 \boldcdot 16\) or \$15.20, so the other point is not on the graph either.
Suppose we also know that the flour and sugar together weigh 15 pounds. That means that
\(\displaystyle x + y = 15\)
If we draw the graph of this equation on the same coordinate plane, we see it passes through two of the three labeled points:
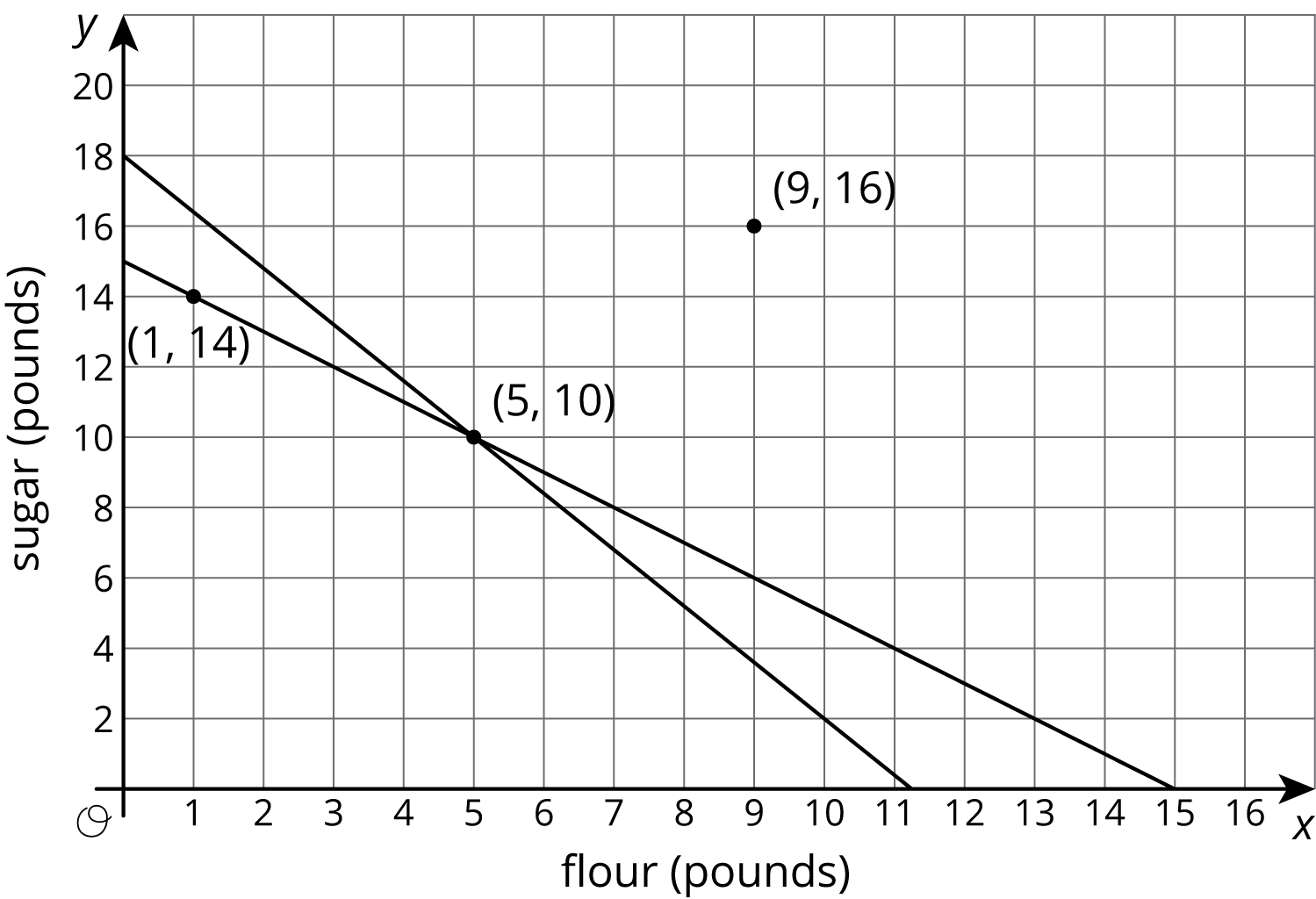
The point \((1,14)\) is on the graph of \(x+y=15\) because \(1 + 14 = 15\). Similarly, \(5 + 10 = 15\). But \(9 + 16 \neq 15\), so \((9, 16)\) is not on the graph of \(x+y = 15\). In general, if we have two lines in the coordinate plane,
- The coordinates of a point that is on both lines makes both equations true.
- The coordinates of a point on only one line makes only one equation true.
- The coordinates of a point on neither line make both equations false.