Lesson 9
Moves in Parallel
Lesson Narrative
The previous lesson examines the impact of rotations on line segments and polygons. This lesson focuses on the effects of rigid transformations on lines. In particular, students see that parallel lines are taken to parallel lines and that a \(180^\circ\) rotation about a point on the line takes the line to itself. In grade 7, students found that vertical angles have the same measure, and they justify that here using a \(180^\circ\) rotation.
As they investigate how \(180^\circ\) rotations influence parallel lines and intersecting lines, students are looking at specific examples but their conclusions hold for all pairs of parallel or intersecting lines. No special properties of the two intersecting lines are used so the \(180^\circ\) rotation will show that vertical angles have the same measure for any pair of vertical angles.
Learning Goals
Teacher Facing
- Comprehend that a rotation by 180 degrees about a point of two intersecting lines moves each angle to the angle that is vertical to it.
- Describe (orally and in writing) observations of lines and parallel lines under rigid transformations, including lines that are taken to lines and parallel lines that are taken to parallel lines.
- Draw and label rigid transformations of a line and explain the relationship between a line and its image under the transformation.
- Generalize (orally) that “vertical angles” are congruent using informal arguments about 180 degree rotations of lines.
Student Facing
Let’s transform some lines.
Required Materials
Learning Targets
Student Facing
- I can describe the effects of a rigid transformation on a pair of parallel lines.
- If I have a pair of vertical angles and know the angle measure of one of them, I can find the angle measure of the other.
Glossary Entries
-
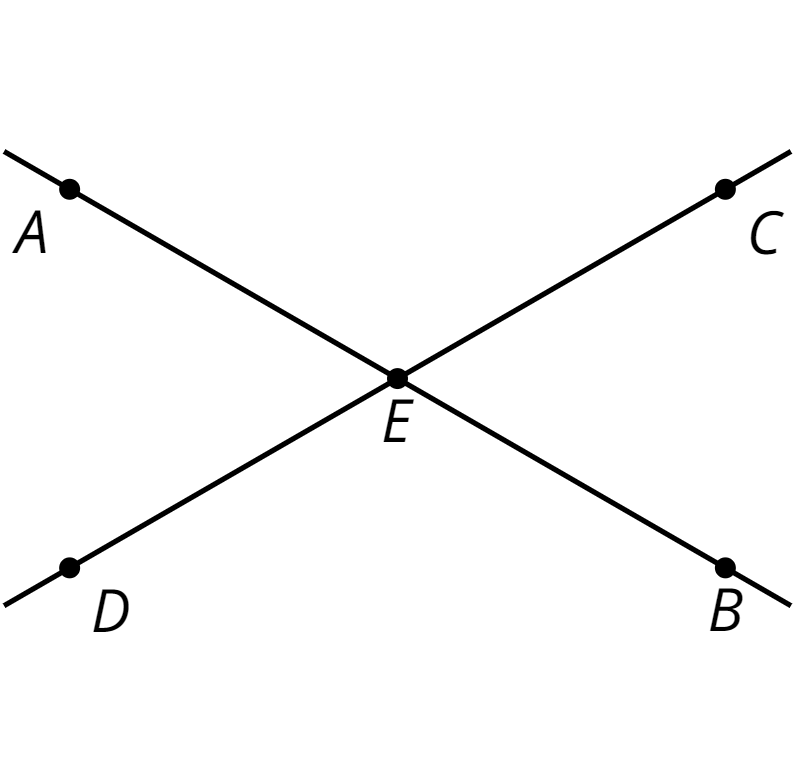
vertical angles
Vertical angles are opposite angles that share the same vertex. They are formed by a pair of intersecting lines. Their angle measures are equal.
For example, angles \(AEC\) and \(DEB\) are vertical angles. If angle \(AEC\) measures \(120^\circ\), then angle \(DEB\) must also measure \(120^\circ\).
Angles \(AED\) and \(BEC\) are another pair of vertical angles.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |