Lesson 7

No Bending or Stretching

View Student Lesson

Problem 1

Is there a rigid transformation taking Rhombus P to Rhombus Q? Explain how you know.

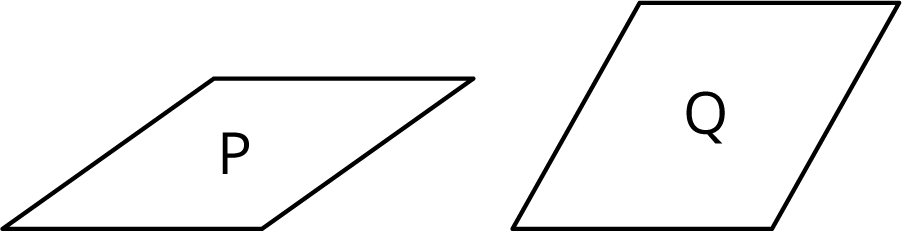
Two rhombi, rhombus P and rhombus Q. Rhombus P and Q appear to have the same length bases, but rhombus Q is taller and rhombus P sides have a lower slopes.

 

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Describe a rigid transformation that takes Triangle A to Triangle B.

Triangle A and its image triangle B on a coordinate plane, origin \(O\). 

 

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Is there a rigid transformation taking Rectangle A to Rectangle B? Explain how you know.

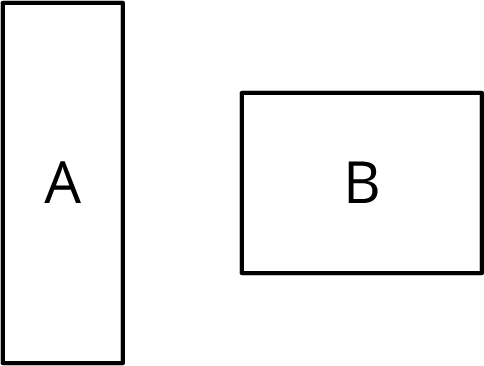
Two rectangles, A and B. Rectangle A is tall and thin, and the base is the smaller side. Rectangle B is wider and shorter than rectangle A, and the base is the longer side of B.

Solution

For access, consult one of our IM Certified Partners.

Problem 4

For each shape, draw its image after performing the transformation. If you get stuck, consider using tracing paper.

  1. Translate the shape so that \(A\) goes to \(A’\).
Quadrilateral A with point A on the lower left and point A prime on a triangular grid.
  1. Rotate the shape 180 degrees counterclockwise around \(B\).
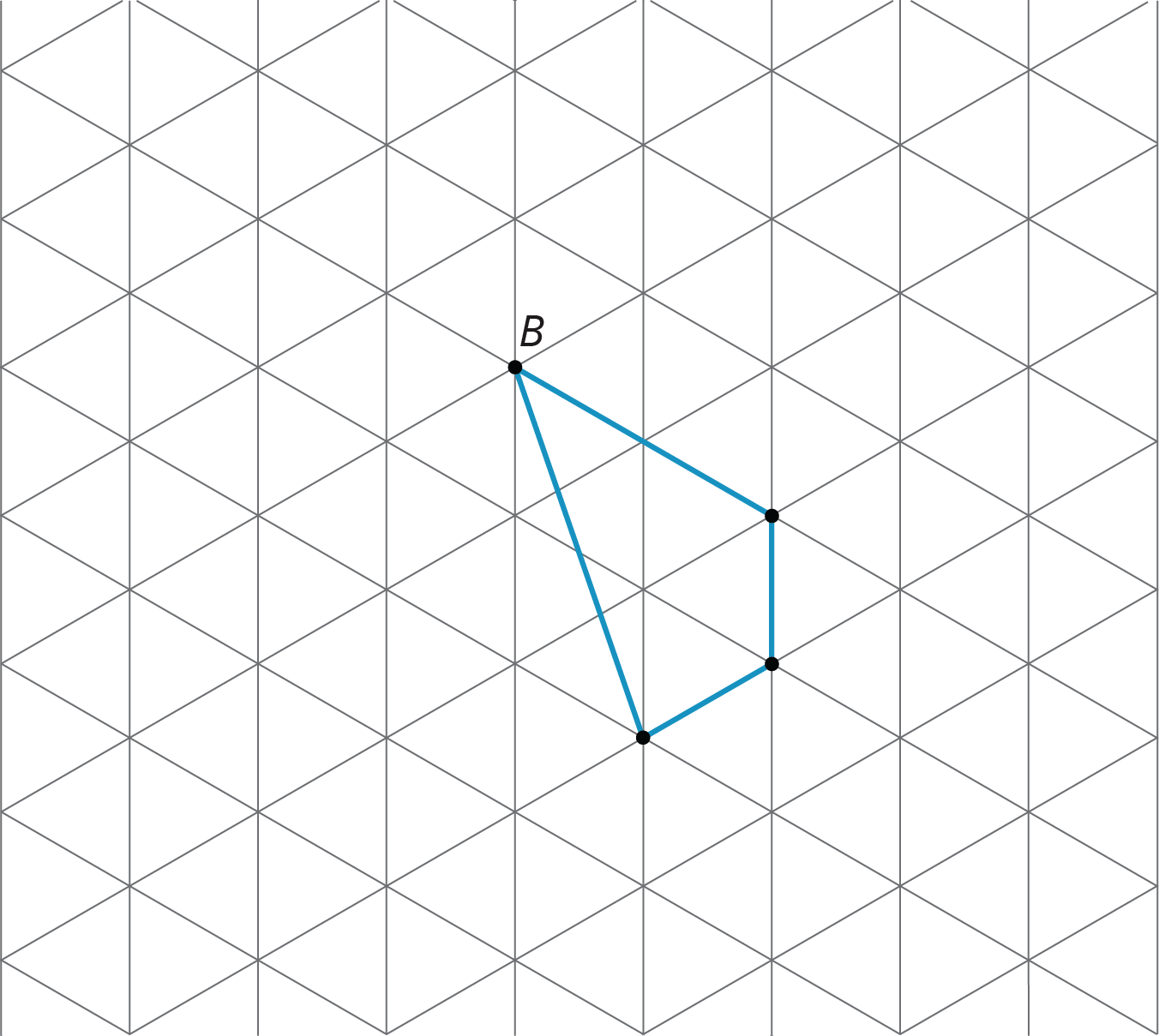
Quadrilateral B on a triangular grid.
  1. Reflect the shape over the line shown.
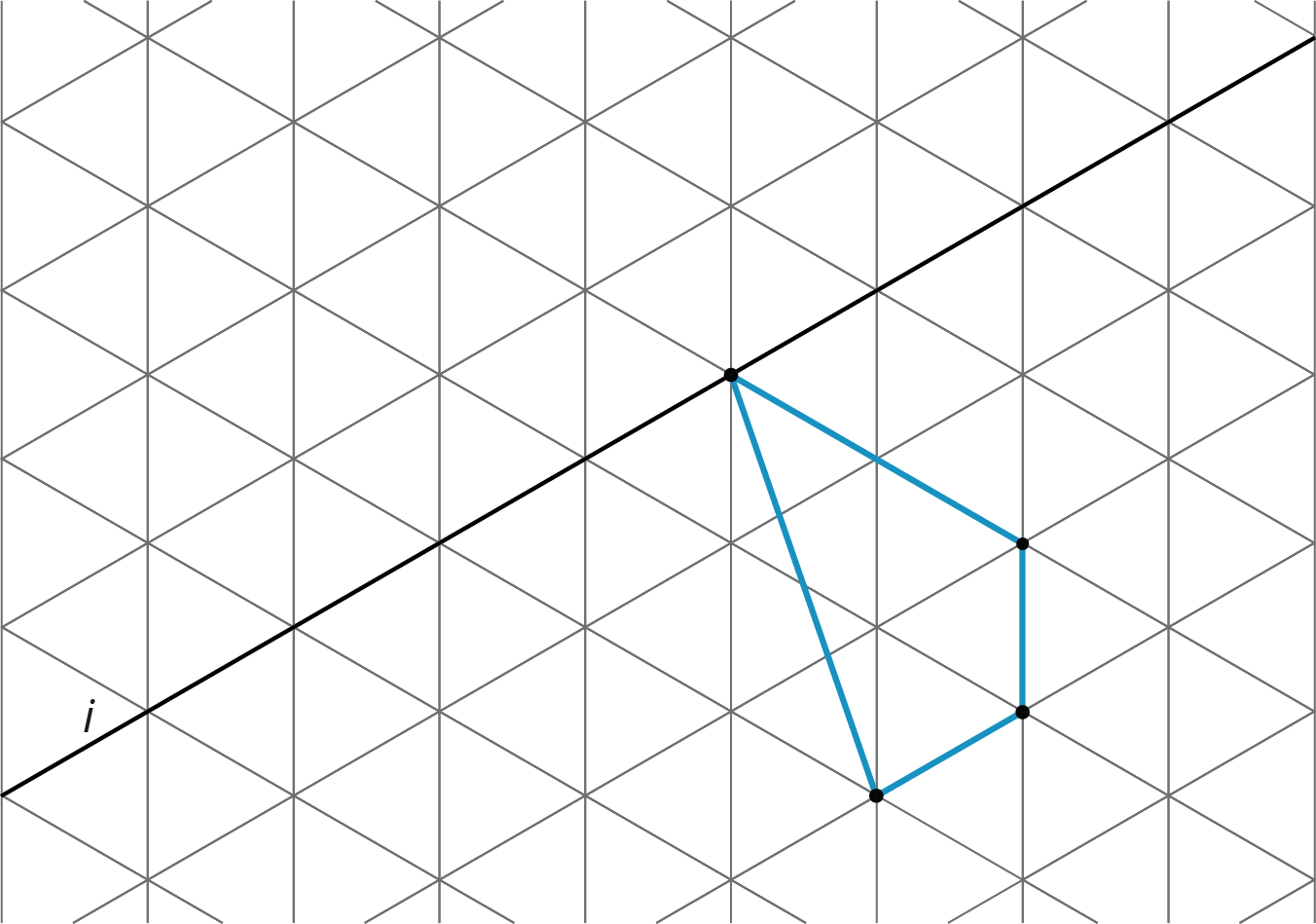
Quadrilateral with one point on line j on a triangular grid.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 4.)