Lesson 6

Describing Transformations

Let’s transform some polygons in the coordinate plane.

6.1: Finding a Center of Rotation

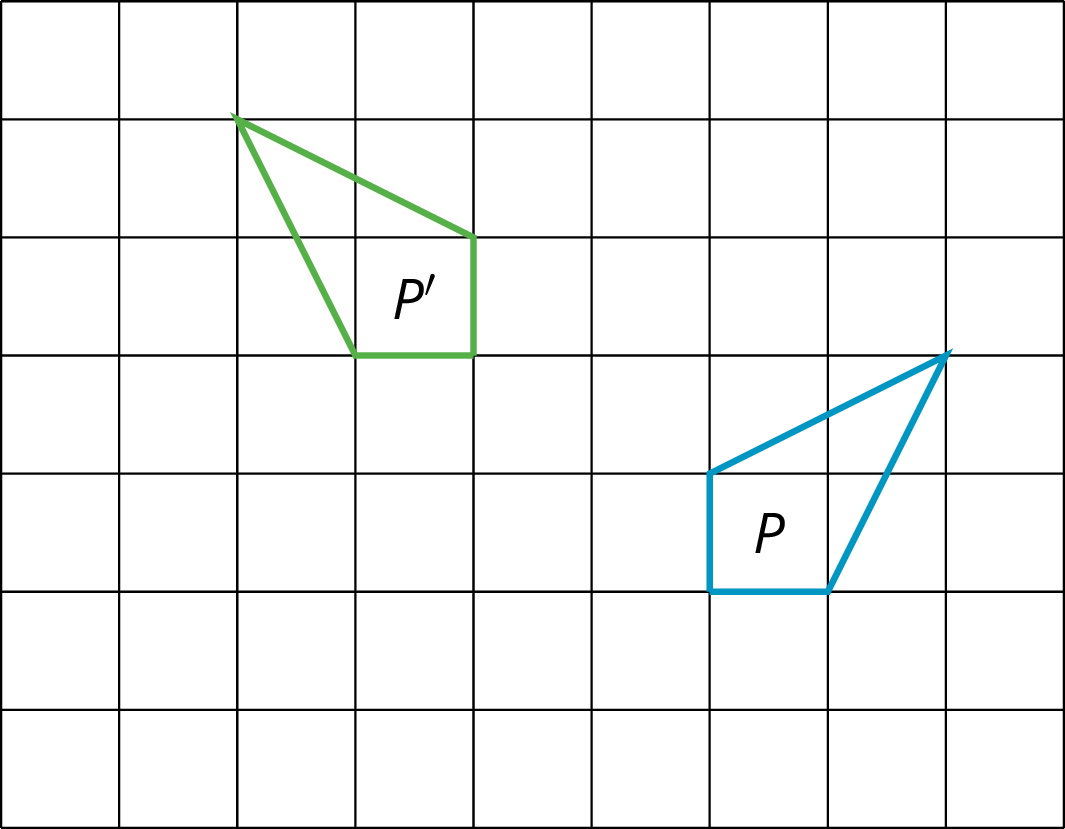
Andre performs a 90-degree counterclockwise rotation of Polygon P and gets Polygon P’, but he does not say what the center of the rotation is. Can you find the center?

Two identical polygons labeled P and P prime on a square grid

 

6.2: Info Gap: Transformation Information

Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.

If your teacher gives you the problem card:

  1. Silently read your card and think about what information you need to be able to answer the question.

  2. Ask your partner for the specific information that you need.

  3. Explain how you are using the information to solve the problem.

    Continue to ask questions until you have enough information to solve the problem.

  4. Share the problem card and solve the problem independently.

  5. Read the data card and discuss your reasoning.

If your teacher gives you the data card:

  1. Silently read your card.

  2. Ask your partner “What specific information do you need?” and wait for them to ask for information.

    If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.

  3. Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.

  4. Read the problem card and solve the problem independently.

  5. Share the data card and discuss your reasoning.

Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.



Sometimes two transformations, one performed after the other, have a nice description as a single transformation. For example, instead of translating 2 units up followed by translating 3 units up, we could simply translate 5 units up. Instead of rotating 20 degrees counterclockwise around the origin followed by rotating 80 degrees clockwise around the origin, we could simply rotate 60 degrees clockwise around the origin.

Can you find a simple description of reflecting across the \(x\)-axis followed by reflecting across the \(y\)-axis?

Summary

The center of a rotation for a figure doesn’t have to be one of the points on the figure. To find a center of rotation, look for a point that is the same distance from two corresponding points. You will probably have to do this for a couple of different pairs of corresponding points to nail it down.

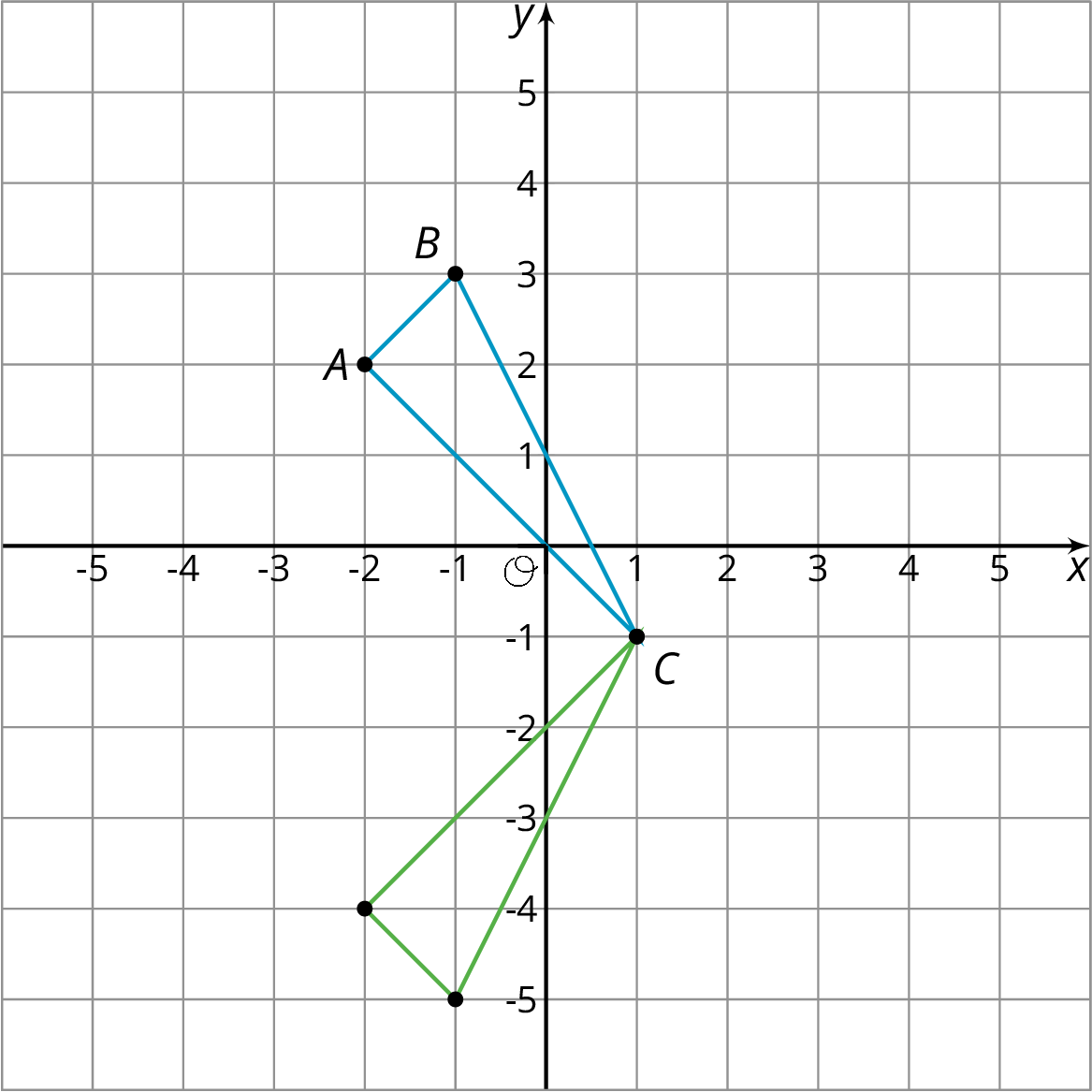
When we perform a sequence of transformations, the order of the transformations can be important. Here is triangle \(ABC\) translated up two units and then reflected over the \(x\)-axis.

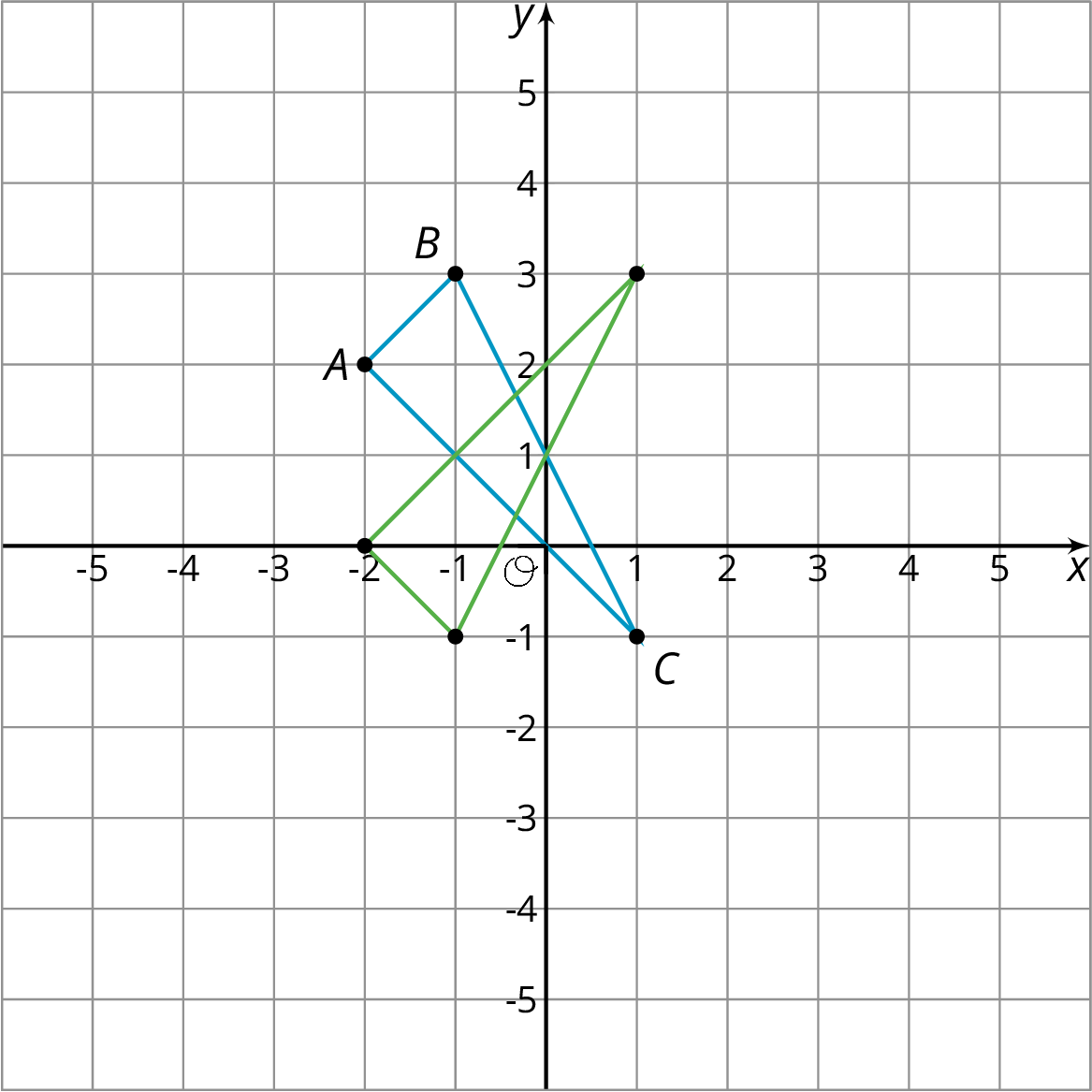
Triangle A B C reflected on a coordinate plane, origin O.

 

Here is triangle \(ABC\) reflected over the \(x\)-axis and then translated up two units.

Triangle \(ABC\) ends up in different places when the transformations are applied in the opposite order!

Triangle A B C reflected on a coordinate plane, origin O.

Video Summary

Video VLS G8U1V1 Rigid Transformations (Lessons 1–6) available at https://player.vimeo.com/video/439303649.

Glossary Entries

  • clockwise

    Clockwise means to turn in the same direction as the hands of a clock. The top turns to the right. This diagram shows Figure A turned clockwise to make Figure B.

  • coordinate plane

    The coordinate plane is a system for telling where points are. For example. point \(R\) is located at \((3, 2)\) on the coordinate plane, because it is three units to the right and two units up.

    Point \(R\) on a coordinate plane, origin \(O\). Horizontal and vertical axis scale negative 4 to 4 by 1’s. The point has coordinates \(R\)(3 comma 2).
  • counterclockwise

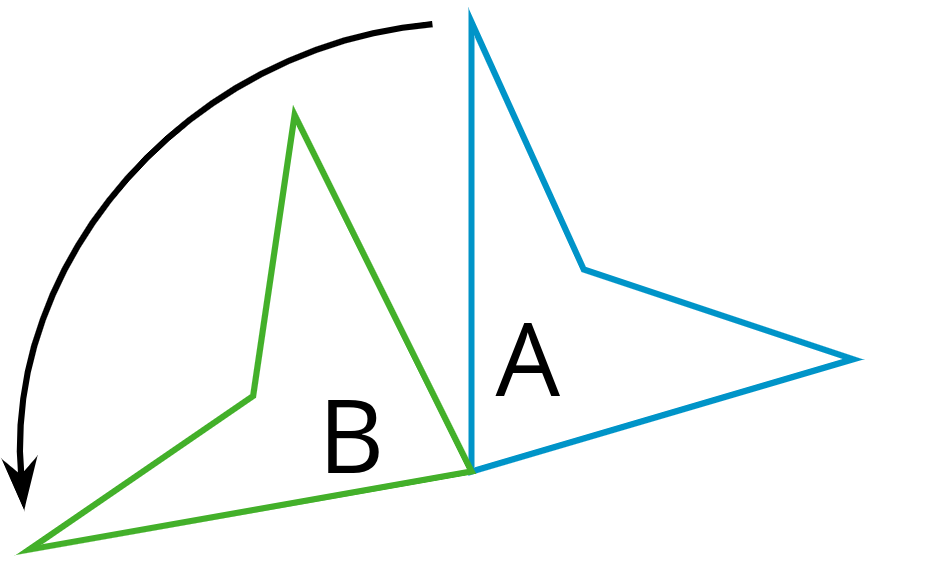
    Counterclockwise means to turn opposite of the way the hands of a clock turn. The top turns to the left.

    This diagram shows Figure A turned counterclockwise to make Figure B.

    Two figures. Figure A turned counterclockwise makes Figure B.

     

  • image

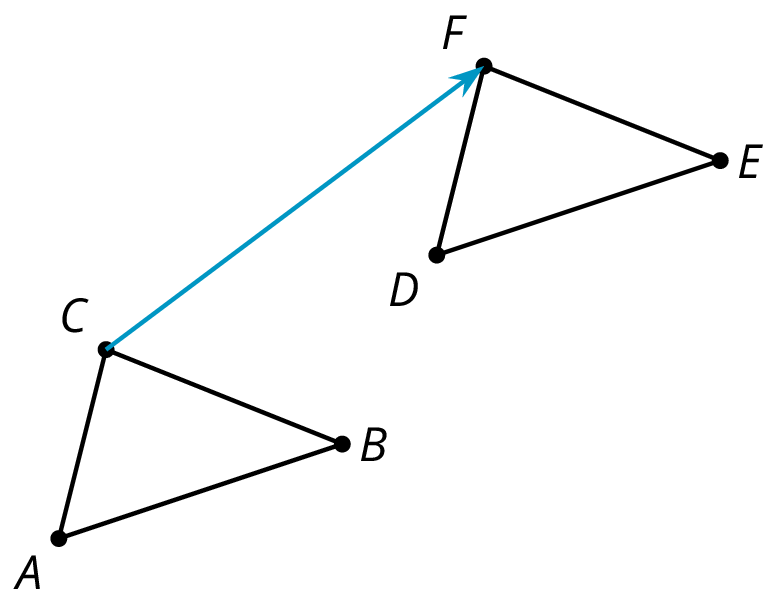
    An image is the result of translations, rotations, and reflections on an object. Every part of the original object moves in the same way to match up with a part of the image.

    In this diagram, triangle \(ABC\) has been translated up and to the right to make triangle \(DEF\). Triangle \(DEF\) is the image of the original triangle \(ABC\).

    2 triangles, ABC and DEF. Triangle ABC has been translated up and to the right to make triangle DEF. Triangle DEF is the image of the original triangle ABC.
  • reflection

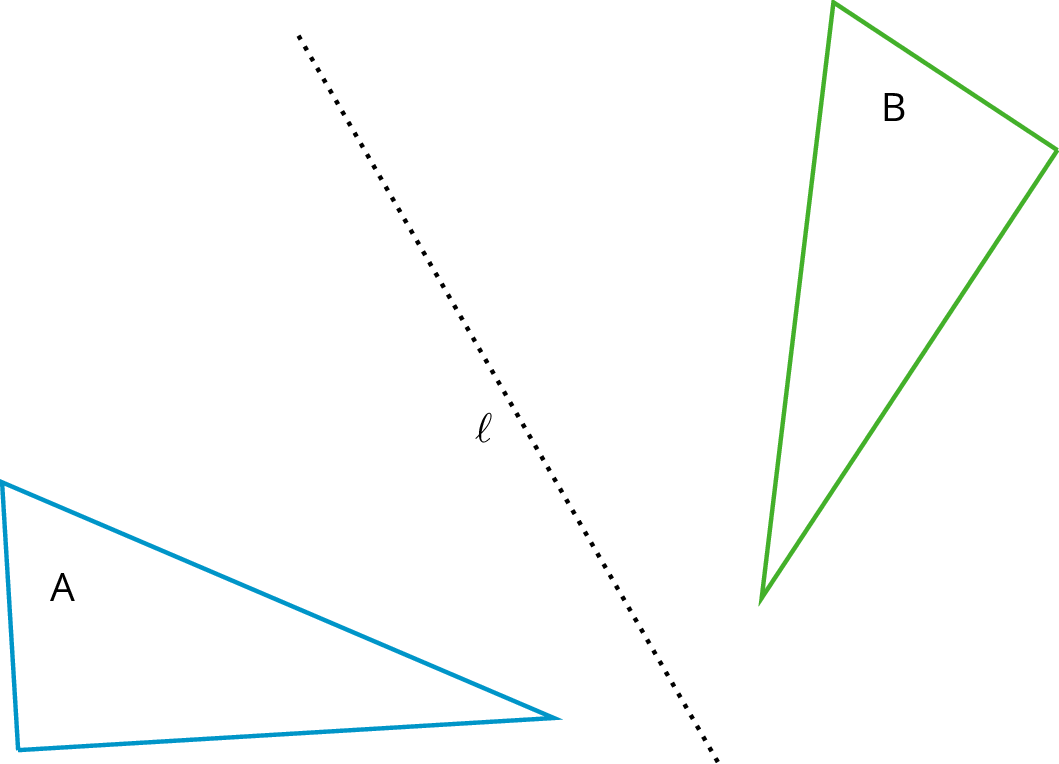
    A reflection across a line moves every point on a figure to a point directly on the opposite side of the line. The new point is the same distance from the line as it was in the original figure.

    This diagram shows a reflection of A over line \(\ell\) that makes the mirror image B.

    Two triangles, A and B. A reflection of A over a line makes the mirror image B.
  • rotation

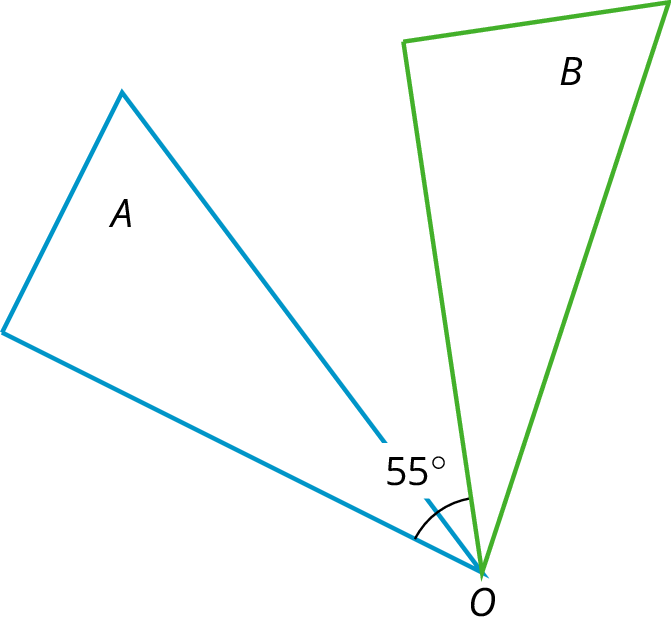
    A rotation moves every point on a figure around a center by a given angle in a specific direction.

    This diagram shows Triangle A rotated around center \(O\) by 55 degrees clockwise to get Triangle B.

    Two trianges, A and B. Triangle A rotated by 55 degrees clockwise gets Triangle B.
  • sequence of transformations

    A sequence of transformations is a set of translations, rotations, reflections, and dilations on a figure. The transformations are performed in a given order.

    This diagram shows a sequence of transformations to move Figure A to Figure C. 

    First, A is translated to the right to make B. Next, B is reflected across line \(\ell\) to make C.

    Transformation taking figure A to figure B.
  • transformation

    A transformation is a translation, rotation, reflection, or dilation, or a combination of these.

  • translation

    A translation moves every point in a figure a given distance in a given direction.

    This diagram shows a translation of Figure A to Figure B using the direction and distance given by the arrow.

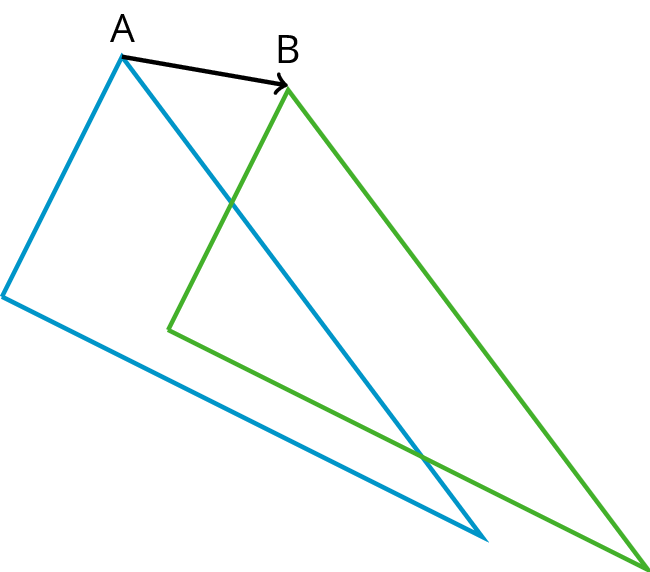
    A translation of triangle A to triangle B
  • vertex

    A vertex is a point where two or more edges meet. When we have more than one vertex, we call them vertices.

    The vertices in this polygon are labeled \(A\), \(B\), \(C\), \(D\), and \(E\).

    Polygon with 5 sides