Lesson 3
Grid Moves
Lesson Narrative
Prior to this lesson, students have learned the names for the basic moves (translation, rotation, and reflection) and have learned how to identify them in pictures. In this lesson, they apply translations, rotations, and reflections to figures. They also label the image of a point \(P\) as \(P'\). While not essential, this practice helps show the structural relationship (MP7) between a figure and its image.
Students also encounter the isometric grid (one made of equilateral triangles with 6 meeting at each vertex). They perform translations, rotations, and reflections both on a square grid and on an isometric grid. Expect a variety of approaches, mainly making use of tracing paper (MP5) but students may also begin to notice how the structure of the different grids helps draw images resulting from certain moves (MP7).
For classrooms using the digital version of the materials: This is the lesson where students learn to use the transformation tools in Geogebra.
Learning Goals
Teacher Facing
- Describe (orally) the moves needed to perform a transformation.
- Draw and label the image and “corresponding points” of figures that result from translations, rotations, and reflections.
- Draw the “image” of a figure that results from a translation, rotation, and reflection in square and isometric grids and justify (orally) that the image is a transformation of the original figure.
Student Facing
Let’s transform some figures on grids.
Required Materials
Required Preparation
Make sure students have access to items in their geometry toolkits: tracing paper, graph paper, colored pencils, scissors, ruler, protractor, and an index card to use as a straightedge or to mark right angles.
For classrooms using the print version of the materials: Access to tracing paper is particularly important. Each student will need about 10 small sheets of tracing paper (commercially available "patty paper" is ideal). If using large sheets of tracing paper, such as 8.5 inches by 11 inches, cut each sheet into fourths.
For classrooms using the digital version of the materials: If you have access to extra help from a tech-savvy person, this would be a good day to request their presence in your class.
Learning Targets
Student Facing
- I can decide which type of transformations will work to move one figure to another.
- I can use grids to carry out transformations of figures.
Glossary Entries
-
image
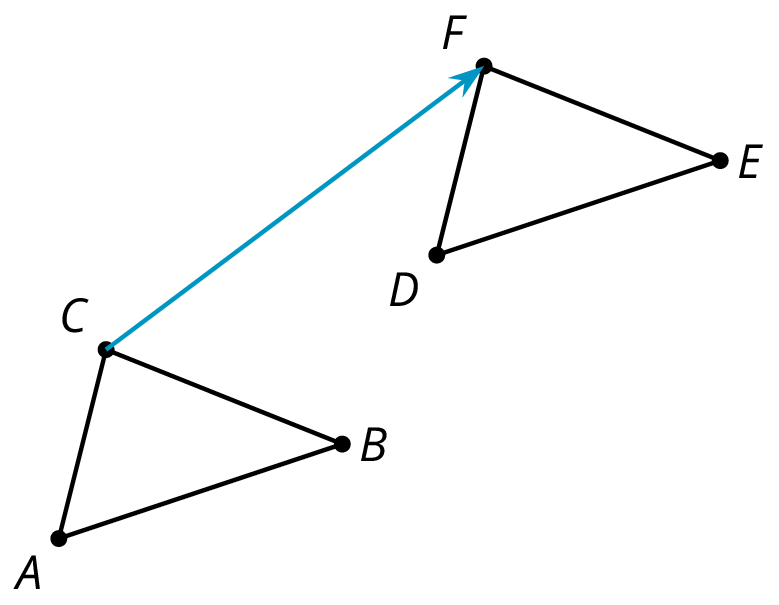
An image is the result of translations, rotations, and reflections on an object. Every part of the original object moves in the same way to match up with a part of the image.
In this diagram, triangle \(ABC\) has been translated up and to the right to make triangle \(DEF\). Triangle \(DEF\) is the image of the original triangle \(ABC\).
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |