Lesson 16
Parallel Lines and the Angles in a Triangle
Lesson Narrative
Earlier in this unit, students learned that when a \(180^\circ\) rotation is applied to a line \(\ell\), the resulting line is parallel to \(\ell\). Here is a picture students worked with earlier in the unit:
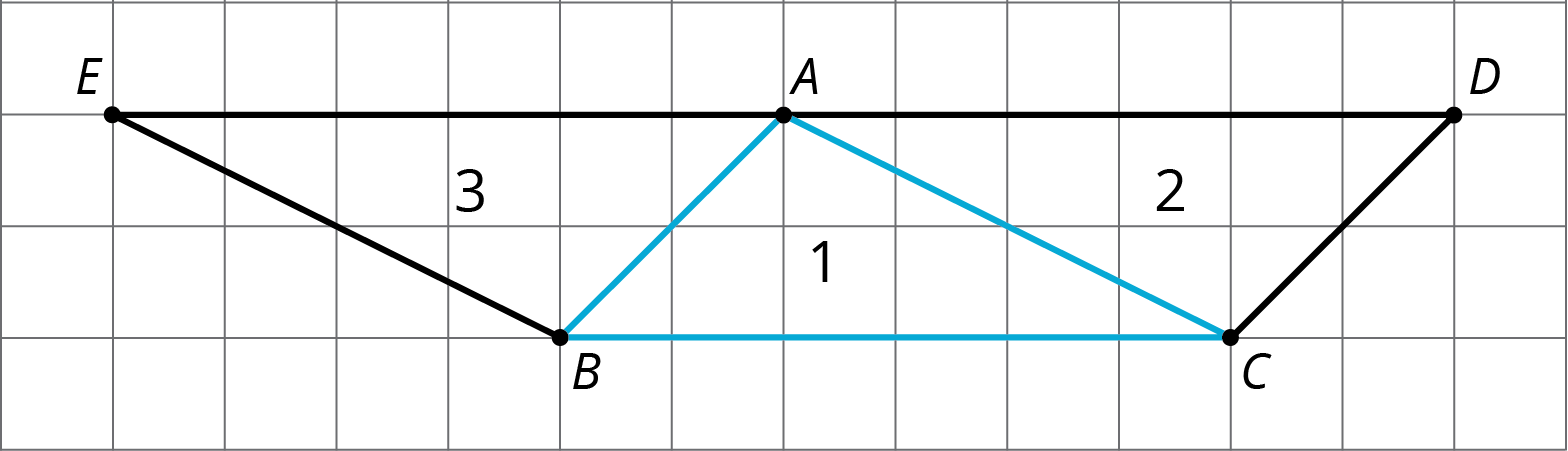
The picture was created by applying \(180^\circ\) rotations to \(\triangle ABC\) with centers at the midpoints of segments \(AC\) and \(AB\). Notice that \(E\), \(A\), and \(D\) all lie on the same grid line that is parallel to line \(BC\). In this case, we have the structure of the grid to help see why this is true. This argument exhibits one aspect of MP7, using the structure of the grid to help explain why the three angles in this triangle add to 180 degrees.
Learning Goals
Teacher Facing
- Create diagrams using 180-degree rotations of triangles to justify (orally and in writing) that the measure of angles in a triangle sum up to 180 degrees.
- Generalize the Triangle Sum Theorem using rigid transformations or the congruence of alternate interior angles of parallel lines cut by a transversal.
Student Facing
Let’s see why the angles in a triangle add to 180 degrees.
Required Materials
Learning Targets
Student Facing
- I can explain using pictures why the sum of the angles in any triangle is 180 degrees.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |