Lesson 12
Congruent Polygons
Lesson Narrative
In this lesson, students find rigid transformations that show two figures are congruent and make arguments for why two figures are not congruent. They learn that, for many shapes, simply having corresponding side lengths that are equal will not guarantee the figures are congruent.
In the previous lesson, students defined what it means for two shapes to be congruent and started to apply the definition to determine if a pair of shapes is congruent. In the first part of this lesson, students continue to determine whether or not pairs of shapes are congruent, but here they have the extra structure of a grid. With this extra structure, students use MP6 (attend to precision) when describing translations, reflections, and rotations. For example:
- Instead of “translate down and to the left,” students can say, “translate 3 units down and 2 units to the left”
- Instead of “reflect the shape,” students can say, “reflect the shape over this vertical line.”
In addition, students have to be careful how they name congruent polygons, making sure that corresponding vertices are listed in the proper order.
An optional part of the lesson begins to examine criteria to decide when two shapes are congruent. If two shapes are congruent, then their corresponding sides and angles are congruent. Is it true that having the same side lengths (or angles) is enough to determine whether or not two shapes are congruent? Students investigate this question for quadrilaterals in two different situations:
- 4 congruent side lengths.
- 2 pairs of congruent side lengths where the pairs are of different length.
Learning Goals
Teacher Facing
- Comprehend that figures with the same area and perimeter may or may not be congruent.
- Critique arguments (orally) that two figures with congruent corresponding sides may be non-congruent figures.
- Justify (orally and in writing) that two polygons on a grid are congruent using the definition of congruence in terms of transformations.
Student Facing
Let’s decide if two figures are congruent.
Required Materials
Required Preparation
If you choose to have students complete the optional activity, have sets of objects ready for students to build quadrilaterals. Each pair of students requires 12 objects (such as toothpicks, pencils, or straws) to be used as sides of quadrilaterals: 8 objects of one length and 4 objects of a different length.
Learning Targets
Student Facing
- I can decide using rigid transformations whether or not two figures are congruent.
CCSS Standards
Addressing
Glossary Entries
-
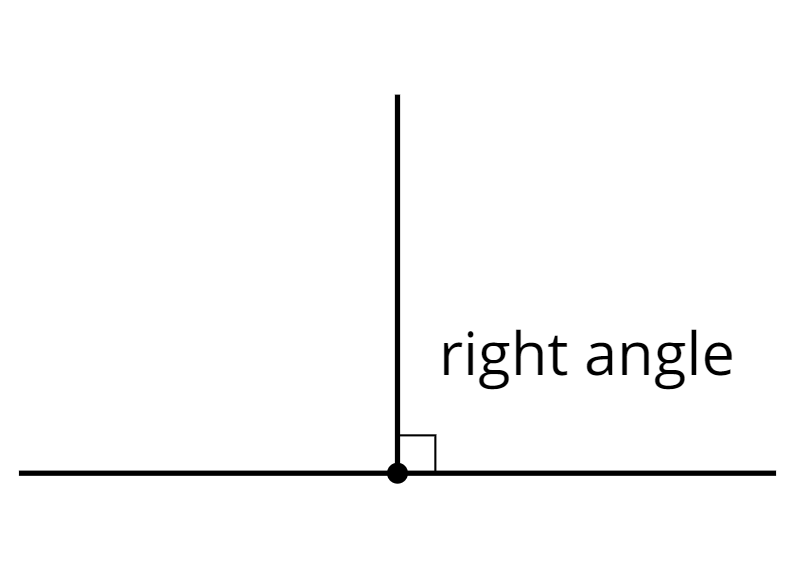
right angle
A right angle is half of a straight angle. It measures 90 degrees.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |