Lesson 3

Nonadjacent Angles

View Student Lesson

Lesson Narrative

In this lesson, students see that angles do not need to be adjacent to be complementary or supplementary. Students are also introduced to and begin to use the term vertical angles for describing the opposite angles formed when two lines cross (MP6). They examine multiple examples and see that the vertical angles have equal measures. Students can relate this understanding to the fact that both angles in a pair of vertical angles are supplementary to the same angle in between, but in grade 7 students do not need to be able to give a formal geometric proof that vertical angles must have equal measures. As students see different ways of making pairs of supplementary angles in two lines crossing, they engage in MP7.


Learning Goals

Teacher Facing

  • Comprehend the term “vertical angles” (in spoken and written language) refers to a pair of angles created by two intersecting lines.
  • Generalize (orally and in writing) that the opposite angles created by two intersecting lines have equal angle measures.
  • Use reasoning about angle measures to identify complementary or supplementary angles that are not adjacent.

Student Facing

Let’s look at angles that are not right next to one another.

Required Materials

Learning Targets

Student Facing

  • I can determine if angles that are not adjacent are complementary or supplementary.
  • I can explain what vertical angles are in my own words.

CCSS Standards

Addressing

Glossary Entries

  • vertical angles

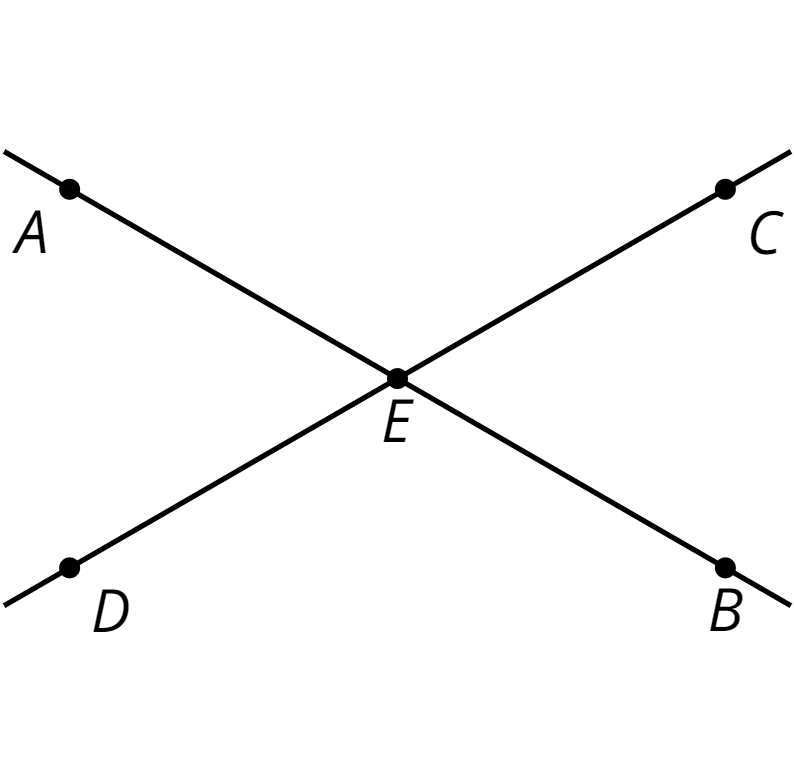
    Vertical angles are opposite angles that share the same vertex. They are formed by a pair of intersecting lines. Their angle measures are equal.

    For example, angles \(AEC\) and \(DEB\) are vertical angles. If angle \(AEC\) measures \(120^\circ\), then angle \(DEB\) must also measure \(120^\circ\).

    Angles \(AED\) and \(BEC\) are another pair of vertical angles.

    a pair of intersecting lines that create vertical angles

Print Formatted Materials

For access, consult one of our IM Certified Partners.

Additional Resources

Google Slides

For access, consult one of our IM Certified Partners.
PowerPoint Slides

For access, consult one of our IM Certified Partners.