Lesson 2
Finding Area by Decomposing and Rearranging
Let’s create shapes and find their areas.
Problem 1
The diagonal of a rectangle is shown.

-
Decompose the rectangle along the diagonal, and recompose the two pieces to make a different shape.
-
How does the area of this new shape compare to the area of the original rectangle? Explain how you know.
Problem 2
Priya decomposed a square into 16 smaller, equal-size squares and then cut out 4 of the small squares and attached them around the outside of original square to make a new figure.
How does the area of her new figure compare with that of the original square?
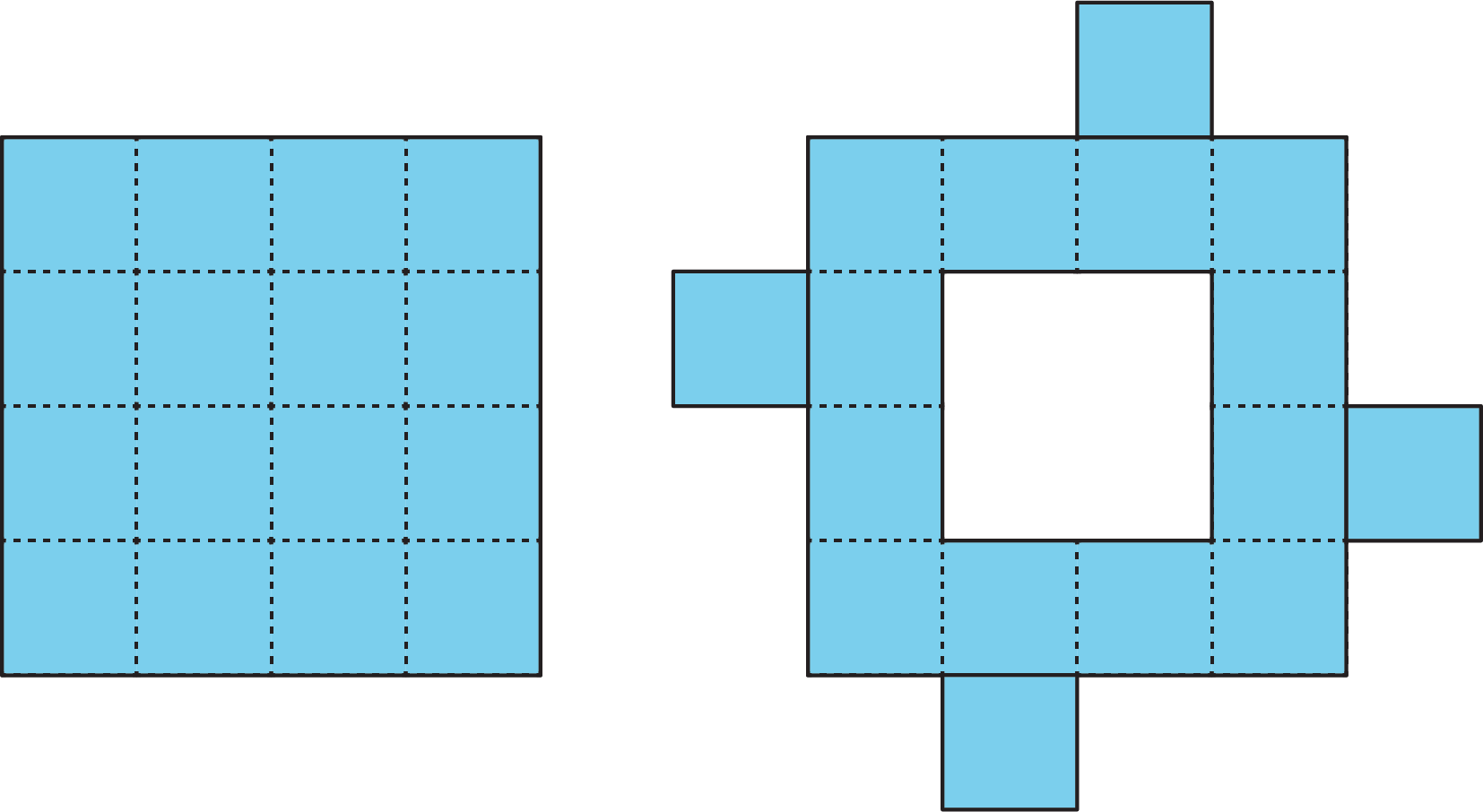
The area of the new figure is greater.
The two figures have the same area.
The area of the original square is greater.
We don’t know because neither the side length nor the area of the original square is known.
Problem 3
The area of the square is 1 square unit. Two small triangles can be put together to make a square or to make a medium triangle.
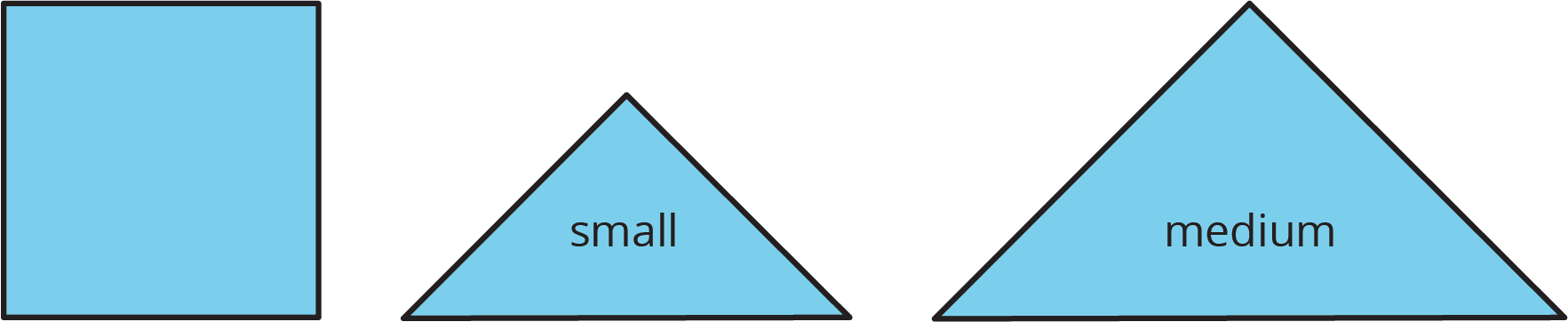
Which figure also has an area of \(1\frac 12\) square units? Select all that apply.

Figure A
Figure B
Figure C
Figure D
Problem 4
The area of a rectangular playground is 78 square meters. If the length of the playground is 13 meters, what is its width?
Problem 5
A student said, “We can’t find the area of the shaded region because the shape has many different measurements, instead of just a length and a width that we could multiply.”

Explain why the student’s statement about area is incorrect.