Lesson 6
Area of Parallelograms
Let's practice finding the area of parallelograms.
6.1: Missing Dots

How many dots are in the image?
How do you see them?
6.2: More Areas of Parallelograms
-
-
Calculate the area of the given figure in the applet. Then, check if your area calculation is correct by clicking the Show Area checkbox.
- Uncheck the Area checkbox. Move one of the vertices of the parallelogram to create a new parallelogram. When you get a parallelogram that you like, sketch it and calculate the area. Then, check if your calculation is correct by using the Show Area button again.
- Repeat this process two more times. Draw and label each parallelogram with its measurements and the area you calculated.
-
- Here is Parallelogram B. What is the corresponding height for the base that is 10 cm long? Explain or show your reasoning.
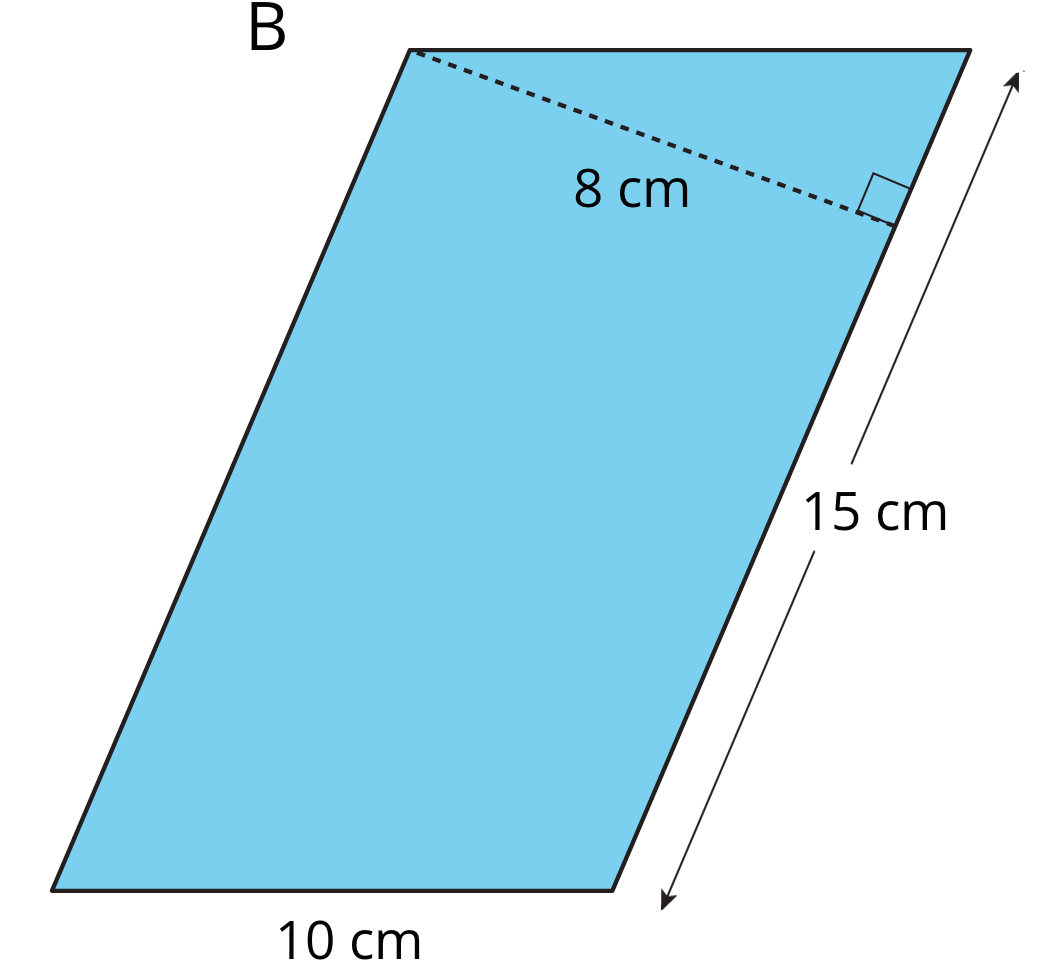
-
Here are two different parallelograms with the same area.
- Explain why their areas are equal.
- Drag points to create two new parallelograms that are not identical copies of each other but that have the same area as each other. Sketch your parallelograms and explain or show how you know their areas are equal. Then, click on the Check button to see if the two areas are indeed equal.
Here is a parallelogram composed of smaller parallelograms. The shaded region is composed of four identical parallelograms. All lengths are in inches.
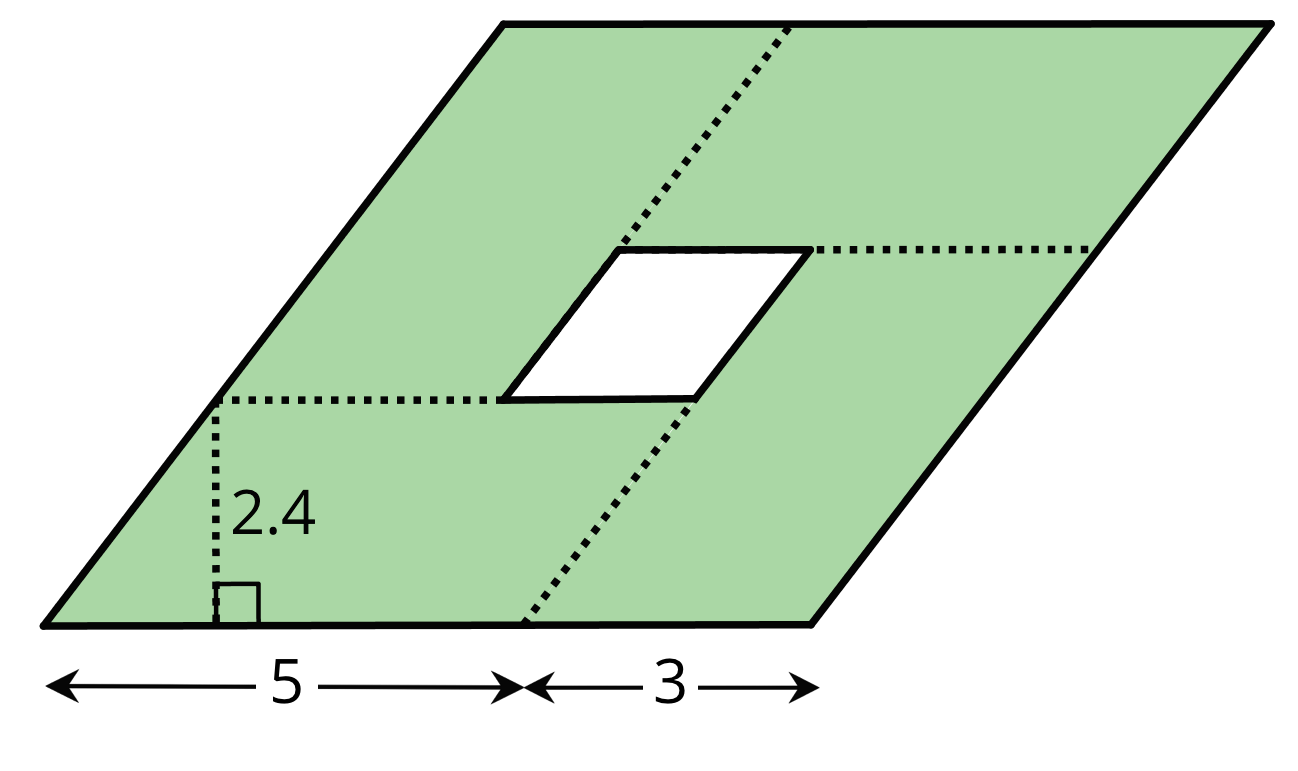
What is the area of the unshaded parallelogram in the middle? Explain or show your reasoning.
Summary
Any pair of base and corresponding height can help us find the area of a parallelogram, but some base-height pairs are more easily identified than others.
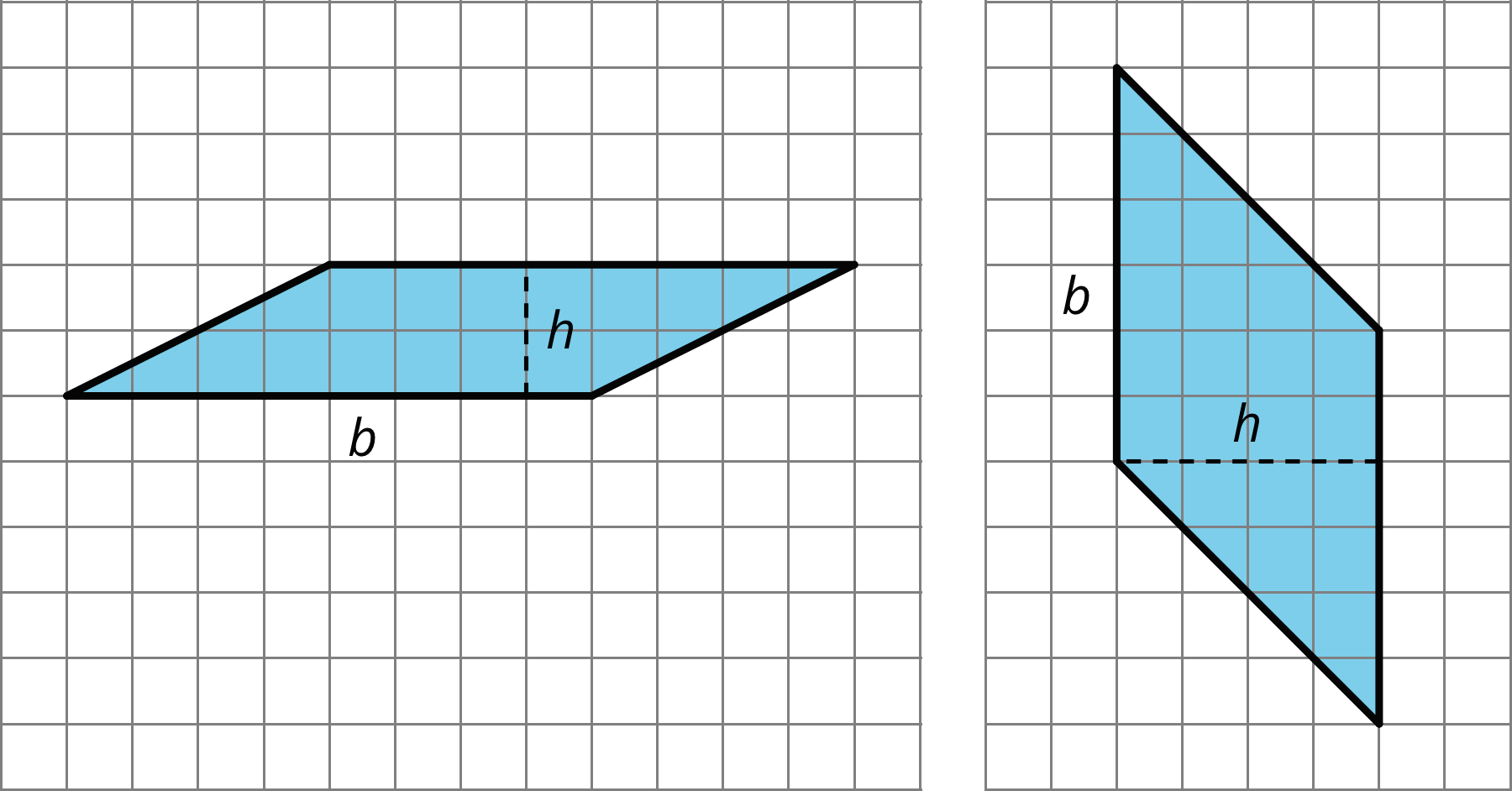
When a parallelogram is drawn on a grid and has horizontal sides, we can use a horizontal side as the base. When it has vertical sides, we can use a vertical side as the base. The grid can help us find (or estimate) the lengths of the base and of the corresponding height.
When a parallelogram is not drawn on a grid, we can still find its area if a base and a corresponding height are known.
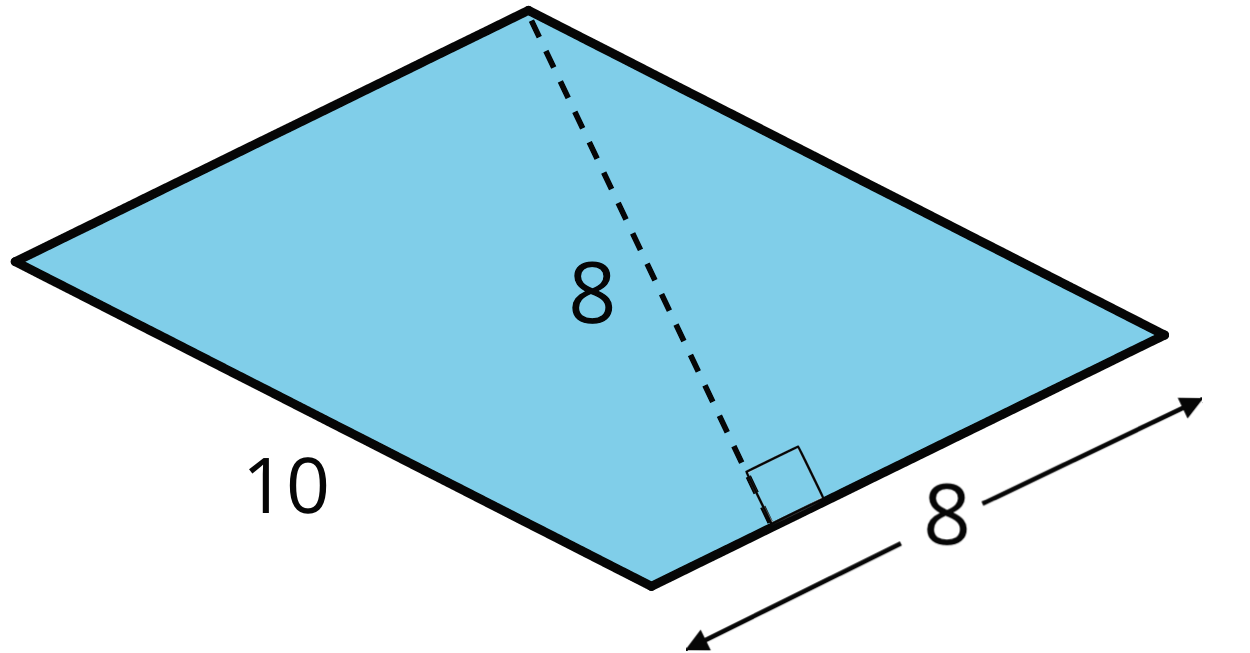
In this parallelogram, the corresponding height for the side that is 10 units long is not given, but the height for the side that is 8 units long is given. This base-height pair can help us find the area.
Regardless of their shape, parallelograms that have the same base and the same height will have the same area; the product of the base and height will be equal. Here are some parallelograms with the same pair of base-height measurements.

Video Summary
Glossary Entries
- base (of a parallelogram or triangle)
We can choose any side of a parallelogram or triangle to be the shape’s base. Sometimes we use the word base to refer to the length of this side.
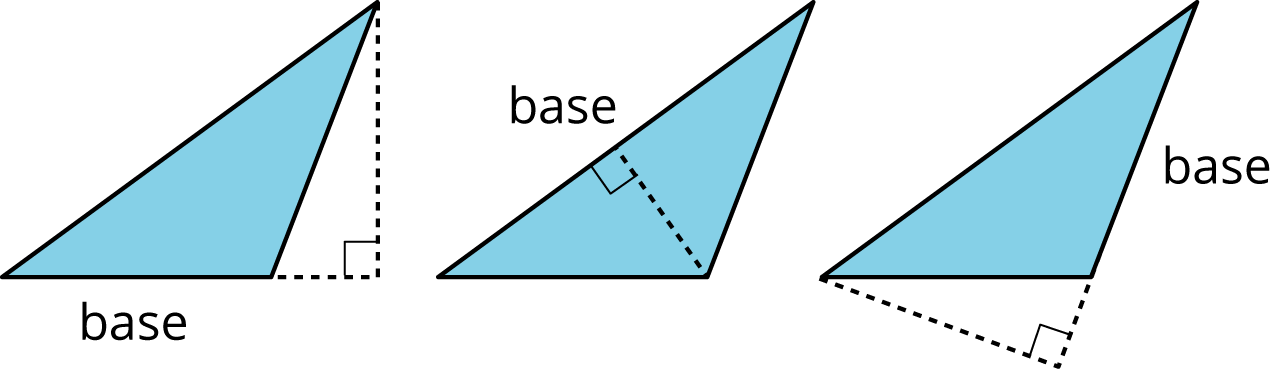
- height (of a parallelogram or triangle)
The height is the shortest distance from the base of the shape to the opposite side (for a parallelogram) or opposite vertex (for a triangle).
We can show the height in more than one place, but it will always be perpendicular to the chosen base.

- parallelogram
A parallelogram is a type of quadrilateral that has two pairs of parallel sides.
Here are two examples of parallelograms.

- quadrilateral
A quadrilateral is a type of polygon that has 4 sides. A rectangle is an example of a quadrilateral. A pentagon is not a quadrilateral, because it has 5 sides.