Lesson 16

Distinguishing Between Surface Area and Volume

Let’s contrast surface area and volume.

16.1: Attributes and Their Measures

For each quantity, choose one or more appropriate units of measurement.

For the last two, think of a quantity that could be appropriately measured with the given units.

Quantities

  1. Perimeter of a parking lot:
  2. Volume of a semi truck:
  3. Surface area of a refrigerator:
  4. Length of an eyelash:
  5. Area of a state:
  6. Volume of an ocean:
  7. ________________________: miles
  8. ________________________: cubic meters

Units

  • millimeters (mm)
  • feet (ft)
  • meters (m)
  • square inches (sq in)
  • square feet (sq ft)
  • square miles (sq mi)
  • cubic kilometers (cu km)
  • cubic yards (cu yd)

16.2: Building with 8 Cubes

This applet has 16 cubes in its hidden stack. Build two different shapes using 8 cubes for each.

For each shape, determine the following information and write it on a sticky note.

  • Give a name or a label (e.g., Mae’s First Shape or Eric’s Steps).
  • Determine its volume.
  • Determine its surface area.

16.3: Comparing Prisms Without Building Them

Three rectangular prisms each have a height of 1 cm.

  • Prism A has a base that is 1 cm by 11 cm.
  • Prism B has a base that is 2 cm by 7 cm.
  • Prism C has a base that is 3 cm by 5 cm.

  1. Find the surface area and volume of each prism. Use the dot paper to draw the prisms, if needed.

    isometric dot paper
  2. Analyze the volumes and surface areas of the prisms. What do you notice? Write 1 or 2 observations about them.


Can you find more examples of prisms that have the same surface areas but different volumes? How many can you find?

Summary

Length is a one-dimensional attribute of a geometric figure. We measure lengths using units like millimeters, centimeters, meters, kilometers, inches, feet, yards, and miles.

pencil with ruler along length

Area is a two-dimensional attribute. We measure area in square units. For example, a square that is 1 centimeter on each side has an area of 1 square centimeter.

Rectangular widow with rulers along the length and width

Volume is a three-dimensional attribute. We measure volume in cubic units. For example, a cube that is 1 kilometer on each side has a volume of 1 cubic kilometer.

3 boxes stacked vertically, rulers along length, width, and height

Surface area and volume are different attributes of three-dimensional figures. Surface area is a two-dimensional measure, while volume is a three-dimensional measure.

Two figures can have the same volume but different surface areas. For example:

  • A rectangular prism with side lengths of 1 cm, 2 cm, and 2 cm has a volume of 4 cu cm and a surface area of 16 sq cm.
  • A rectangular prism with side lengths of 1 cm, 1 cm, and 4 cm has the same volume but a surface area of 18 sq cm.
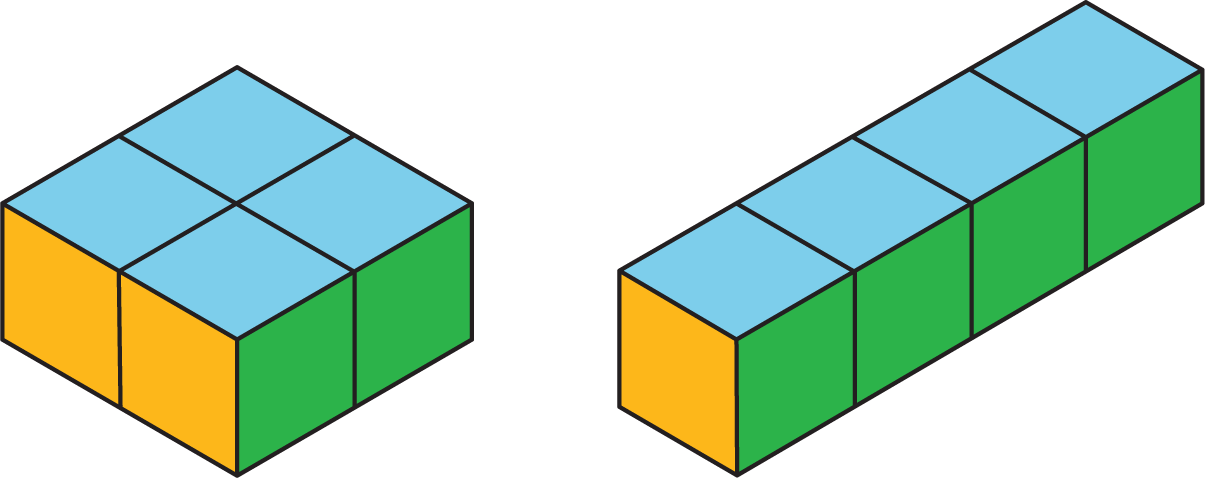
4 cubes arranged into two different rectangular prisms

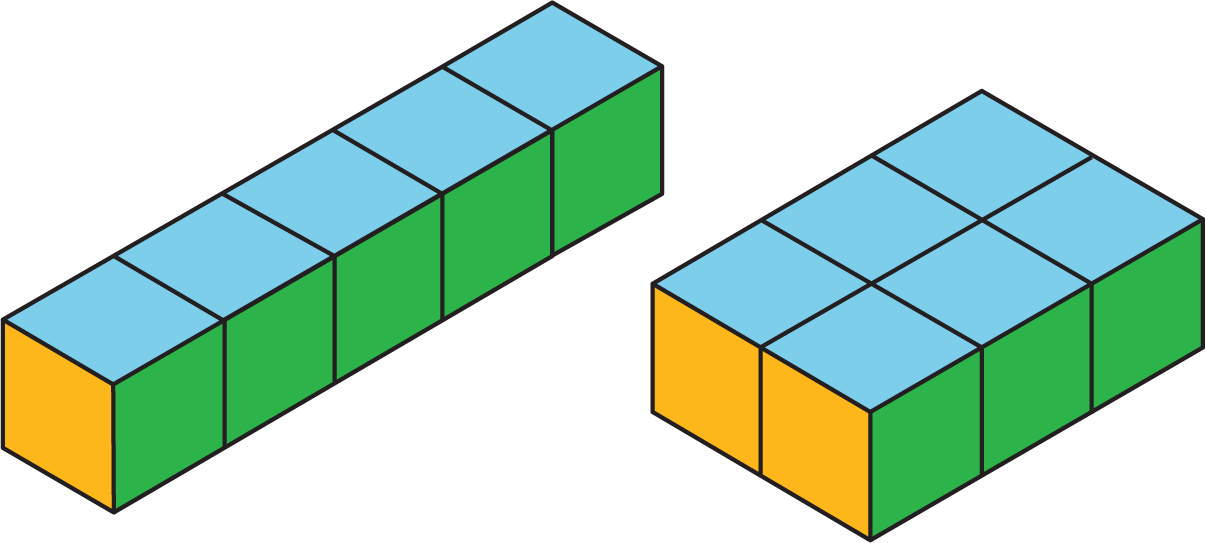
Similarly, two figures can have the same surface area but different volumes. 

  • A rectangular prism with side lengths of 1 cm, 1 cm, and 5 cm has a surface area of 22 sq cm and a volume of 5 cu cm.
  • A rectangular prism with side lengths of 1 cm, 2 cm, and 3 cm has the same surface area but a volume of 6 cu cm.
2 different rectangular prisms

Glossary Entries

  • base (of a prism or pyramid)

    The word base can also refer to a face of a polyhedron.

    A prism has two identical bases that are parallel. A pyramid has one base.

    A prism or pyramid is named for the shape of its base.

    Two figures, a pentagonal prism and a hexagonal pyramid.
  • face

    Each flat side of a polyhedron is called a face. For example, a cube has 6 faces, and they are all squares.

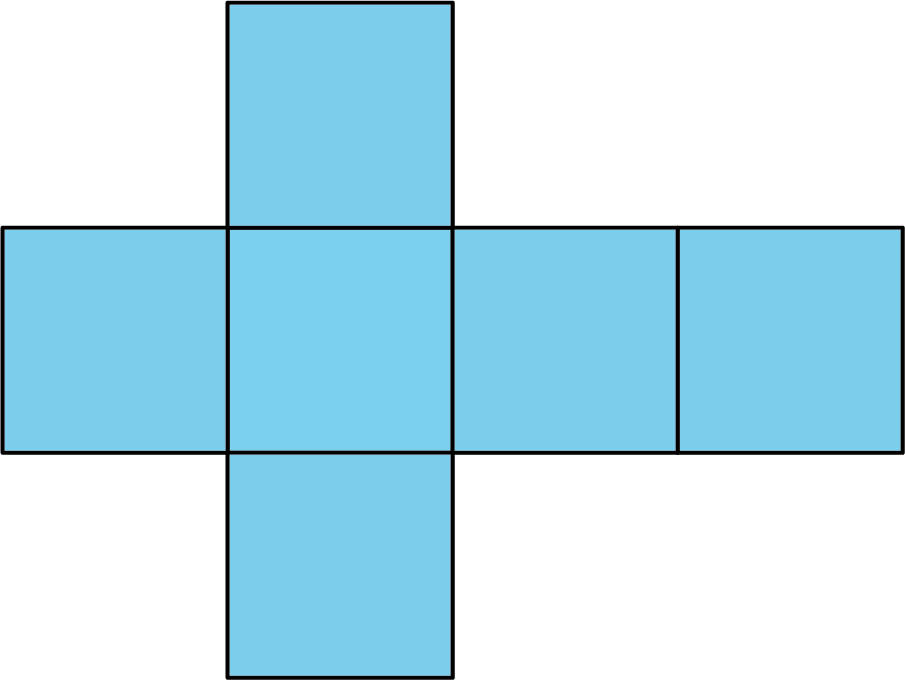
  • net

    A net is a two-dimensional figure that can be folded to make a polyhedron.

    Here is a net for a cube.

    Six squares arranged with 4 in a row, 1 above the second square in the row, and one below the second square in the row.
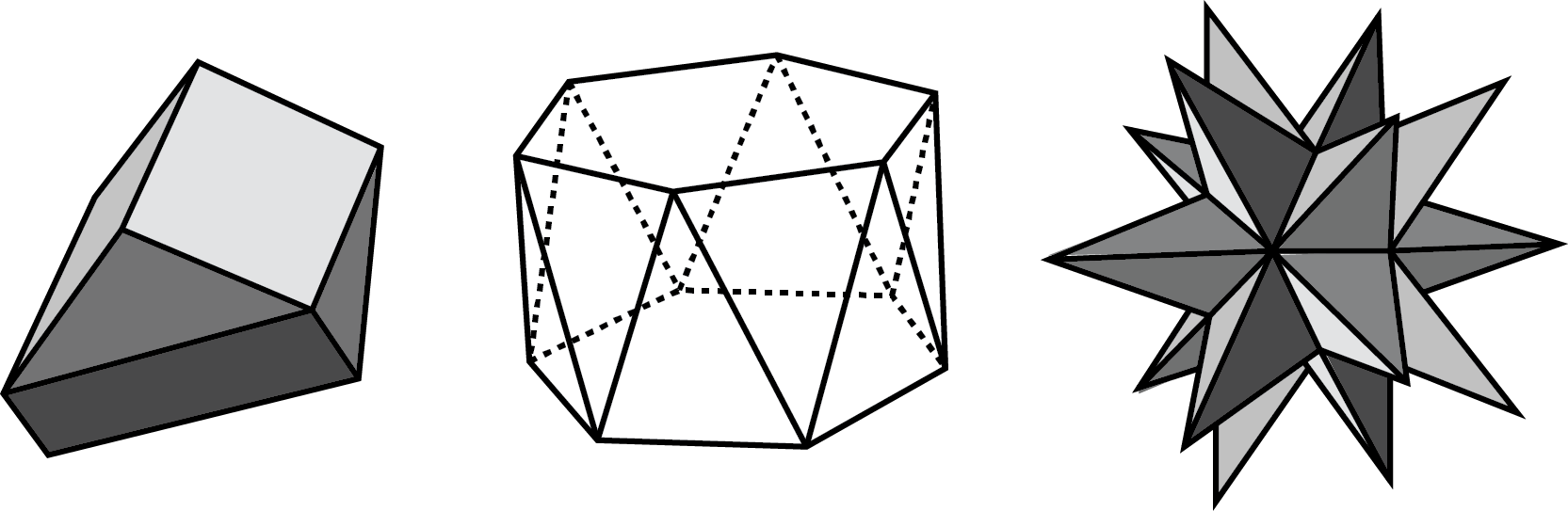
  • polyhedron

    A polyhedron is a closed, three-dimensional shape with flat sides. When we have more than one polyhedron, we call them polyhedra.

    Here are some drawings of polyhedra.

    3 polyhedra, from left to right shapes resemble a house, drum, and star.
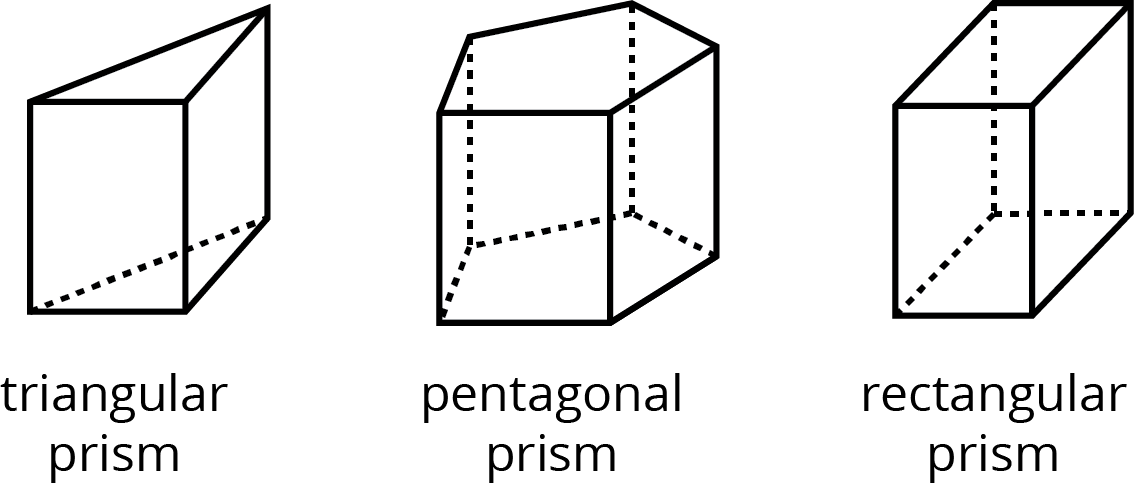
  • prism

    A prism is a type of polyhedron that has two bases that are identical copies of each other. The bases are connected by rectangles or parallelograms.

    Here are some drawings of prisms.

    A triangular prism, a pentagonal prism, and a rectangular prism.
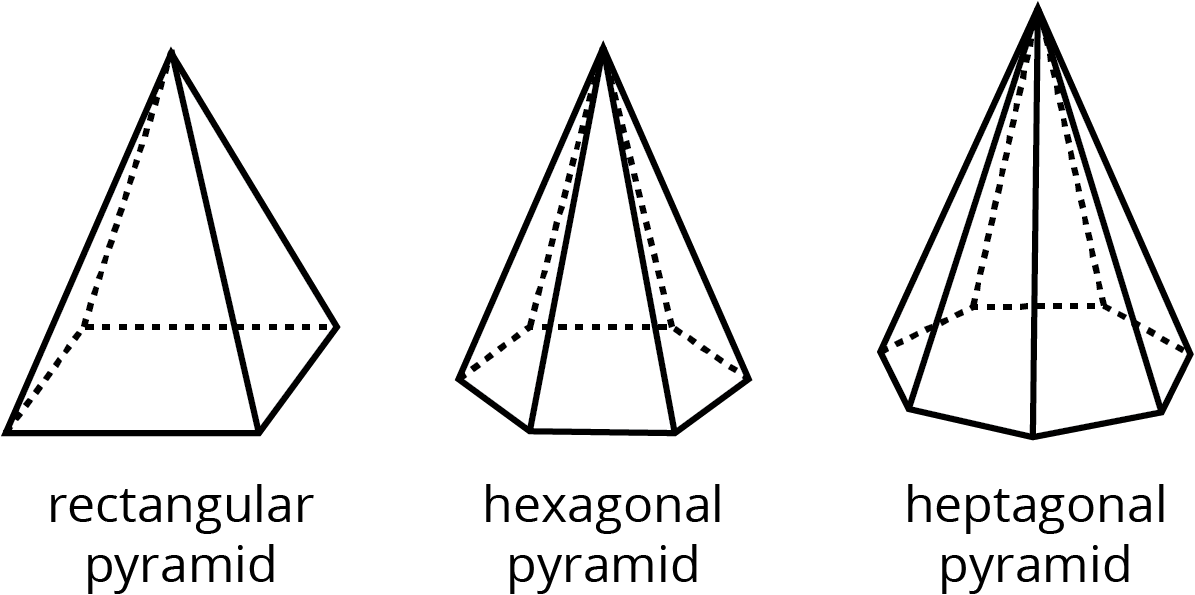
  • pyramid

    A pyramid is a type of polyhedron that has one base. All the other faces are triangles, and they all meet at a single vertex.

    Here are some drawings of pyramids.

    a rectangular pyramid, a hexagonal pyramid, a heptagonal pyramid
  • surface area

    The surface area of a polyhedron is the number of square units that covers all the faces of the polyhedron, without any gaps or overlaps.

    For example, if the faces of a cube each have an area of 9 cm2, then the surface area of the cube is \(6 \boldcdot 9\), or 54 cm2.

  • volume

    Volume is the number of cubic units that fill a three-dimensional region, without any gaps or overlaps.

    For example, the volume of this rectangular prism is 60 units3, because it is composed of 3 layers that are each 20 units3.

    Two images. First, a prism made of cubes stacked 5 wide, 4 deep, 3 tall. Second, each of the layers of the prism is separated to show 3 prisms 5 wide, 4 deep, 1 tall.