Lesson 10
Bases and Heights of Triangles
Let’s use different base-height pairs to find the area of a triangle.
Problem 1
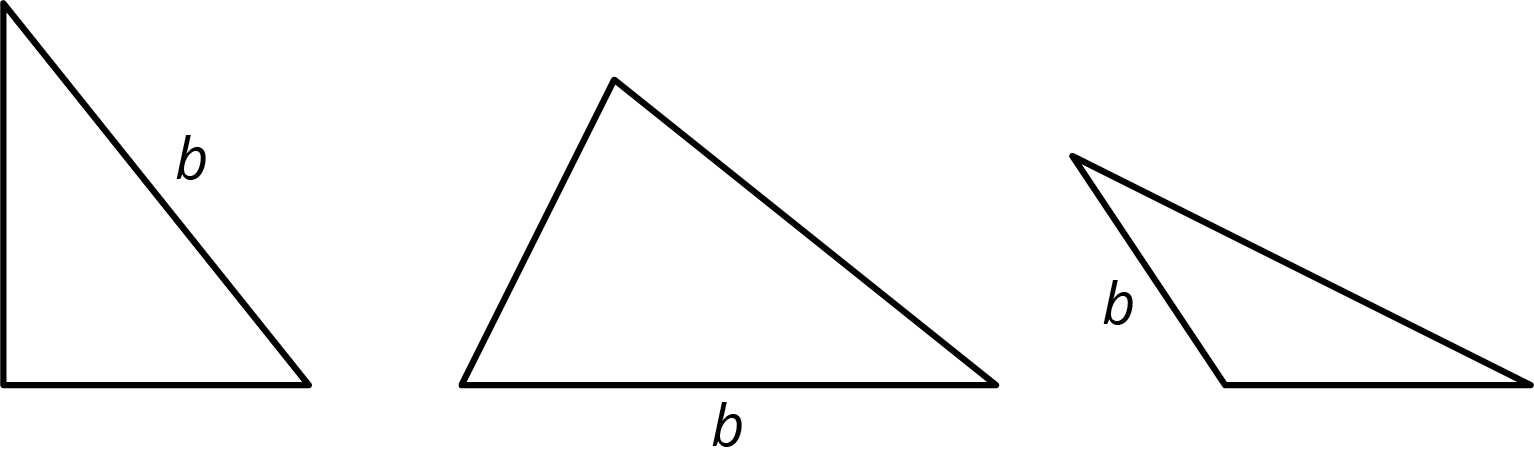
For each triangle, a base is labeled \(b\). Draw a line segment that shows its corresponding height. Use an index card to help you draw a straight line.
Problem 2
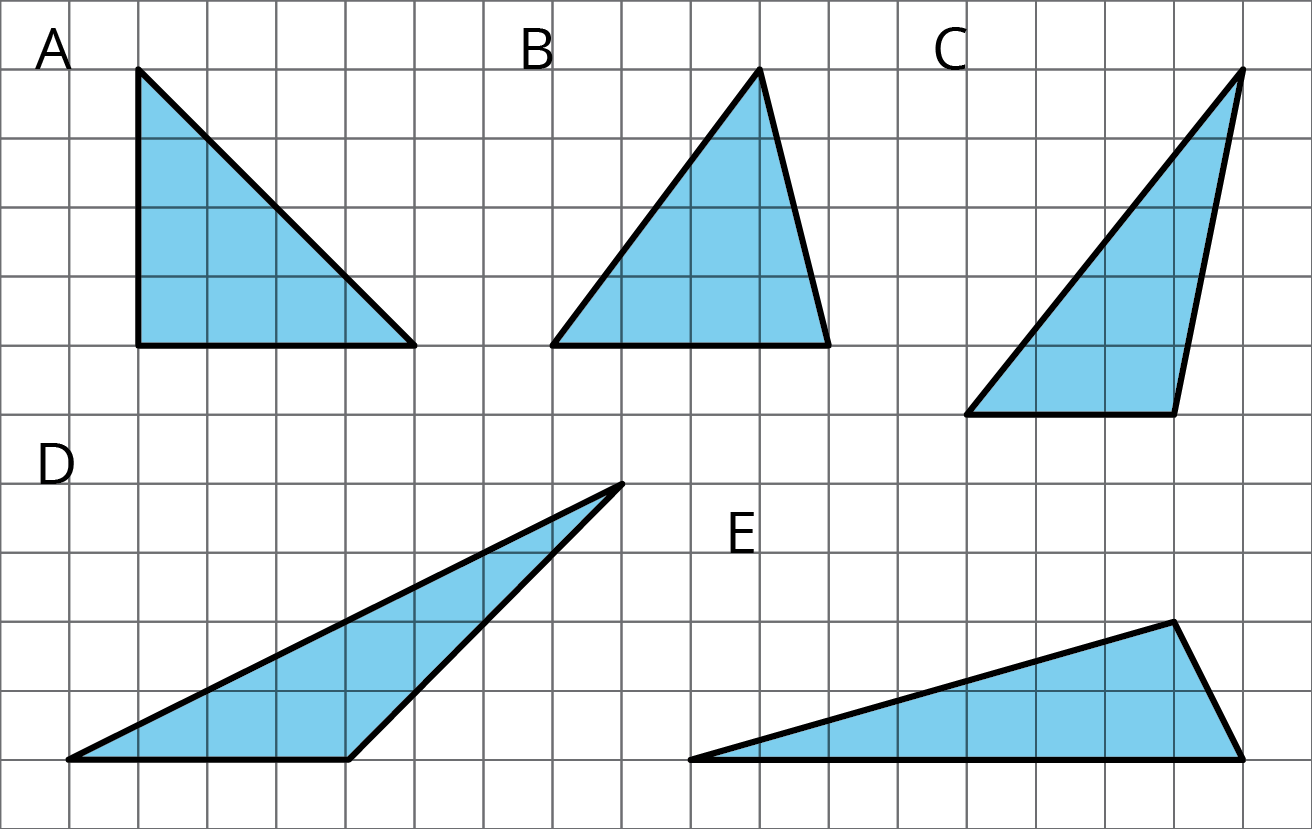
Select all triangles that have an area of 8 square units. Explain how you know.
Problem 3
Find the area of the triangle. Show your reasoning.

If you get stuck, carefully consider which side of the triangle to use as the base.
Problem 4
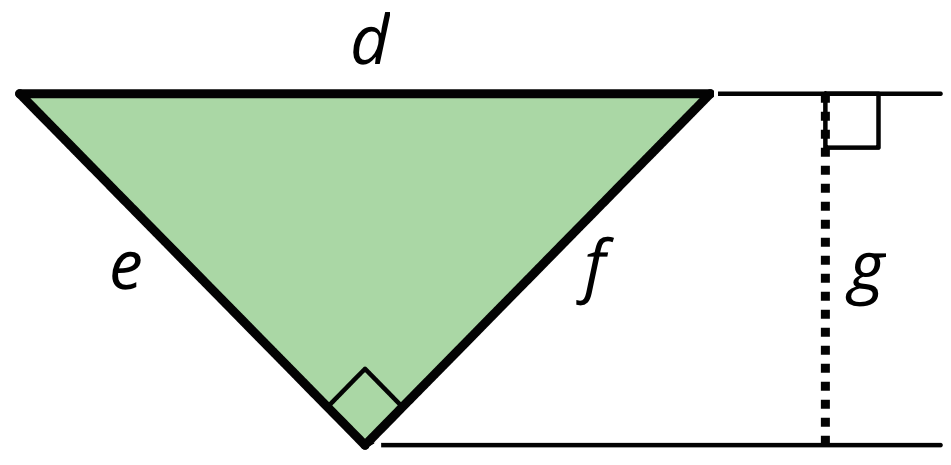
Can side \(d\) be the base for this triangle? If so, which length would be the corresponding height? If not, explain why not.
Problem 5
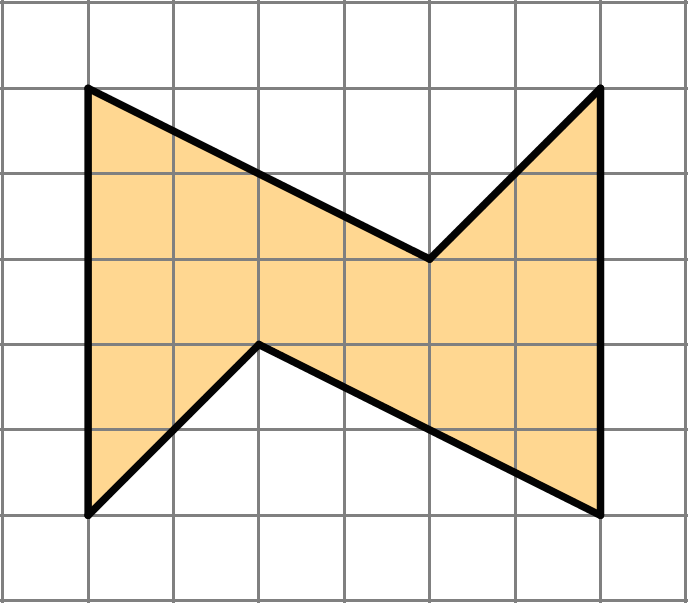
Find the area of this shape. Show your reasoning.
Problem 6
On the grid, sketch two different parallelograms that have equal area. Label a base and height of each and explain how you know the areas are the same.
